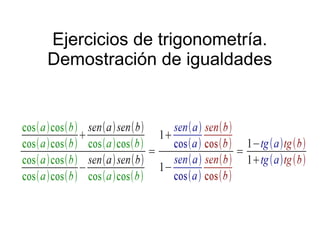
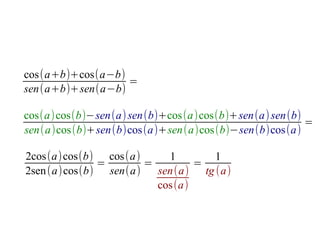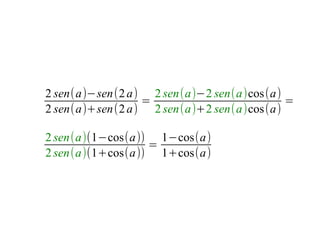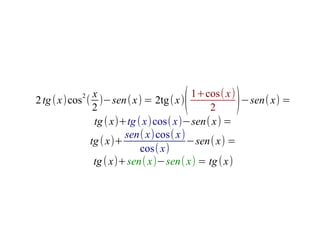Este documento presenta una estrategia para demostrar igualdades trigonométricas complejas mediante el desarrollo de expresiones y la simplificación de términos. Incluye cinco ejemplos resueltos que ilustran esta estrategia, desarrollando expresiones que contienen sumas, restas y ángulos dobles y simplificando los términos resultantes.

1. Ejercicios de trigonometría.
Demostración de igualdades

2. Introducción
La trigonometría de 1º de Bachillerato ofrece
una serie de ejercicios que nos piden
demostrar ciertas expresiones trigonométricas
complejas, siendo un ejercicio adecuado para
el razonamiento simbólico y la elaboración de
demostraciones, frecuentes en las
matemáticas del Bachillerato.
Se presenta aquí una serie de estos ejercicios
desarrollados.

3. Ejercicios de demostración
En ocasiones se nos pedirá demostrar que una
expresión trigonométrica compleja es igual a
otra, a veces totalmente distinta comparada
con la primera, como la que se ilustra en la
portada de esta presentación.
Aquí aprenderemos de forma práctica a
resolver algunos de estos ejercicios. Lo
haremos definiendo una estrategia a partir de
nuestros conocimientos de trigonometría y de
resolución de ecuaciones.

4. Estrategia
● Dada una expresión, primero nos fijamos en
cual es el miembro de ella más complejo.
Aquel que tenga más operaciones, ángulos
dobles, cocientes, etc.
● Nos fijamos en las expresiones
trigonométricas; si vemos la razón
trigonométrica de un ángulo doble, suma o
resta de ángulos, etc. hemos de
desarrollarlo hasta dejarlo como una
expresión que contenga, únicamente, senos
y cosenos de los ángulos dados.
Por ejemplo, si tenemos una expresión con un
sen(2a) buscamos su definición en función de
a. En este caso sen(2a)=2sen(a)cos(a).

5. ● Una vez desarrollada la expresión, lo que
hacemos es simplificarla. Para ello hemos de
sacar factor común, agrupar y reducir ... los
mismos pasos que realizábamos para
simplificar ecuaciones, teniendo en cuentaq ue
nuestras variables serán razones
trigonométricas, productos de ellas, sumas de
estas etc.
● A veces, podremos simplificar las
expresiones haciendo uso de las razones
fundamentales de la trigonometría (definición
de tangente de un ángulo y que la suma de los
cuadrados del seno y el coseno de un ángulo
es 1).

6. En los siguientes ejercicios pondremos a
prueba esta estrategia y la aplicaremos a
algunos casos concretos. Su nivel de dificultad
es variable, pero en todos ellos aparecerá una
serie de observaciones destinadas a la correcta
realización del ejercicio y la solución detallada
del mismo.
Se ha elegido mostrar las soluciones obtenidas
en cada ejercicio con una tipografía de
diferentes colores, indicando cada uno una
operación distinta a realizar.

7. 1. Demostrar la siguiente expresión
cos(a+b)+cos(a−b) 1
=
sen(a+b)+sen(a−b) tg (a)
Observaciones- Desarrollamos las razones
trigonométricas de la suma y la resta de los
ángulos a y b, y hemos de recordar la
definición de tangente de un ángulo.
Posteriormente simplificaremos

8. cos(a+b)+cos(a−b)
=
sen(a+b)+sen(a−b)
cos(a)cos(b)−sen(a) sen(b)+cos(a)cos(b)+sen(a) sen(b)
=
sen(a)cos(b)+sen(b)cos(a)+sen(a)cos(b)−sen(b)cos(a)
2cos(a)cos(b) cos(a) 1 1
= = =
2sen (a)cos(b) sen(a) sen(a) tg (a)
cos(a)

9. 2. Demostrar la siguiente expresión
2 sen(a)−sen(2 a) 1−cos(a)
=
2 sen(a)+sen(2 a) 1+cos(a)
Observaciones- Desarrollamos el miembro de
la izquierda de esta expresión, ya que el de la
derecha ya está en función de a. Hemos de
expresar las razones trigonométricas del
ángulo doble de a en función de coseno y seno
de a. Posteriormente sacamos factor común.

10. 2 sen(a)−sen(2 a) 2 sen(a)−2 sen(a)cos(a)
= =
2 sen(a)+sen(2 a) 2 sen(a)+2 sen(a)cos(a)
2 sen(a)(1−cos(a)) 1−cos(a)
=
2 sen(a)(1+cos(a)) 1+cos(a)

11. 3. Demostrar la siguiente expresión
2 x
2 tg ( x)cos ( )−sen( x) = tg ( x)
2
Observaciones- Desarrollamos el miembro de
la izquierda. Aquí hemos de tener en mente la
definición de coseno de un ángulo mitad.
Además, debemos recordar la propiedad
distributiva de la multiplicación.

12. 2 x
(
2 tg ( x)cos ( )−sen( x) = 2tg ( x)
2 2 )
1+cos( x)
−sen( x) =
tg ( x)+tg ( x)cos( x)−sen( x) =
sen( x)cos( x)
tg ( x)+ −sen( x) =
cos( x)
tg ( x)+sen( x)−sen( x) = tg ( x)

13. 4. Demostrar la siguiente expresión
cos( x− y) 1+tg ( x)tg ( y)
=
cos( x+ y) 1−tg ( x)tg ( y)
Observaciones- Desarrollamos el miembro de
la izquierda. Para ello, hacemos uso de la
definición de coseno de la resta de dos
ángulos. Posteriormente hemos de simplificar
las dos expresiones dividiendo por
cos(x)cos(y).

14. cos( x− y) cos( x)cos( y)+sen( x) sen( y)
= =
cos( x+ y) cos( x)cos( y)−sen( x) sen( y)
cos( x)cos( y) sen( x) sen( y) sen( x) sen( y)
+ 1+
cos( x)cos( y) cos( x)cos( y) cos( x) cos( y) 1−tg ( x)tg ( y)
= =
cos( x)cos( y) sen( x) sen( y) sen( x) sen( y) 1+tg ( x)tg ( y)
− 1−
cos( x)cos( y) cos( x)cos( y) cos( x) cos( y)

15. 5. Demostrar la siguiente expresión
cos( x)cos( x− y)+sen( x) sen( x− y) = cos( y)
Observaciones- Desarrollamos el miembro de
la izquierda. Recordamos la definición de seno
y coseno de la resta de dos ángulos. Sacamos
factor común. Cuidado con los signos.

16. cos( x) cos( x− y)+sen ( x) sen ( x− y) =
cos( x)(cos( x) cos( y)+sen ( x) sen( y))+sen ( x)(sen ( x) cos( y)−sen( y) cos( x)) =
cos 2 ( x)cos( y)+sen 2 ( x)cos( y)−cos( x) sen( x) sen( y)+sen( x) sen( y )cos( x) =
2 2
cos ( y) cos ( x)+cos( y) sen ( x) =
cos( y) ( cos2 ( x)+sen 2 ( x)) = cos( y)