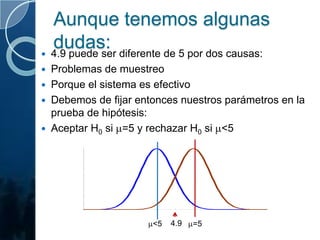
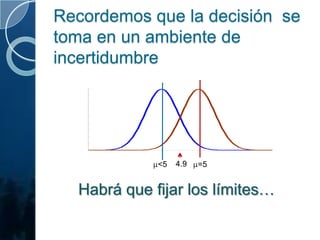
El documento presenta un análisis estadístico para probar si un sistema de cultivo de camarón puede producir 5 toneladas por hectárea. Se realizaron 36 pruebas que arrojaron un promedio de 4.9 toneladas. El autor formula una hipótesis nula de que el sistema puede lograr el objetivo frente a una alternativa de que no. Luego calcula límites críticos y probabilidades de errores tipo I y II para determinar si se acepta o rechaza la hipótesis nula.

1. Pruebas de Hipótesis: Segundo CapítuloDr. Carlos Cáceres Martínez, Curso de Estadística programa CIMACO, UABCS

2. ProblemaUn diseño de un sistema de cultivo intensivo de camarón tiene como meta producir 5 toneladas de rendimiento por hectárea (peso total). Se realizaron 36 pruebas y los resultados son los siguientes expresados en toneladas por hectárea:

3. Formulo la hipótesis¿Los resultados indican que se han alcanzado los objetivos o no?En este caso esta prueba es unilateral (una cola)Aunque podemos también decir que:Y tendremos una prueba bilateral (dos colas)

4. Aunque tenemos algunas dudas:4.9 puede ser diferente de 5 por dos causas:Problemas de muestreoPorque el sistema es efectivoDebemos de fijar entonces nuestros parámetros en la prueba de hipótesis:Aceptar H0 si =5 y rechazar H0 si <54.9<5=5

5. A cual de las dos distribuciones pertenece nuestro valor promedio (X=4.9):Esta decisión se toma sobre una realidad desconocida…Decisión

6. Recordemos que la decisión se toma en un ambiente de incertidumbreHabrá que fijar los límites…4.9<5=5

7. Para fijar los límites =5Región de rechazo de H0X0Es decir debemos de determinar cuando las diferencias con el valor de 5 ton/Ha dejaron de ser significativas..Región de aceptación de H0

8. Las diferencias dejan de ser significativas si:X0=-error (de muestreo)X0= -Z*XiX0= -ZXi/nAsumiendo que nuestro muestreo tiene una distribución normal entonces:X0= 5-(Z)0.48/36*Donde Z es el área bajo la curva normal en una distribución normal de datos muestreados.

9. La probabilidad del error tipo I será el nivel de significancia, así el Error I se controla sea al 5 o al 1% ejemplo:X0= 5-(2)0.48/36Mínimo relacionado con la curva normal, al recordar que ±2 representa el 95% de los valores probables en una distribución normal que pertenecen a De esta manera establecemos nuestra regla de decisión:

10. El valor resultante de la ecuación anterior es =4.84 en consecuencia si el valor de nuestro muestreo (4.9) es Xi entonces si Xi>X0=4.48 acepto Ho; y rechazo Ho en caso contrario.En otras palabrasEn conclusión estos resultados nos dicen que aceptemos Ho, el sistema de cultivo produce un valor perteneciente a un sistema de cultivo capaz de producir en promedio 5Ton/Ha (bajo la asunción de tener una distribución normal)Xi= 4.9 >X0=4.48Calculemos ahora la probabilidad de ocurrencia de los errores=P(error I)=P(rechazar Ho cuando Ho es verdadera).=P(X<4.48/=5)= p(Z<(4.84-5)/(0.48/36)P(Z<-2.0)Valor 0.977 positivo debemos restar la unidad 0.977-1=-0.0228Esta es la probabilidad de ocurrencia de 

11. Para el error =(P(error Tipo II) recordando aceptar Ho cuando es falsaPrimero debo de definir un punto económico, que estará fijado por el investigador. Este valor determina en términos reales cual es nuestro límite físico o material para nuestros experimentos. En este caso de manera arbitrario diremos que 4.75 Ton/Ha es el límite debajo de este valor la inversión en el desarrollo tecnológico deja de ser rentable.

12. =P(X<4.84/=4.75)=P(Z>4.84-4.75/(0.48/36))=(Z>1.125)= 0.864Valor económicoEste valor 0.864-1=0.136En otras palabras la probabilidad de ocurrencia de =13%

13. Para reducir  dejamos crecer , en este caso podemos probar con un valor en lugar de 2 podemos usar 2.28Pero si  =5% entonces para reducir  podemos aumentar el tamaño de la muestra.De esta manera tendremos en cuenta que reducir un error significará controlar el contrario. En los trabajos científicos se ha establecido un nivel de  =5% que significa controlar el error  en un nivel critico del 5%.

14. En nuestro ejemplo significa:45%5%=5X0=5-1.65(0.48/36)=4.87Área de la curva normal que comprende el 45% y deja libre el 5% (valor de tablas)X0

15. Valores de Z para una sola cola

16. X0=5-1.65(0.48/36)=4.87Por lo tanto 4.78 es el límite en consecuencia 4.9 está en la región de aceptación de H0, re-calculamos la probabilidad de ocurrencia de =P(Error II)=P(X>4.87/=4.75)=P(Z>(4.87-4.75)/(0.48/36)= 1.5Lo busco en la tabla anterior y encuentro Z=0.4332, este valor se lo resto a la mitad de la curva:0.5- 0.4332= 0.067, es decir el 6.7% de probabilidad

17. Resumiendo las alternativas de cálculo tendremos