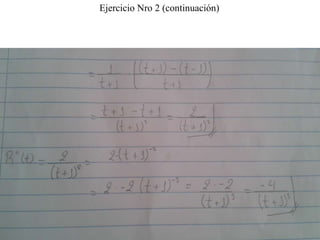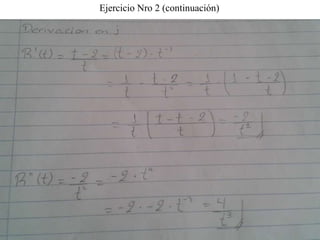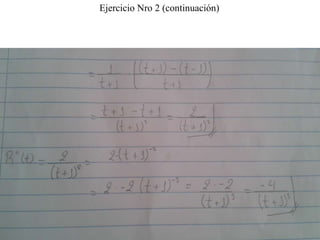
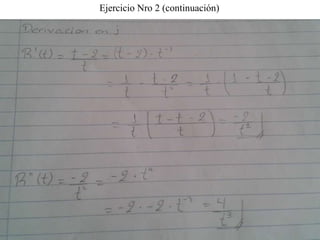
Este documento presenta las preguntas de un examen individual de matemáticas compuesto por 5 ejercicios. Los ejercicios incluyen: 1) representar gráficamente un campo vectorial, 2) calcular una derivada parcial, 3) calcular el rotacional y divergencia de un campo vectorial, 4) obtener la ecuación de un plano tangente, y 5) obtener ecuaciones simétricas de una recta normal.

1. UNIVERSIDAD FERMIN TORO
CABUDARE.ESTADO LARA
Apellido Di Benedetto Nombres Cesidio Antonio
Cédula 24166027 Fecha 8-12-2015
Examen Individual
On line
1. Muestre en una figura los vectores representativos del campo vectorial
jxxyiyxF 2
4
1
2
1
),( += ( 2ptos)
2. Calcule )()( tRytR ¢¢¢ si
si j
t
t
i
t
t
tR
2
1
1
)(
-
+
+
-
= ( 2ptos)
3. Calcule el rot F y div R para el campo vectorial F dado
kzjyxiyxzyxF 22222
11),,( ++++++= ( 2ptos)
4. Obtenga una ecuación del plano tangente a la superficie en el punto
dado: ln5)(3,4,puntoelenln),( 22
yxyxh += ( 2 ptos)
5. Obtenga ecuaciones simétricas de la recta normal a la superficie en el
punto indicado.
÷
ø
ö
ç
è
æ
=
4
1,1,puntoelenarctan
p
x
y
z ( 2ptos)
10

2. Ejercicio Nro 2

3. Ejercicio Nro 2 (continuación)

4. Ejercicio Nro 2 (continuación)

5. Ejercicio Nro 2 (continuación)

6. Ejercicio Nro 3

7. Ejercicio Nro 4

8. Ejercicio Nro 5