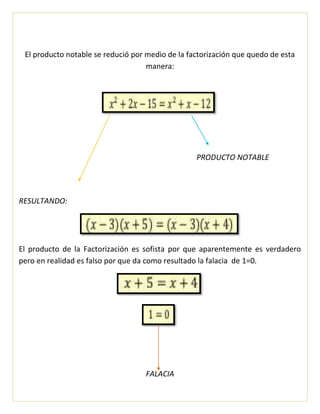
El documento presenta un procedimiento matemático falaz y sofista que conduce a la conclusión 1=0. Se explican conceptos matemáticos como lógica aristotélica, geometría euclidiana, demostración matemática, argumento, falaz, sofista, deductivo, inductivo y operaciones algebraicas. Luego, se muestra el procedimiento falaz paso a paso y finalmente el procedimiento correcto que conduce a la conclusión verdadera 0=0.

1. Integrantes:
Sofía Yadira Cortinas Padilla
Irma Laura Garcia Favela
Luis Humberto Guitierréz Garrido
1-A
Matematicas 1
´´el ignorante afirma, el sabio duda y reflexiona.´´
(Aristotéles)
16 de septiembre del 2013

2. LAS MATEMÁTICAS SOFISTAS
1era
Etapa
Para resolver el problema matemático, que se muestra a continuación es
fundamental saber el significado de cada uno de los términos que se necesitan
para su resolución.
Lógica aristotélica: Se basa en encontrar la lógica en los planteamientos que hacemos.
Geometría euclidiana: Es la geometría que usamos cotidianamente como: ángulos, segmentos,
rectas, etc.
Demostración: Es la prueba de que algo es verdadero
Demostración matemática: Es un argumento lógico para afirmar un planteamiento por medio de
diferentes métodos.
Argumento: Es el razonamiento que usamos para poder comprobar que estamos en lo correcto.
Falaz: Es un argumento o procedimiento no valido.
Sofista: Era los antiguos filósofos que se basaban en el en el razonamiento para explicar algún
fenómeno. A su vez optaban pensamientos que eran errores con apariencia de verdades.
Deductivo: Razonamiento que parte de lo general a lo particular.
Inductivo: Razonamiento que parte de lo particular a lo general.
Afirmación: Asegurar o dar por cierta una cosa.
Operaciones algebraicas básicas: Son expresiones con letras, números y signos de operación
representan variables incógnitas.
Productos notables: Es el nombre que reciben multiplicaciones con expresiones algebraicas.
Factorización: Es una técnica que consiste en la descomposición de una expresión matemática.
Propiedades de igualdad: Comparación de valores representados por el signo igual, la demostración
se relaciona con propiedades de la igualdad ya que todas cuentan con su signo.

3. A continuación se muestran la siguiente secuencia de pasos alegebraicos desde
luego falaz y sofista:
X=3
2x=x+3
X²+2x=x²+x+3
X²+2x-15=x²+x-12
(x-3)(X+5)=(x-3) (x+4)
X+5=x+4
1=0
Nos da un ejemplo de lógica aristotélica, porque x puede tener cualquier valor, de
igual manera podemos aplicar la geometría ecuclidiana teniendo el valor de x, se
podrá formar una recta.
Tratamos de demostrar que es un razonamiento falso e incorrecto por medio de
una demostración matemática utilizando operaciones algebraicas básicas; como lo
son la suma, resta y los signos de operación.
Se aplicaron las propiedades de la igualdad en los siguentes pasos:

4. El producto notable se redució por medio de la factorización que quedo de esta
manera:
PRODUCTO NOTABLE
RESULTANDO:
El producto de la Factorización es sofista por que aparentemente es verdadero
pero en realidad es falso por que da como resultado la falacia de 1=0.
FALACIA

5. PROCEDIMIENTO CORRECTO
Se sustituyó la x por su valor real: la operación quedo de la siguiente
forma:
X=3
Valor de X
La operación quedo de la siguiente forma:
2(3)= (3)+3
(3)²+2(3)= (3) ²+ (3) +3
(3)²+2(3)-15= (3) ²+ (3)-12
((3)-3)((3)+5)= ((3)-3) ((3)+4)
(3)+5= (3)+4
6=6
9+6= 9+6
9+6-15=9+3-12
(0)(8)= (0) (7)
Resultado Final
1
2
0=0