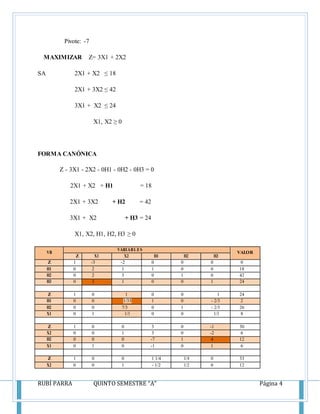
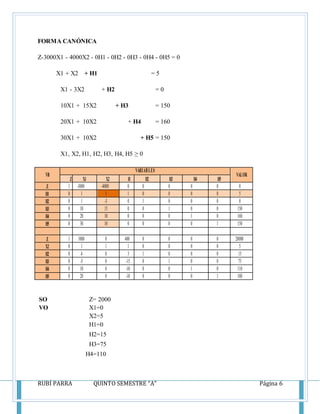
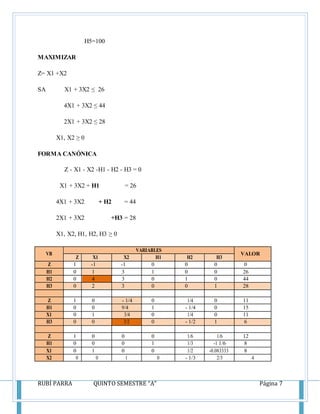
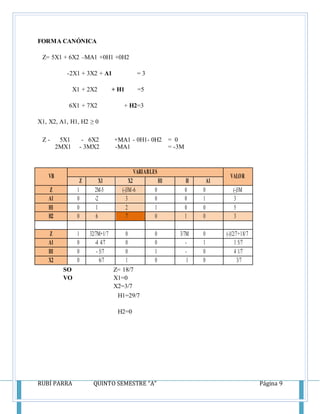
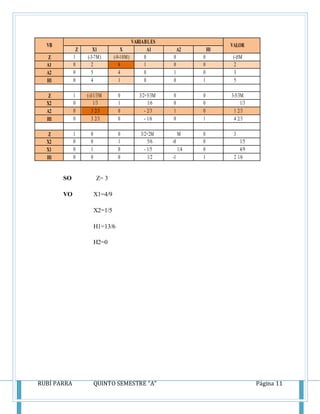
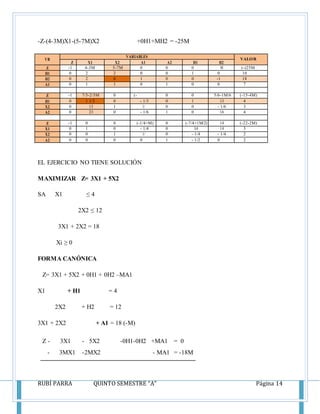
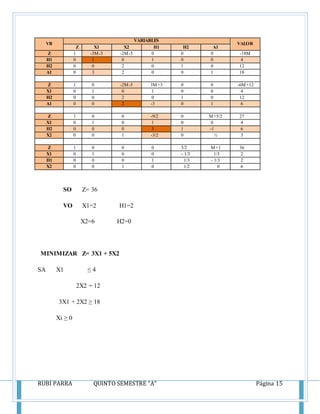
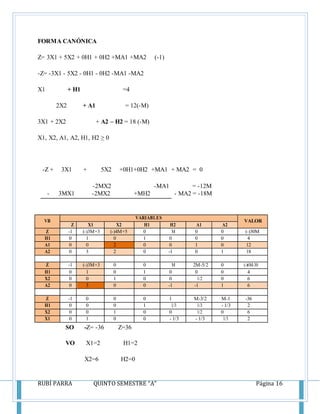
Este documento presenta los conceptos y métodos del método simplex para resolver problemas de programación lineal, incluyendo las reglas de Crammer, el método de Gauss-Jordan, y la técnica de la holgura. También incluye ejemplos resueltos de problemas de maximización usando el método simplex.

1. RUBÍ PARRA QUINTO SEMESTRE “A” Página 1
MÉTODO SIMPLEX
Regla de Crammer (3x3) (2x2); Método de Gauss y Jordan
1.
2 3 4 3
4 5 2 2
7 9 4 4
2.
3.
7 2 4 6 5 3 13/4 -5/2 -3/8 0 2 3/2
4 3 3 5 2 3 7/8 -3/4 -11/8 0 -1/2 7/4
5 6 7 8 4 2 5/8 ¾ 7/8 1 ½ ¼
8 9 7 6 3 3 17/4 9/2 7/4 0 0 3/2
4 3 5 2 7 4 11/4 3/2 13/4 0 6 7/2
4.
5.
-2/5 0 14/5 9/5
4/5 1 2/5 2/5
-1/5 0 2/5 2/5
5 2 2 2 3 25/7 0 10/7 -4/7 17
/72 3 3 4 2 -1/7 0 15/7 1/7 8/
74 3 2 2 5 13/7 0 8/7 -
13/
7
29
/7
5 7 2 9 2 5/7 1 2/7 9/7 2/
7
-15/2 -4 0 -1/2 -11/2
-13/3 -7/3 0 -11/3 -11/3
7/6 2/3 1 5/6 5/6
-11/6 -1/3 0 11/6 17/6
3 2 9 7 2
5 3 8 3 3
7 4 6 5 5
4 3 5 6 7

2. RUBÍ PARRA QUINTO SEMESTRE “A” Página 2
Z A B H1 H2 VALO R
Z -20 -30 0 0 0
H1 2 2 1 0 5
H2 1 1 0 1 3
CONCEPTOS A CONSIDERAR
PIVOTE.- el Pivote es el número que se interseca entre el vector entrante y el vector saliente.
VECTOR ENTRANTE.- es la columna que contiene el número más pequeño.
VECTOR SALIENTE.- número positivo más pequeño que resulta de la división de los
términos independientes para el vector entrante.
se aplica a problemas de maximización porque los de minimización requieren otro
tratamiento.
EJEMPLO
MAXIMIZAR
Z = 20A + 30B
SUJETO A
2A +2B ≤ 5
A + B ≤ 3
Vector entrante: B
Vector Saliente: H1
Pivote: 2
3 4 2 5 3 2
4 2 3 6 2 3
2 8 4 7 9 4
3 5 9 8 3 2
8 3 2 5 3 2
-5 1 0 0 0 0
-8 -5/2 0 -3/2 -5/2 0
-14 2 0 -3 3 0
-33 -17/2 0 -29/2 -21/2 -7
4 3/2 1 5/2 3/2 1

3. RUBÍ PARRA QUINTO SEMESTRE “A” Página 3
2. MAX Z= 3X1 + 4X2 + 9X3
Sa 2X1 + 2X2 ≤ 10
2X2 + 5 X3 ≤ 16
3X1 – 2X2 -7X3 ≤ 9
X1, X2, X3 ≥ 0
 SE TRANSFORMA A UNA IGUALDAD
Z - 3X1 - 4X2 - 9X3 = 0
2X1+2X2 = 10
2X2 + 5X3 = 16
3X1 – 2X2 -7X3 = 9
Xj ≥ 0 j=1…3
HOLGURAS
Z - 3X1 - 4X2 - 9X3 = 0
2X1+2X2 +H1 = 10
2X2 + 5X3 +H2 = 16
3X1 – 2X2 -7X3 + H3 = 9
VB EC Z X1
X2
X
3
H1 H2 H3
VALORZ 0 1 -3 -4 -9 0 0 0 0
H1 1 0 2 2 0 1 0 0 10
H2 2 0 0 2 5 0 1 0 16
H3 3 0 3 2 -7 0 0 1 9
Vector entrante: X3
Vector Saliente: H3

4. RUBÍ PARRA QUINTO SEMESTRE “A” Página 4
Pivote: -7
MAXIMIZAR Z= 3X1 + 2X2
SA 2X1 + X2 ≤ 18
2X1 + 3X2 ≤ 42
3X1 + X2 ≤ 24
X1, X2 ≥ 0
FORMA CANÓNICA
Z - 3X1 - 2X2 - 0H1 - 0H2 - 0H3 = 0
2X1 + X2 + H1 = 18
2X1 + 3X2 + H2 = 42
3X1 + X2 + H3 = 24
X1, X2, H1, H2, H3 ≥ 0
VB
VARIABLES
VALOR
Z X1 X2 H1 H2 H3
Z 1 -3 -2 0 0 0 0
H1 0 2 1 1 0 0 18
H2 0 2 3 0 1 0 42
H3 0 3 1 0 0 1 24
Z 1 0 1 0 0 1 24
H1 0 0 1/33
/3
1 0 - 2/3 2
H2 0 0 7/3 0 1 - 2/3 26
X1 0 1 1/3 0 0 1/3 8
Z 1 0 0 3 0 -1 30
X2 0 0 1 3 0 -2 6
H2 0 0 0 -7 1 4 12
X1 0 1 0 -1 0 1 6
Z 1 0 0 1 1/4 1/4 0 33
X2 0 0 1 - 1/2 1/2 0 12

5. RUBÍ PARRA QUINTO SEMESTRE “A” Página 5
H3 0 0 0 -1 3/4 1/4 1 3
X1 0 1 0 3/4 - 1/4 0 3
SO Z= 33
VO X1=3
X2=12
H1= 0
H2=0
H3=3
MAXIMIZAR Z= 3000X1 + 4000X2
SA X1 + X2 ≤ 5
X1 - 3X2 ≤ 0
10X1 + 15X2 ≤ 150
20X1 + 10X2 ≤ 160
30X1 + 10X2 ≤ 150
X1, X2 ≥0

6. RUBÍ PARRA QUINTO SEMESTRE “A” Página 6
FORMA CANÓNICA
Z-3000X1 - 4000X2 - 0H1 - 0H2 - 0H3 - 0H4 - 0H5 = 0
X1 + X2 + H1 = 5
X1 - 3X2 + H2 = 0
10X1 + 15X2 + H3 = 150
20X1 + 10X2 + H4 = 160
30X1 + 10X2 + H5 = 150
X1, X2, H1, H2, H3, H4, H5 ≥ 0
SO Z= 2000
VO X1=0
X2=5
H1=0
H2=15
H3=75
H4=110
VB
VARIABLES
VALOR
Z X1 X2 H
1
H2 H3 H4 H5
Z 1 -3000 -4000 0 0 0 0 0 0
H1 0 1 1 1 0 0 0 0 5
H2 0 1 -3 0 1 0 0 0 0
H3 0 10 15 0 0 1 0 0 150
H4 0 20 10 0 0 0 1 0 160
H5 0 30 10 0 0 0 0 1 150
Z 1 1000 0 400
0
0 0 0 0 20000
X2 0 1 1 1 0 0 0 0 5
H2 0 4 0 3 1 0 0 0 15
H3 0 -5 0 -15 0 1 0 0 75
H4 0 10 0 -10 0 0 1 0 110
H5 0 20 0 -10 0 0 0 1 100

7. RUBÍ PARRA QUINTO SEMESTRE “A” Página 7
H5=100
MAXIMIZAR
Z= X1 +X2
SA X1 + 3X2 ≤ 26
4X1 + 3X2 ≤ 44
2X1 + 3X2 ≤ 28
X1, X2 ≥ 0
FORMA CANÓNICA
Z - X1 - X2 -H1 - H2 - H3 = 0
X1 + 3X2 + H1 = 26
4X1 + 3X2 + H2 = 44
2X1 + 3X2 +H3 = 28
X1, X2, H1, H2, H3 ≥ 0
VB
VARIABLES
VALOR
Z X1 X2 H1 H2 H3
Z 1 -1 -1 0 0 0 0
H1 0 1 3 1 0 0 26
H2 0 4 3 0 1 0 44
H3 0 2 3 0 0 1 28
Z 1 0 - 1/4 0 1/4 0 11
H1 0 0 9/4 1 - 1/4 0 15
X1 0 1 3/4 0 1/4 0 11
H3 0 0 3/2 0 - 1/2 1 6
Z 1 0 0 0 1/6 1/6 12
H1 0 0 0 1 1/3 -1 1/6 8
X1 0 1 0 0 1/2 -0.083333 8
X2 0 0 1 0 - 1/3 2/3 4

8. RUBÍ PARRA QUINTO SEMESTRE “A” Página 8
SO Z=12
VO X1=8 H1=8
X2=4 H2=0
H3=0
TÉCNICA DE LA M
AÑADIR:
≤ +H1
= +A1
≥ -H1+A1
Max –M
Min +M
EJEMPLOS:
MAXIMIZAR Z= 5X1 + 6X2
SA -2X1 + 3X2 = 3
X1 + 2X2 ≤ 5
6X1 + 7X2 ≤ 3
X1, X2 ≥ 0

9. RUBÍ PARRA QUINTO SEMESTRE “A” Página 9
FORMA CANÓNICA
Z= 5X1 + 6X2 –MA1 +0H1 +0H2
-2X1 + 3X2 + A1 = 3
X1 + 2X2 + H1 =5
6X1 + 7X2 + H2=3
X1, X2, A1, H1, H2 ≥ 0
Z - 5X1 - 6X2 +MA1 - 0H1- 0H2 = 0
2MX1 - 3MX2 -MA1 = -3M
VB
VARIABLES
VALOR
Z X1 X2 H1 H
2
A1
Z 1 2M-5 (-)3M-6 0 0 0 (-)3M
A1 0 -2 3 0 0 1 3
H1 0 1 2 1 0 0 5
H2 0 6 7 0 1 0 3
Z 1 32/7M+1/7 0 0 3/7M
+6/7
0 (-)12/7+18/7
A1 0 -4 4/7 0 0 -
3/
7
1 1 5/7
H1 0 - 5/7 0 1 -
2/
7
0 4 1/7
X2 0 6/7 1 0 1
/
7
0 3/7
SO Z= 18/7
VO X1=0
X2=3/7
H1=29/7
H2=0

10. RUBÍ PARRA QUINTO SEMESTRE “A” Página 10
MAXIMIZAR Z= 3X1 + 9X2
SA 2X1 + 6X2 = 2
5X1 + 4X2 = 3
4X1 + X2 ≤ 5
X1, X2 ≥ 0
FORMA CANÓNICA
Z= 3X1 + 9X2 –MA1 –MA2 +0H1
2X1 + 6X2 +A1 = 2 (-M)
5X1 + 4X2 +A2 = 3 (-M)
4X1 + X2 +H1=5
X1, X2, A1, A2, H1 ≥0
Z - 3X1 - 9X2 +MA1 +MA2 - 0H1= 0
-2MX1 - 6MX2 -MA1 = -2M
-5MX1 – 4MX2 -MA2 = -3M Z+

11. RUBÍ PARRA QUINTO SEMESTRE “A” Página 11
VB
VARIABLES
VALOR
Z X1 X
2
A1 A2 H1
Z 1 (-3-7M) (-9-10M) 0 0 0 (-)5M
A1 0 2 6 1 0 0 2
A2 0 5 4 0 1 0 3
H1 0 4 1 0 0 1 5
Z 1 (-)11/3M 0 3/2+5/3M 0 0 3-5/3M
X2 0 1/3 1 1/6 0 0 1/3
A2 0 3 2/3 0 - 2/3 1 0 1 2/3
H1 0 3 2/3 0 - 1/6 0 1 4 2/3
Z 1 0 0 3/2+2M M 0 3
X2 0 0 1 5/6 -0 0 1/5
X1 0 1 0 - 1/5 1/4 0 4/9
H1 0 0 0 1/2 -1 1 2 1/6
SO Z= 3
VO X1=4/9
X2=1/5
H1=13/6
H2=0

12. RUBÍ PARRA QUINTO SEMESTRE “A” Página 12
MINIMIZACIÓN
SE MULTIPLICA A LA FUNCIÓN OBJETIVO POR -1 Y SE RESULEVE COMO UN
PROBLEMA DE MAXIMIZACIÓN.
MINIMIZAR Z= 3/2X1+2X2
SA 2X1 + 2X2 ≤ 8
2X1 + 6X2 ≥ 12
X1, X2 ≥ 0
FORMA CANÓNICA
Z= 3/2X1+ 2X2 + MA1 +0H1+ 0H2
2X1 + 2X2 + H1 = 8
2X1 + 6X2 +A1-H2 =12 (M)
X1, X2, A1, H1, H2 ≥ 0
Z – 3/2X1 -2X2
2MX1 + 6MX2
- MA1 -0H1- 0H2 = 0
+MA1 -MH2 = 12M
Z+(2M-3/2)X1+(6M-2)X2
-Z-(3/2-2M)X1-(2-6M)X2
-0H1–MH2= 12M
+0H1+MH2= -12M
(-1)
VB
VARIABLES
VALOR
Z X1 X
2
A1 H1 H2
Z -1 3/2-2M 2-6M 0 0 M (-)12M
H1 0 2 2 0 1 0 8
A1 0 2 6 1 0 -1 12
Z -1 5/6 0 (-1/3+M) 0 1/3 -4
H1 0 1 1/3 0 - 1/3 1 1/3 4
X2 0 1/3 1 1/6 0 - 1/6 2

13. RUBÍ PARRA QUINTO SEMESTRE “A” Página 13
SO -Z= -4 Z=4
VO X1=0
X2=2
H1=4
H2=0
MINIMIZAR Z= 4X1 + 5X2
SA 2X1 + 2X2 ≤ 10
2X1 + 6X2 ≥ 18
X1 + X2 = 7
Xi ≥ 0
FORMA CANÓNICA
Z= 4X1 + 5X2 + MA1 + MA2 + 0H1 + 0H2
2X1 + 2X2 + H1 = 10
2X1 + 6X2 +A1 – H2 =18 (M)
X1 + X2 +A2 = 7 (M) X1,
X2, A1, A2, H1, H2 ≥ 0
Z - 4X1 - 5X2 - MA1 - MA2 - 0H1 - 0H2 = 0
2MX1 + 6MX2 +MA1 – MH2 = 18M
MX1 + MX2 +MA2 = 7M
Z+(3M-4)X1+(7M-5)X2 -0H1-MH2 = 25M (-1)

14. RUBÍ PARRA QUINTO SEMESTRE “A” Página 14
-Z-(4-3M)X1-(5-7M)X2 +0H1+MH2 = -25M
VB
VARIABLES
VALOR
Z X1 X2 A1 A2 H1 H2
Z -1 4-3M 5-7M 0 0 0 M (-)25M
H1 0 2 2 0 0 1 0 10
H2 0 2 6 1 0 0 -1 18
A1 0 1 1 0 1 0 0 7
Z -1 7/3-2/3M 0 (-
5/6+7M/6)
0 0 5/6-1M/6 (-15-4M)
H1 0 1 1/3 0 - 1/3 0 1 1/3 4
X2 0 1/3 1 1/
6
0 0 - 1/6 3
A2 0 2/3 0 - 1/6 1 0 1/6 4
Z -1 0 0 (-1/4+M) 0 (-7/4+1M/2) 1/4 (-22-2M)
X1 0 1 0 - 1/4 0 3/4 1/4 3
X2 0 0 1 1/
4
0 - 1/4 - 1/4 2
A2 0 0 0 0 1 - 1/2 0 2
EL EJERCICIO NO TIENE SOLUCIÓN
MAXIMIZAR Z= 3X1 + 5X2
SA X1 ≤ 4
2X2 ≤ 12
3X1 + 2X2 = 18
Xi ≥ 0
FORMA CANÓNICA
Z= 3X1 + 5X2 + 0H1 + 0H2 –MA1
X1 + H1 = 4
2X2 + H2 = 12
3X1 + 2X2 + A1 = 18 (-M)
Z - 3X1 - 5X2 -0H1-0H2 +MA1 = 0
- 3MX1 -2MX2 - MA1 = -18M

15. RUBÍ PARRA QUINTO SEMESTRE “A” Página 15
VB
VARIABLES
VALOR
Z X1 X2 H1 H2 A1
Z 1 -3M-3 -2M-5 0 0 0 -18M
H1 0 1 0 1 0 0 4
H2 0 0 2 0 1 0 12
A1 0 3 2 0 0 1 18
Z 1 0 -2M-5 3M+3 0 0 -6M+12
X1 0 1 0 1 0 0 4
H2 0 0 2 0 1 0 12
A1 0 0 2 -3 0 1 6
Z 1 0 0 -9/2 0 M+5/2 27
X1 0 1 0 1 0 0 4
H2 0 0 0 3 1 -1 6
X2 0 0 1 -3/2 0 ½ 3
Z 1 0 0 0 3/2 M+1 36
X1 0 1 0 0 - 1/3 1/3 2
H1 0 0 0 1 1/3 - 1/3 2
X2 0 0 1 0 1/2 0 6
SO Z= 36
VO X1=2 H1=2
X2=6 H2=0
MINIMIZAR Z= 3X1 + 5X2
SA X1 ≤ 4
2X2 = 12
3X1 + 2X2 ≥ 18
Xi ≥ 0

16. RUBÍ PARRA QUINTO SEMESTRE “A” Página 16
FORMA CANÓNICA
Z= 3X1 + 5X2 + 0H1 + 0H2 +MA1 +MA2 (-1)
-Z= -3X1 - 5X2 - 0H1 - 0H2 -MA1 -MA2
X1 + H1 =4
2X2 + A1 = 12(-M)
3X1 + 2X2 + A2 – H2 = 18 (-M)
X1, X2, A1, A2, H1, H2 ≥ 0
-Z + 3X1 + 5X2 +0H1+0H2 +MA1 + MA2 = 0
-2MX2 -MA1 = -12M
- 3MX1 -2MX2 +MH2 - MA2 = -18M
VB
VARIABLES
VALOR
Z X1 X2 H1 H2 A1 A2
Z -1 (-)3M+3 (-)4M+5 0 M 0 0 (-)30M
H1 0 1 0 1 0 0 0 4
A1 0 0 2 0 0 1 0 12
A2 0 3 2 0 -1 0 1 18
Z -1 (-)3M+3 0 0 M 2M-5/2 0 (-)6M-30
H1 0 1 0 1 0 0 0 4
X2 0 0 1 0 0 1/2 0 6
A2 0 3 0 0 -1 -1 1 6
Z -1 0 0 0 1 M-3/2 M-1 -36
H1 0 0 0 1 1/3 1/3 - 1/3 2
X2 0 0 1 0 0 1/2 0 6
X1 0 1 0 0 - 1/3 - 1/3 1/3 2
SO -Z= -36 Z=36
VO X1=2 H1=2
X2=6 H2=0