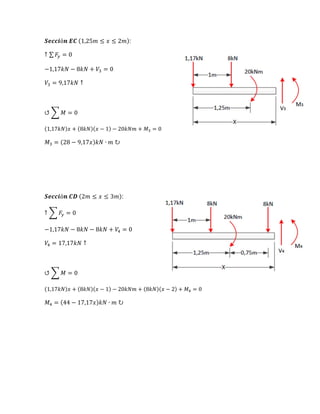
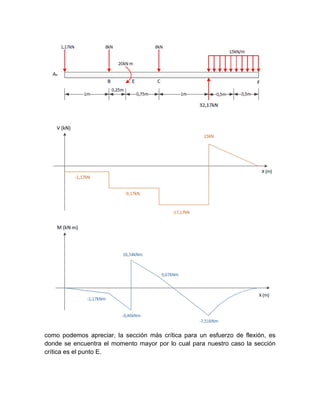
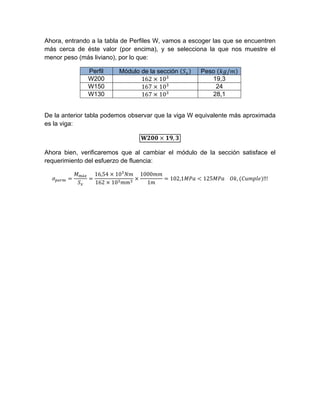
El documento presenta la solución a un problema de ingeniería estructural que involucra: 1) calcular el centroide y momento de inercia de una sección transversal compuesta, 2) determinar las reacciones en una viga, 3) derivar ecuaciones para diagramas de corte y momento, 4) calcular esfuerzos máximos de flexión, 5) seleccionar un perfil estructural que satisfaga los requerimientos de esfuerzo.

1. Problema 3
Solución:
a. Calculemos el centroide de la sección
transversal de la siguiente manera:
Elemento ’ ’
1 126 7776 979776
2 54 7776 419904
Total 15552 1399680
Ahora, el centroide se calcula asi:
∑ ′
∑
1339680
15552
Ahora hallemos el momento de inercia de la figura compuesta, se la siguiente
manera:
1

2. Donde:
̅ ′
1
12
′
1
12
216 36 7776 90 126
10917504
̅ ′
1
12
′
1
12
72 108 7776 90 54
17635968
Por lo tanto el momento de Inercia de la figura compuesta será:
10917504 17635968
b. Ahora calcularemos las reacciones de la viga mostrada en el DCL usando las
ecuaciones de equilibrio:
 Reacciones:
↺ 0
1 8 20 ∙ 2 8 3 3,5 15 0
32,17 ↑

3. ↑ 0
8 8 32,17 15 0 → 1,17 ↓
→ 0
0
Ahora para poder realizar los diagramas de fuerzas cortantes y de momentos
flectores, debemos hallar las ecuaciones que rigen a estas curvas haciendo cortes
en la viga como se muestra a continuación:
ó 0 1 :
↑ 0
1,17 0 → 1,17 ↑
↺ 0
1,17 0 → 1,17 ∙ ↻
ó 1 1,25 :
↑ ∑ 0
1,17 8 0 → 9,17 ↑
↺ 0
1,17 8 1 0
8 9,17 ∙ ↻

4. ó 1,25 2 :
↑ ∑ 0
1,17 8 0
9,17 ↑
↺ 0
1,17 8 1 20 0
28 9,17 ∙ ↻
ó 2 3 :
↑ 0
1,17 8 8 0
17,17 ↑
↺ 0
1,17 8 1 20 8 2 0
44 17,17 ∙ ↻

5. ó 3 4 :
↑ 0
1,17 8 8 32,17 15 3 0
15 60 ↑
↺ 0
1,17 8 1 20 8 2 32,17 3
15
2
3 0
60 120 7,5 ∙ ↻
Ya que tenemos las ecuaciones que gobiernan las gráficas tenemos que los
diagramas serán de la siguiente manera

6. como podemos apreciar, la sección más crítica para un esfuerzo de flexión, es
donde se encuentra el momento mayor por lo cual para nuestro caso la sección
crítica es el punto E.

7. c. Los esfuerzos máximos de flexión (para tensión y compresión) se hallan de la
siguiente manera:
á
Para el esfuerzo de flexión por tensión, tenemos que:
á 16,54 10 90
28553472
1000
1
,
Para el esfuerzo de flexión por Compresión, tenemos que:
á 16,54 10 144 90
28553472
1000
1
,
El radio de curvatura se calcula de la siguiente manera. 210
1
→
á
210 10 ⁄ 28553472
16,54 10
1000
1
362528,9674 ,
d. Calculemos el esfuerzo permisible para poder hallar el módulo de la sección,
de la siguiente manera:
250
2
125
Ahora bien, el módulo de la sección lo vamos a calcular bajo las siguientes
relaciones:
á á
→
á 16,54 10
125
1000
1
1
1
132,32 10

8. Ahora, entrando a la tabla de Perfiles W, vamos a escoger las que se encuentren
más cerca de éste valor (por encima), y se selecciona la que nos muestre el
menor peso (más liviano), por lo que:
Perfil Módulo de la sección Peso /
W200 162 10 19,3
W150 167 10 24
W130 167 10 28,1
De la anterior tabla podemos observar que la viga W equivalente más aproximada
es la viga:
,
Ahora bien, verificaremos que al cambiar el módulo de la sección satisface el
requerimiento del esfuerzo de fluencia:
á 16,54 10
162 10
1000
1
102,1 125 , ‼!