Este documento presenta el estudio de cuatro funciones, identificando en cada caso: el dominio, los puntos de corte, las asíntotas, y los máximos, mínimos y puntos de inflexión. Se analizan las propiedades de cada función a través de cálculos y derivadas para poder representar gráficamente cada una.
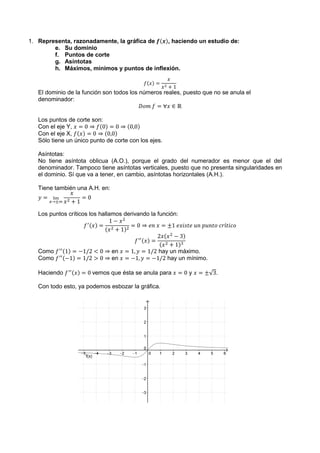
![2. Representa, razonadamente, la gráfica de 𝒇𝒇(𝒙𝒙), haciendo un estudio de:
a. Su dominio
b. Puntos de corte
c. Asíntotas
d. Máximos, mínimos y puntos de inflexión.
𝑓𝑓(𝑥𝑥) =
𝑥𝑥2
− 2
𝑥𝑥
Lo primero de todo, vamos a operar para conseguir una función más fácil de manejar.
𝑓𝑓(𝑥𝑥) = 𝑥𝑥 −
2
𝑥𝑥
Lo que nos será útil más adelante cuando tengamos que derivar. El dominio de la función
viene limitado por los puntos donde se anula el denominador, es decir:
𝐷𝐷𝐷𝐷𝐷𝐷 𝑓𝑓 = ℝ − {0}
Puesto que tiene una indeterminación en 𝑥𝑥 = 0, sólo presenta puntos de corte con el eje X
(𝑓𝑓(𝑥𝑥) = 0), donde
𝑥𝑥2
− 2 = 0 ⇒ 𝑥𝑥 = ±√2
Es decir, tiene dos puntos de corte con el eje X, en �−√2, 0� y en �√2, 0�
No tiene asíntota horizontal (A.H.), porque el grado del numerador es una unidad mayor que
el del denominador. Sí que va a tener, en cambio, asíntotas verticales (A.V.) y oblicuas
(A.O.).
Tiene una A.V. en 𝑥𝑥 = 0 y se da que:
lim
𝑥𝑥→0+
𝑥𝑥2
− 2
𝑥𝑥
= lim
𝑥𝑥→0+
𝑥𝑥 −
2
𝑥𝑥
= −∞ lim
𝑥𝑥→0−
𝑥𝑥2
− 2
𝑥𝑥
= lim
𝑥𝑥→0−
𝑥𝑥 −
2
𝑥𝑥
= +∞
La pendiente de la asíntota oblicua la hallo mediante
𝑚𝑚 = lim
𝑥𝑥→+∞
𝑓𝑓(𝑥𝑥)
𝑥𝑥
= lim
𝑥𝑥→+∞
𝑥𝑥2
− 2
𝑥𝑥2
= 1
La ordenada en el origen se obtiene, a su vez, mediante
𝑛𝑛 = lim
𝑥𝑥→+∞
[𝑓𝑓(𝑥𝑥) − 𝑚𝑚𝑚𝑚] = lim
𝑥𝑥→+∞
�
𝑥𝑥2
− 2
𝑥𝑥
− 𝑥𝑥� = lim
𝑥𝑥→+∞
�
𝑥𝑥2
− 2 − 𝑥𝑥2
𝑥𝑥
� = lim
𝑥𝑥→+∞
−2
𝑥𝑥
= 0
Por lo tanto, 𝑓𝑓(𝑥𝑥) tendrá una asíntota oblicua en 𝑦𝑦 = 𝑥𝑥.
Los puntos críticos los hallamos derivando la función:
𝑓𝑓′(𝑥𝑥) =
𝑑𝑑
𝑑𝑑𝑑𝑑
�𝑥𝑥 −
2
𝑥𝑥
� = 1 +
2
𝑥𝑥2
= 0 ⇒ 𝑥𝑥2
= −2 ≠ 0 ∀𝑥𝑥 ∈ ℝ ⇒ ∄𝑚𝑚á𝑥𝑥𝑥𝑥𝑥𝑥𝑥𝑥𝑥𝑥 𝑜𝑜 𝑚𝑚í𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛.
La derivada segunda de 𝑓𝑓(𝑥𝑥), 𝑓𝑓′′(𝑥𝑥), nos dará los posibles puntos de inflexión:
𝑓𝑓′′(𝑥𝑥) = −
4
𝑥𝑥3
≠ 0 ∀𝑥𝑥 ∈ ℝ
Por lo que tampoco tiene puntos de inflexión.
Ya con todo esto podemos hacernos una idea de cómo es la función y representarla.](https://image.slidesharecdn.com/grficasdeexmenes1415-150605153201-lva1-app6892/85/Ejercicios-de-representacion-Grafica-de-funciones-2-320.jpg)



