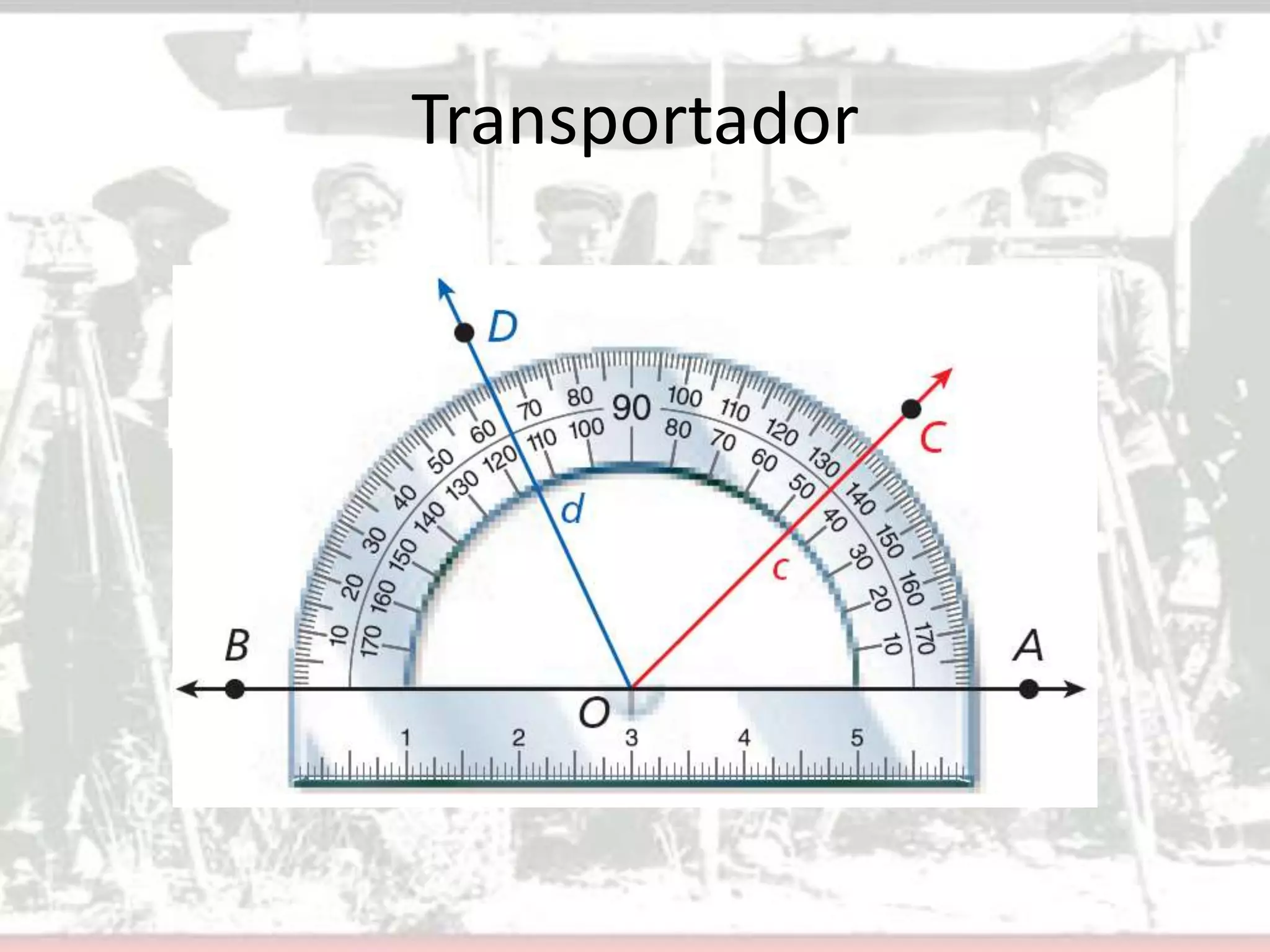
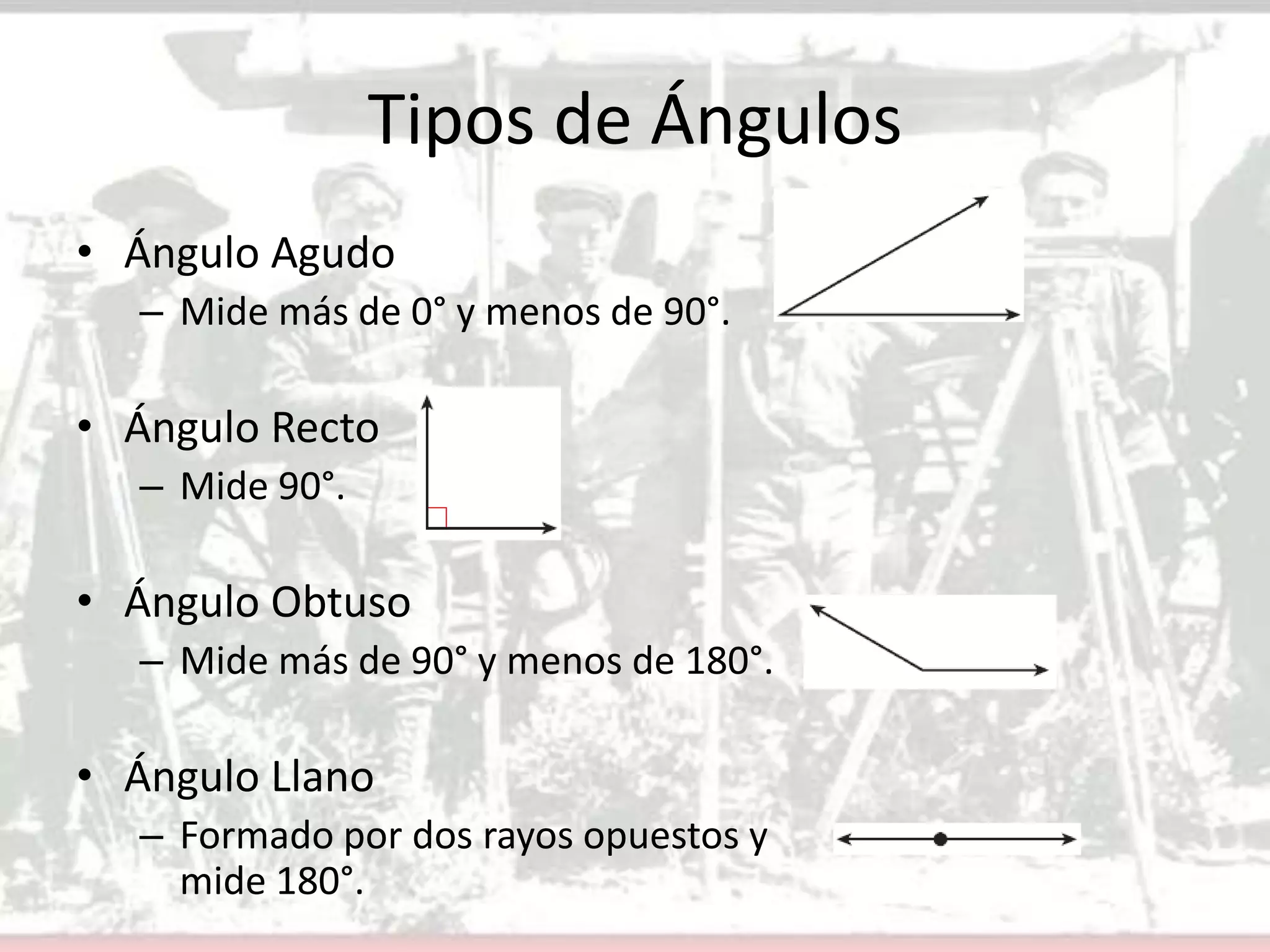
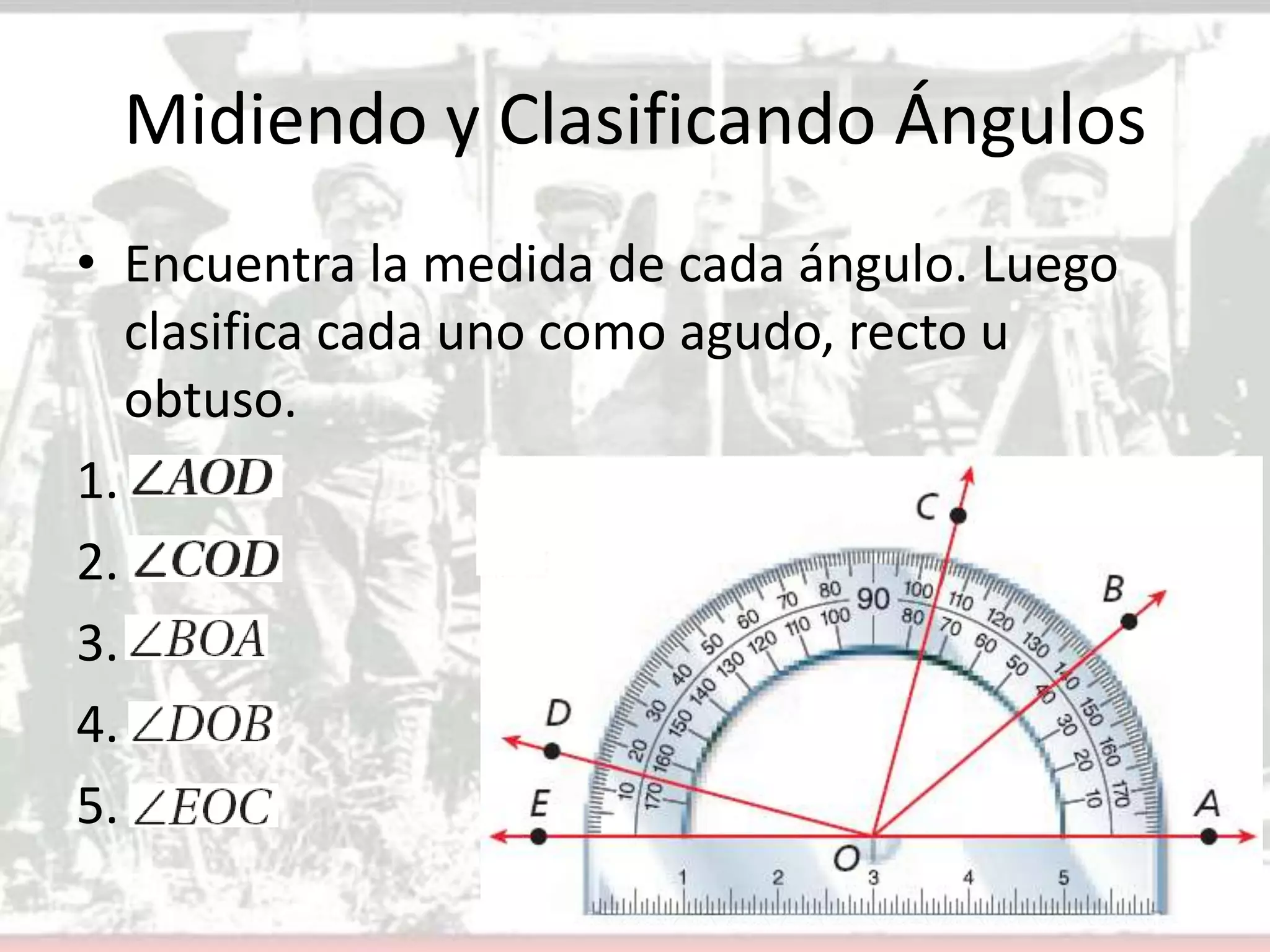
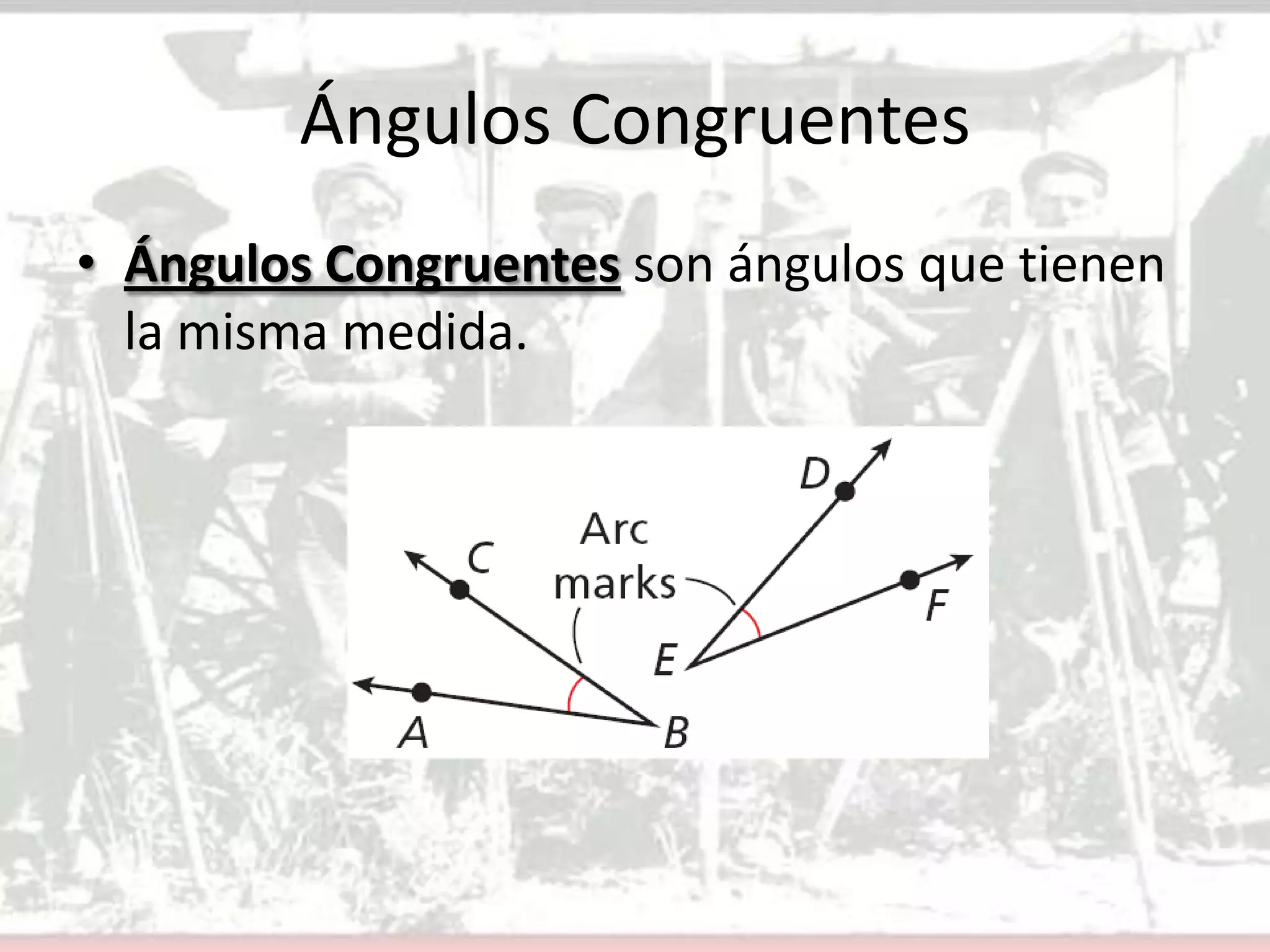
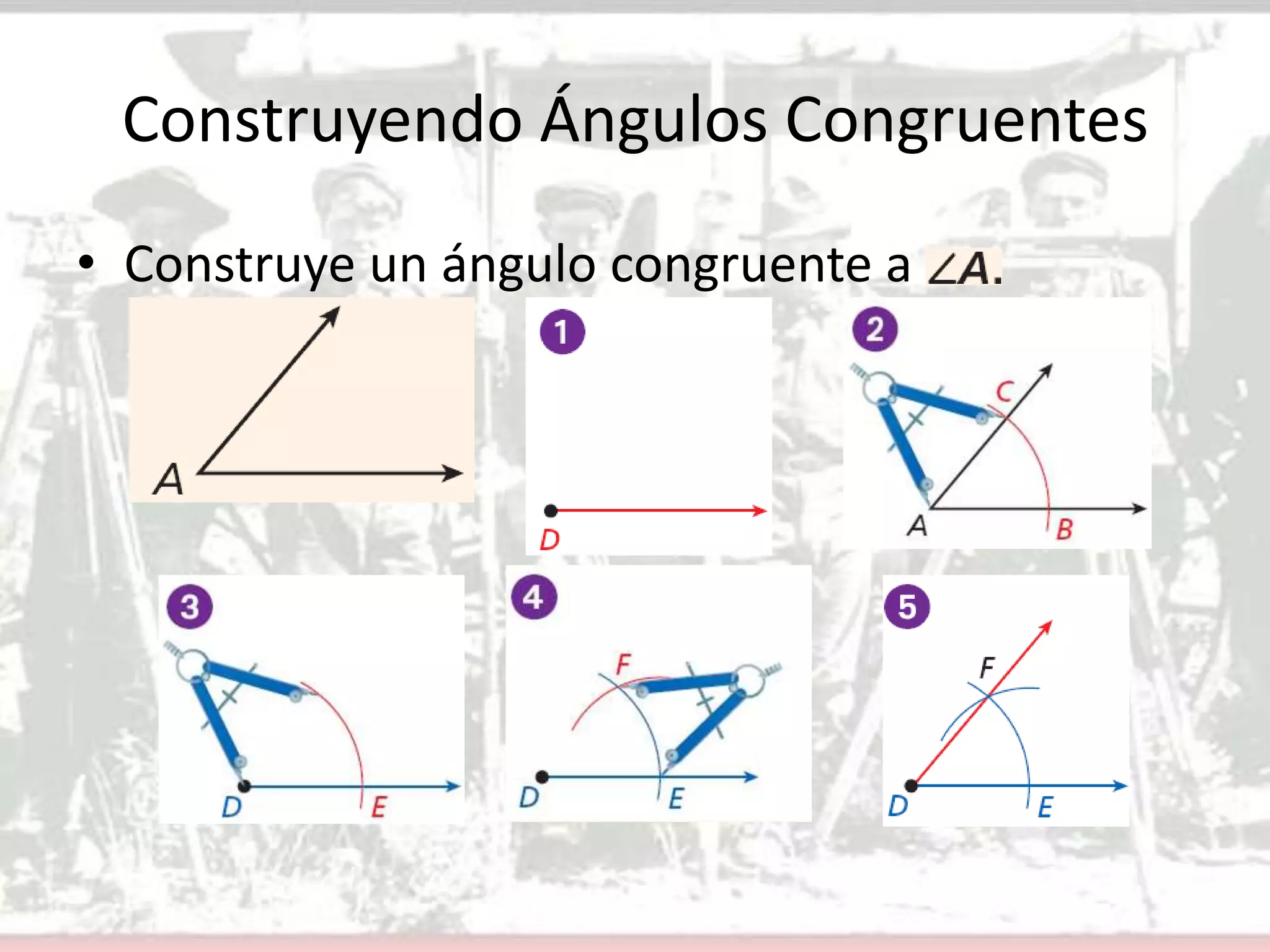
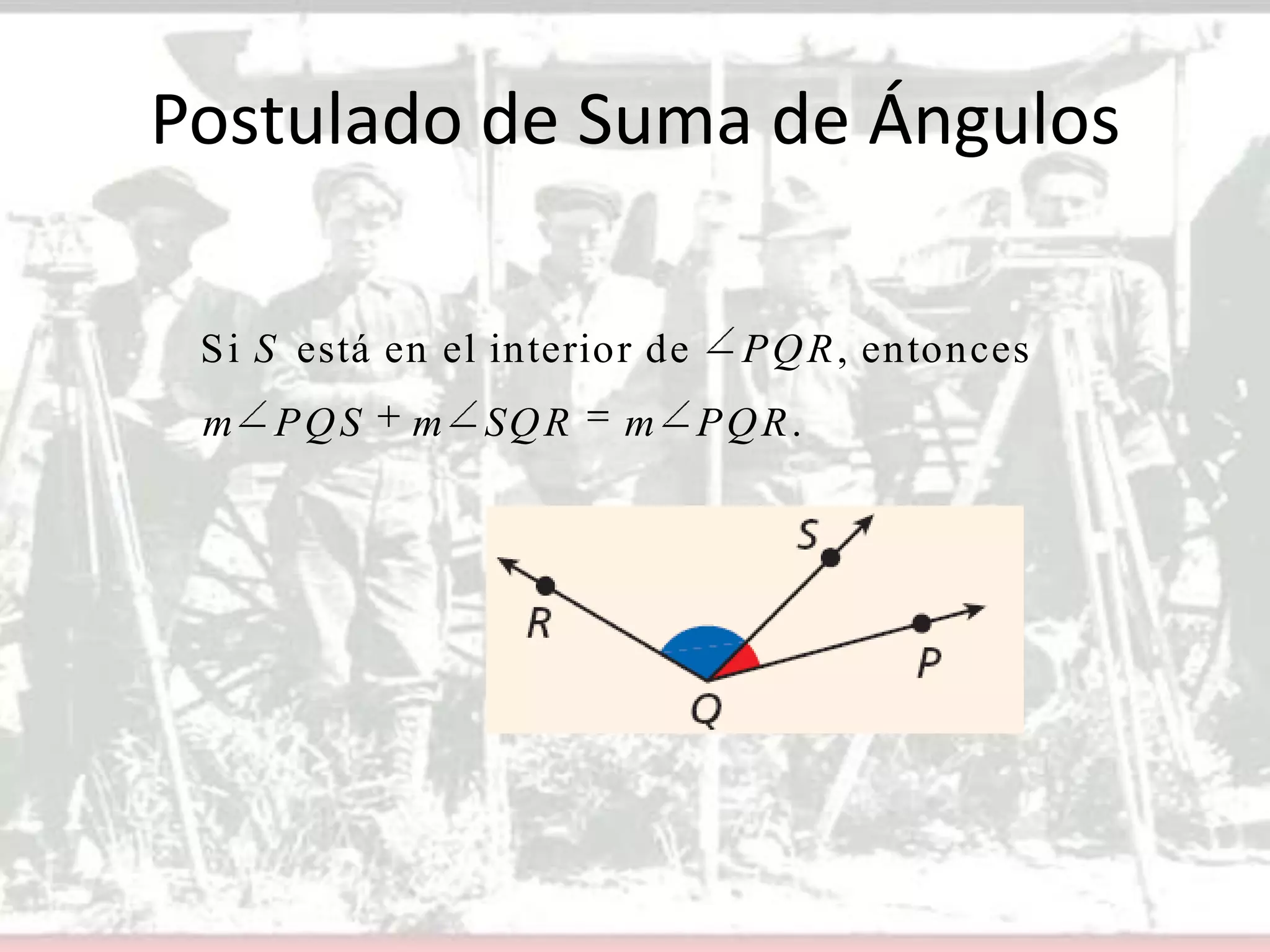
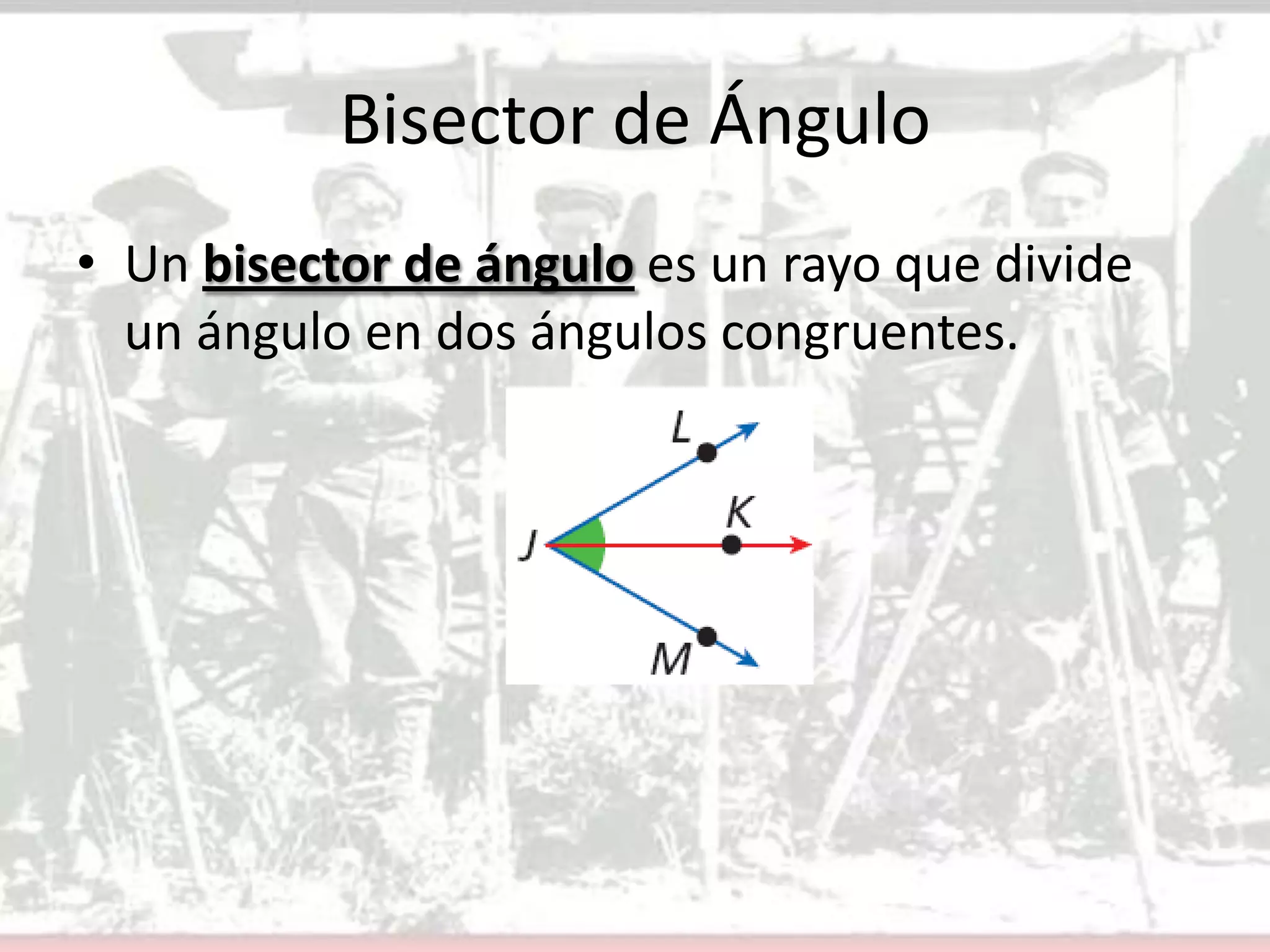
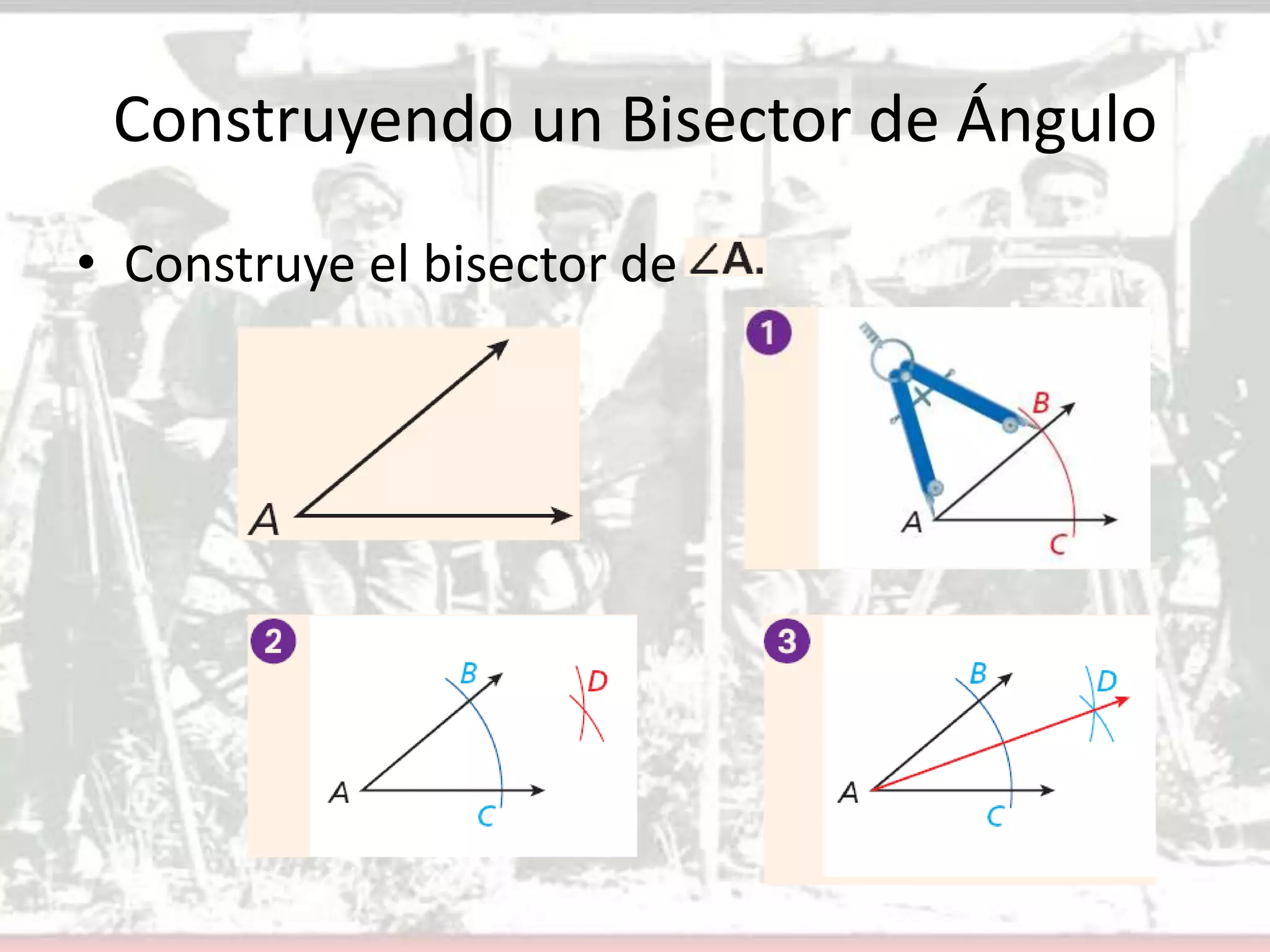
Este documento presenta conceptos básicos sobre ángulos en geometría. Define un ángulo, cómo se nombran y miden ángulos, y los diferentes tipos de ángulos (agudo, recto y obtuso). Explica cómo construir ángulos congruentes y bisectores de ángulos usando un transportador. Finalmente, asigna ejercicios para que los estudiantes apliquen estos conceptos.

1. Sección 1 – 3Midiendo y Construyendo ÁngulosGeometríaDécimo Grado

2. WARM UPDibuja AB y AC, donde A, B y C son no-colineales.Dibuja rayos opuestos DE y DF.Resuelve cada ecuación.3. 2x + 3 + x – 4 + 3x – 5 = 1804. 5x + 2 = 8x – 10

3. ObjetivosNombrar y clasificar ángulos.Medir y construir ángulos y bisectores de ángulos.

4. DefinicionesUn ángulo es una figura formada por dos rayos, o lados, con un extremo en común llamado el vértice.El conjunto de todos los puntos entre los lados del ángulo es el interior del ángulo.El exterior del ángulo es el conjunto de todos los puntos fuera del ángulo.Formas de nombrar el ángulo:

5. Nombrando ÁngulosUn agrimensor apuntó los ángulos formados por un “transit” (punto T) y tres puntos distantes Q, R y S. Nombra tres de los ángulos.

6. Postulado del TransportadorLa medida de un ángulo es usualmente dada en grados.Dado que hay 360° en un círculo, un grado es 1/360 parte de un círculo.Postulado del TransportadorDado AB y un punto O en AB, todos los rayos que pueden ser dibujados desde O pueden ser puestos en una correspondencia uno-a-uno con los números reales desde 0 hasta 180.

7. Transportador

8. Tipos de ÁngulosÁngulo AgudoMide más de 0° y menos de 90°.Ángulo RectoMide 90°.Ángulo ObtusoMide más de 90° y menos de 180°.Ángulo LlanoFormado por dos rayos opuestos y mide 180°.

9. ActividadMidiendo Ángulos con el Transportador

10. Midiendo y Clasificando ÁngulosEncuentra la medida de cada ángulo. Luego clasifica cada uno como agudo, recto u obtuso.Hhkk

11. Ángulos CongruentesÁngulos Congruentes son ángulos que tienen la misma medida.

12. Construyendo Ángulos CongruentesConstruye un ángulo congruente a

13. Postulado de Suma de Ángulos

14. Utilizando el Postulado de Suma de Ángulos

15. Bisector de ÁnguloUn bisector de ángulo es un rayo que divide un ángulo en dos ángulos congruentes.

16. Construyendo un Bisector de ÁnguloConstruye el bisector de

17. Encontrando la Medida de un Ángulo

18. AsignaciónPágina 25, ejercicios 12 – 30 (pares)