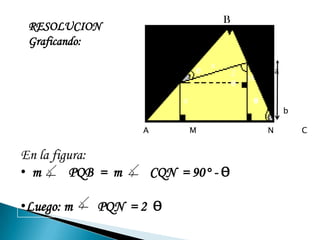
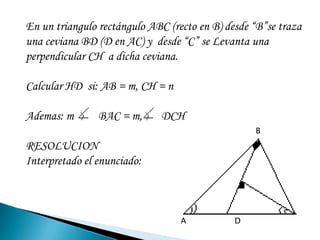
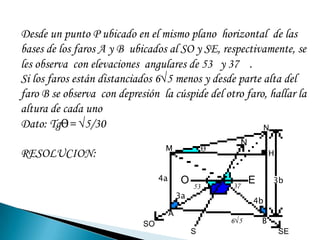
El resumen resume 6 problemas de trigonometría que involucran cálculos de ángulos y relaciones trigonométricas. El primer problema involucra calcular un ángulo dado tres relaciones trigonométricas. El segundo problema calcula la longitud PQ dada ángulos y lados en un triángulo rectángulo. El tercer problema calcula H dadas relaciones trigonométricas. El cuarto problema calcula HD dadas medidas en un triángulo con ceviana. El quinto problema calcula un ángulo trigonométrico dadas observaciones de alturas.

1. PROBLEMAS RESUELTOSRAZONES TRIGONOMETRICAS DE ANGULOS AGUDOSPROBLEMA 1

2. CALCULAR:Ѳ (agudo) si:Tg³ X Tg³ y Tg³z Tg³ Ѳ = 1Además : Sen (x + y) = Tg (z + y) Sec (x +2y) = Csc (y + 2x) Sec 3 (x +y - z) = Ctg (x – z +23º)

3. RESOLUCION:Del 3er. dato:(x +2y) + (y + 2x) = 90° x +y = 30 ° ……(1)En el 2do dato: Sen 30 ° = Tg (y + z)Tg (y + z) = ½ y + z = 26,5 ° ……(2)– (2): (x + y) - (y + z) = 30 ° - 26,5 ° x – z = 3,5 ° ……(3)

4. PROBLEMA 2

5. En un triangulo rectángulo:ABC (^B = 90° )Sobre los catetos AB y BC se ubican : P y Q respectivamente; si desde dichos puntos se trazan perpendiculares a la hipotenusa, PM = a y QN = b Hallar PQ en función de a,b y “ Ѳ” Además:m ACB = Ѳ, m BPQ = Ѳ (a‹ b)

6. BRESOLUCIONGraficando:QxѲPb- a2ѲHѲa abA M N CEn la figura: m PQB = m CQN = 90° - Ѳ

7. Luego: m PQN = 2 ѲDe P trazamos PH QN QH = b – aEn r PQH: X = (b - a) Sec 2Ѳ r

8. PROBLEMA 3

9. Si:Sen (a ∏/3) Sec (∏/2 – b ∏/3) = √3 Tg ∏/6Ademas: a = Csc Ѳ . Csc α b = Sec Ѳ . Sec αCalcular. H = √2 Sec (Ѳ + α/2)

10. RESOLUCION:En la 1ra, condicion por la propiedad del complemento se cumple que:Sec (∏/2 – b ∏/3) = Csc (b ∏/3)Reemplazando en el 1er dato:Sen ()a ∏/3) . Csc (b ∏/3) = 1 Y por propiedad de las R. T. reciprocas:A ∏/3 = b ∏/3 a = b ……….(1)Reemplazando la 2da y 3ra condicion en (1)Csc Ѳ . Csc α = Sec Ѳ . Sec α

11. Csc α/Sec α = SecѲ/CscѳCos α/Sen α = SenѲ/CosѲCtg α = TgѲ(propiedad R. t. complementarias)Α + Ѳ = 90⁰Luego en H:H= √2 Sec (90°/2) = √2 Sec45°H= 2

12. Y (2) en el 4to dato:Sec 3 (30 - z°) = Ctg (3,5° + 23 ° )Sec (90 ° - 3z ) = Ctg 26,5 ° = 2Csc 3z = 2 30 ° z = 10 ° Pero, de (1) : y = 30 ° - zEn el 1er dato del problemaTg 3x tg(90 ° - 3x) tg 30 ° tg 3 Ѳ = 1Ctg 3 x 1Tg 3 Ѳ = √3 3 Ѳ = 60 ° Ѳ = 20 ° 3/3 Tg 3Ѳ = 1

13. PROBLEMA 4

14. En un triangulo rectángulo ABC (recto en B) desde “B”se trazauna ceviana BD (D en AC) y desde “C” se Levanta una perpendicular CH a dicha ceviana.Calcular HD si: AB = m, CH = nAdemas: m BAC = m, DCHRESOLUCION Interpretado el enunciado:BmHXnααA D C

15. De la figura, sea: m BAD = m HCD = αEn r HDC: x = n TG α ……(1) HD En r ABC : bc= m Tg αObservación:m BDC = m BCD = 90° - αLuego: BDC: isoceles BD = BC = m Tg αEntonces: BH = BD – HD BH = mn TG αEn r BHC: por pitagoras

16. BC² = BH² + HC²m² Tg² α = (m - n) ² Tg² α + n²De donde:Tg²α = √n/2m – n …….(2)(2) En (1): x = n √n/2m-n

17. PROBLEMA 5

18. Desde la parte mas alta de un acantilado de H m de la altura, se observa un globo con un ángulo de elevación, igual a “Ѳ” ; desde un punto ubicado en la superficie del acantilado , se observa el globo con un ángulo de elevación igual a “α” y la parte mas alta del acantilado con un ángulo de elevación igual a 26° 30َ.Calcule Tgα (Ctg Ѳ - 1) . Si además el globo se encuentra a una altura igual a 3 H mRESOLUCION:E3HAѲQHαα53°/2DBC

19. rr ABC : notable(53 /2 ) Si : AB =H BC = 2H rr CED : CD = 3H CtgαCuadrilátero AQDB:AB=QD = H EQ = 2 Hr AEQ : AQ= EQ CtgѲ AQ = 2H Ctg ѲPero: AQ = BD AH Ctg Ѳ = 2H+3H Ctgα2Ctg Ѳ = 2+3 Ctgα2(Ctg Ѳ - 1) =3CtgαTgα(CtgѲ - 1) =3/2 r

20. Problema6

21. Desde un punto P ubicado en el mismo plano horizontal de las bases de los faros A y B ubicados al SO y SE, respectivamente, se les observa con elevaciones angulares de 53° y 37 ° .Si los faros están distanciados 6√5 menos y desde parte alta del faro B se observa con depresión la cúspide del otro faro, hallar la altura de cada unoDato: TgѲ= √5/30RESOLUCION:NNMѲHOE4a3b37 °53°3a4bA6√5 BSOSSE

22. Del dato : Tg Ѳ = √5 /30 = NH/MH 5/30 = NH/ 6√5 ->NH=1Pero: BH:4ª->3b =4ª +1 …(*)Además: (3a)² + (4b)² = (6√5 )² 9a² + 16b² = 180Multiplicado por 9: 81 a² + 16b(3 b)² =1620Reemplazando (*): 81a² + 16 ( 4a + 1)² = 1620 81a² + 256a² +128a + 16 =1620 336a² + 128a - 1620 = 0

23. Aspa simple:337a 802 a -2->a – 2 = 8 ->a = 2Luego:Faro A: 4ª = 8 FaroB:4ª + 1 =9 Alturas : 8 y 9