Variograma

ContenidoContenido
• VARIOGRAMA EXPERIMENTAL
• VARIOGRAMA TEÓRICO
• Propiedades básicas
• Definición
• Estudio de modelos de variograma
• Cálculo a partir de los datos
• Características básicas
• Definición
• Ajuste de modelos de variograma

Variograma Teórico-DefiniciónVariograma Teórico-Definición
Es una herramienta que permite
analizar el comportamiento espacial
de una propiedad o variable sobre
una zona dada
Detectar direcciones de anisotropía
Ejemplo:
Zonas de influencia y su extensión (correlación
espacial)
Variabilidad con la distancia

1
5
3
7
9
8
2
4
6 1
2
3
4
5
6
7
8
9
A B
MEDIA = 5
0
2
4
6
8
10
12
0 1 2 3 4
Distancia
Variograma
0
2
4
6
8
10
12
0 1 2 3 4
Distancia
Variograma
VARIANZA=50/9
HISTOGRAMAS IGUALES
Continuidad espacial

0
0,02
0,04
0,06
0,08
0,1
0,12
0 2 4 6 8 10
Distancia
Variograma
0
0,2
0,4
0,6
0,8
1
0 5 10 15 20 25
Ubicación
Variable
0
0,2
0,4
0,6
0,8
1
1 2 3 4 5 6 7
Distancia
Variograma
-1
-0,5
0
0,5
1
1,5
2
1 3 5 7 9 11 13 15 17 19
Ubicación
Variable Variograma Teórico-DefiniciónVariograma Teórico-Definición

0
0,002
0,004
0,006
0,008
0,01
0,012
1
3
5
7
9
11
13
15
17
19
Distancia
Variograma
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
1
3
5
7
9
11
13
15
17
19
21
23
25
Ubicación
Variable Variograma Teórico-DefiniciónVariograma Teórico-Definición

Curva de proporción vertical
Unidad 2 Unidad-5
Unidad 1 Unidad-4

Curva de proporción vertical

2
)]()([
2
1
hxZxZE +−=
)]()([
2
1
)( hxZxZVarh +−=γ
nn
RhRx ∈∈ ,
)(xZ es estacionaria o intrínsecaSi

γ• depende del módulo y de la dirección del vector h
Variograma Teórico-CaracterísticasVariograma Teórico-Características
( ) 2
)]()([
2
1
hxZxZEh +−=γ
• Valor promedio de la diferencia al cuadrado de los
valores de la propiedad en dos puntos separados por
una distancia |h|
γ• es independiente de la localización x

( )hxZ +
1hx +
h
1h
( )1hxZ +
hx+
( ) 2
2
1
)]()([ hxZxZEh +−=γ
( )xZ
x
Detección de
características
que varían según
la dirección y la
distancia

Distancia
Variograma
Distancia
Variograma

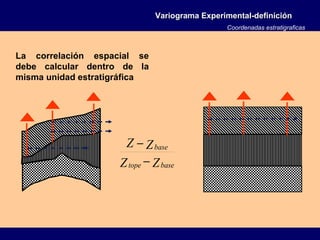
Variograma Experimental-definiciónVariograma Experimental-definición
( ) 2
2
1
)]()([ hxZxZEh +−=γ Variograma Teórico
Variograma Experimental
( ) ∑
=−
−=
hxx
ji
ji
xzxz
hN
h 2*
))()((
2
1
)(γ

ZZ
ZZ
basetope
base
−
−
Variograma Experimental-definiciónVariograma Experimental-definición
Coordenadas estratigraficas
La correlación espacial se
debe calcular dentro de la
misma unidad estratigráfica

( ) ∑
=−
−=
hxx
ji
ji
xzxz
hN
h 2*
))()((
2
1
)(γ
• Se escoge una dirección θ
• Se escoge una distancia o lag h
• Se calcula para valores de h,2h,
3h,...,nh
*
γ
• Se grafica versus los valores
h,2h, 3h,...,nh
*
γ
0
1
2
3
4
5
6
0
0.4
0.8
1.2
1.6
2
2.4
2.8
3.2
3.6
4
Distancia
variogramaexperimental
Variograma
experimental
Variograma Experimental-obtenciónVariograma Experimental-obtención

( ) ∑=
+−=
)(
2*
))()((
2
1
)(
hN
1i
ii hxzxz
hN
hγ
( ) ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) ( ) ( )( )[ ]2
65
2
54
2
43
2
32
2
21
*
5*2
1
xzxzxzxzxzxzxzxzxzxzh −+−+−+−+−=γ
( ) ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) ( ) ( )( )[ ]2
64
2
53
2
42
2
31
*
4*2
1
2 xzxzxzxzxzxzxzxzh −+−+−+−=γ
( ) ( ) ( )( ) ( ) ( )( ) ( ) ( )( )[ ]2
63
2
52
2
41
*
3*2
1
3 xzxzxzxzxzxzh −+−+−=γ
1x 2x 3x 4x 5x 6x
h
Datos Igualmente espaciados:

h
Datos Igualmente espaciados:
( ) ∑=
+−=
)(
2*
))()((
2
1
)(
hN
1i
ii hxzxz
hN
hγ
( ) ,2,1,0,,0 =kkh
( ) ,2,1,0,0, =kkh
( ) ,2,1,0,,, ±±=jkjhkh

Datos Irregularmente espaciados:
• Puede ocurrir que no existan valores de la variable a la distancia h
• Puede ocurrir que no existan valores de la variable en la dirección θ

Variograma Experimental-distanciaVariograma Experimental-distancia
• Clases de distancia:
Para cada lag h se define una tolerancia y se utilizan
únicamente los puntos que se encuentran a una distancia mayor o
igual a y menor que
h∆
hh ∆− hh ∆+
( )3xz
h
2h
3h
( )1xz
( )2xz
( )4xz
( )5xz

• Clases de distancia:
h∆El valor de se escoge como el 50% del valor del
lag h. De esta forma:
• Las clases de distancia no se superponen
• No hay valores de la variable fuera de una clase de
distancia

0 1 2 3 4 5 6
1.20 2.4 2.8 4.9
1.20 2.4 2.8 4.9
5.0=∆h
1=h
1=∆h
1=h
1.20 2.4 2.8 4.9
1.0=∆h
1=h

hh 5.0>∆
hh 5.0=∆
hh 5.0<∆

• Clases de dirección :
θθ ∆− θθ ∆+
θ∆θPara cada dirección se define una tolerancia
y se utilizan únicamente los puntos que se
encuentran entre las direcciones y
Variograma Experimental-direcciónVariograma Experimental-dirección

θθ ∆−
θθ ∆+
puntos descartados
puntos aceptados
θ
θ∆

θ
θθ ∆−
θθ ∆+
θ∆
puntos aceptados
puntos descartados
b
b = ancho de banda

Variograma Experimental-distancia & direcciónVariograma Experimental-distancia & dirección
clase de distancia h
h
2h
3h
θ
θ∆
clase de distancia
2h
clase de distancia
3h
z(x)

θ
θ θ

h: Distancia promedio entre los pozos
A partir del variogram cloud
A partir del variograma omnidireccional
Se escoge como la dirección de anisotropía
de la variable. Se puede obtener a partir
de:
Información geológica, petrofísica, etc
Mapa de variograma
θ:
n: Cuando se calcula el variograma sobre un
dominio D se escoge n de forma tal que:
n*h < | D | / 2
Valor del lag h
Número n de lags
Valor de θ θ∆y

1.20 2.4 2.8 4.9
Lag h muy grande
Lag h pequeño, n muy grande
Variograma Experimental-Variograma Experimental-laglag
1.20 2.4 2.8 4.9
Lag h adecuado, valor de n ?

Variograma Experimental-Variograma Experimental-laglag

Variograma OmnidireccionalVariograma Omnidireccional
Variograma Omnidireccional:
Es aquel que no depende de la dirección
Se obtiene al escoger la tolerancia angular θ∆
de forma tal que las direcciones θθ ∆+ y θθ ∆−
sean opuestas y perpendiculares a la dirección θ
Se puede pensar como el promedio del variograma
experimental en todas las direcciones posibles

Variograma direccional
Variograma omnidireccional
Variograma OmnidireccionalVariograma Omnidireccional

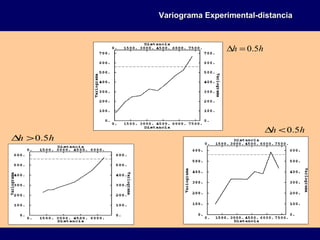
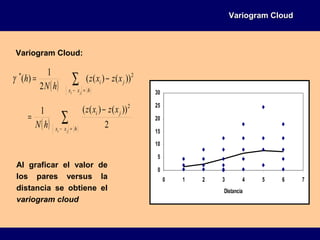
Variogram CloudVariogram Cloud
( ) ∑
=−
−=
hxx
ji
ji
xzxz
hN
h 2*
))()((
2
1
)(γ
Variogram Cloud:
( ) ∑
=−
−
=
hxx
ji
ji
xzxz
hN 2
))()((1
2
Al graficar el valor de
los pares versus la
distancia se obtiene el
variogram cloud
0
5
10
15
20
25
30
0 1 2 3 4 5 6 7
Distancia

Variogram Cloud:
Permite detectar valores
atípicos o cambios bruscos
Permite escoger un valor
inicial del lag
Permite observar la dispersión
alrededor del valor de
*
γ 0
50
100
150
200
250
300
0 1 2 3 4 5 6 7
Distancia

Mapa de VariogramaMapa de Variograma
Mapa de Variograma :
Es una herramienta que
permite determinar las
direcciones de anisotropía
de la variable en estudio

0
0
Definir una malla (2n+1)*(2n+1)
h
Definir el valor del lag h
Asignar a cada bloque el valor
de
*
γ

Variograma Experimental-tolerancia angularVariograma Experimental-tolerancia angular
Tolerancia angular

Variograma-Características Básicas
1) RANGO Y SILL
2) COMPORTAMIENTO A PEQUEÑAS DISTANCIAS
3) COMPORTAMIENTO A GRANDES DISTANCIAS
4) ANISOTROPÍAS

0
0,5
1
1,5
2
2,5
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
Distancia
Variograma
Rango:
Distancia a la cual el
variograma se estabiliza
Sill :
Valor constante que toma el
variograma en distancias
mayores al rango
Variograma-Rango & Sill

( ) )]()([)]()([
2
1 22
hxZxZEhxZxZEh +−=+−= σγ
Si para una distancia dada d las variables Z(x) y
Z(x+h) son no correlacionas entonces el variograma
es constante
2
σ=
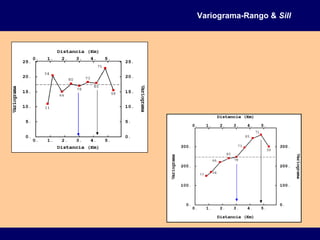
Rango:
Distancia a partir de la cual
no hay correlación
Sill:
Varianza de la función aleatoria Z
Variograma-Rango & Sill

COMPORTAMIENTO A PEQUEÑAS DISTANCIAS
Comportamiento
1) DISCONTINUO
2) LINEAL
3) CUADRÁTICO
Permite estudiar cuán rápido puede variar la
variable en estudio a pequeñas distancias.
Básicamente el variograma presenta las 4 formas
siguientes:
4) HÍBRIDOS

Comportamiento discontinuo
( ) )]()([
2
1
hxZxZvarh +−=γ
( ) 00 =γ
Puede ocurrir que para
distancias cercanas a cero el
valor del variograma no se
aproxima a cero
Efecto pepita o nugget effect

Interpretación del nugget effect
1) Variable muy irregular a distancias cortas
( ) 2
)]()([
2
1
hxZxZEh +−=γ
0≈h
Z(x) y Z(x+h) difieren mucho
no se aproxima a cero

0
0,5
1
1,5
2
2,5
3
3,5
0
1,5
3
4,5
6
7,5
9
10,5
12
13,5
15
16,5
18
Distancia
Variograma Valores
observados
Valores
reales
2) Errores de medición en
las variables
( ) ( ) ( )xxZxZobs ε+=
( ) ( ) 2
εσγγ += hh ZZobs
2
εσ

3) presencia de estructuras o
ausencia de valores en distancias
inferiores a las que se tomaron las
muestras

Comportamiento Lineal
Comportamiento lineal
Indica que para
distancias pequeñas, el
variograma tiene un
comportamiento lineal.
Representa variables
continuas pero no
diferenciables. Así, la
propiedad puede
cambiar rápidamente
de un punto a otro.
0
0,5
1
1,5
2
2,5
3
3,5
0
1,5
3
4,5
6
7,5
9
10,5
Distancia
Variograma

Comportamiento lineal
La variabilidad de la
propiedad dependerá de
la pendiente de la recta
en el origen
A mayor pendiente,
mayor variabilidad
A menor pendiente,
menor variabilidad
0
0,5
1
1,5
2
2,5
3
3,5
0 1 2 3 4 5 6 7 8 9 10 11
Distancia
Variograma
0
0,5
1
1,5
2
2,5
3
0 1 2 3 4 5 6 7 8 9 10 11
Distancia
Variograma
Comportamiento Lineal

Comportamiento Cuadrático
Comportamiento Cuadrático
Indica que para distancias
pequeñas, el variograma tiene
un comportamiento cuadrático.
Representa variables sumamente
continuas e infinitamente
diferenciables. Así, la propiedad
NO puede cambiar rápidamente de
un punto a otro. 0
0,5
1
1,5
2
2,5
3
3,5
1
4
7
10
13
16
19
22
25
28
31
34
37
Distancia
Variograma

0
1
2
3
4
5
6
7
8
0 1,5 3 4,5 6 7,5 9 10,5 12 13,5 15 16,5 18
Distancia
Variograma
Comportamiento Híbrido:
Variación más suave a
distancias cortas
Variación más fuerte a
distancias grandes
Indica presencia de
estructuras actuando a
diferentes escalas
Comportamiento Híbrido

Comportamiento-grandes distancias
NO TODOS LOS VARIOGRAMAS
POSEEN UN RANGO Y UN SILL
FINITO
Distancia
Variograma
INDICA LA PRESENCIA DE
UNA DERIVA O DRIFT
VARIABLE NO ESTACIONARIA
Comportamiento a grandes
distancias :

( )( ) ( )xmxZE =
Drift
( ) ( ) ( )[ ] ( ) ( )[ ]22
2
1
2
1
xmhxmxZhxZEh −+−−+=γ
Variograma Teórico
Estimación del variograma
Sesgo

D1=E-O
D2=N-S

Anisotropías
Anisotropías :
Generalmente cuando el variograma
experimental es calculado en distintas
direcciones presenta distintos comportamientos
con la variación de la distancia.
Anisotropía Geométrica
Anisotropía Zonal
Anisotropía Híbrida

Anisotropía Geométrica :
Es aquella en la que el
variograma en distintas
direcciones presenta el
mismo sill pero rangos
distintos
0
0,5
1
1,5
2
2,5
3
0,0 0,9 2,0 3,0 4,1 5,1 6,2 7,2 8,3 9,3 10,4 11,4
Distancia
Variograma
N-S
E-O
Mayor continuidad espacial
en la dirección de mayor
rango
Menor continuidad espacial
en la dirección de menor
rango

0
0,5
1
1,5
2
2,5
3
0,0 0,9 2,0 3,0 4,1 5,1 6,2 7,2 8,3 9,3 10,4 11,4
Distancia
Variograma
N-S
E-O

Anisotropía Zonal :
direcciones presenta el
mismo rango pero diferente
sill
Presencia de diferentes
estructuras
0
0,5
1
1,5
2
2,5
3
3,5
0 0,94 1,99 3,04 4,09 5,14 6,19 7,24 8,29 9,34 10,4 11,4
Distancia
Variograma
Anisotropía Zonal

0
0,5
1
1,5
2
2,5
3
3,5
0 0,94 1,99 3,04 4,09 5,14 6,19 7,24 8,29 9,34 10,4 11,4
Distancia
Variograma
Anisotropía Zonal

Anisotropía Híbrida :
direcciones presenta
rangos diferentes y
distintos sill.
Presencia de diferentes
estructuras
Característico de variogramas
horizontales y verticales
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
0 0,6 1,2 1,8 2,4 3 3,6 4,2 4,8 5,4 6 6,6 7,2
Distancia
Variograma
Anisotropía Híbrida

COVARIANZA VS VARIOGRAMA
• El variograma se puede utilizar para modelar
fenómenos no estacionarios y la covarianza no, por
el desconocimiento de la media.
• Cuando la media es constante pero desconocida
no se necesita para el cálculo del variograma, pero
si para el de la covarianza.
•Si la función tiene varianza infinita (no estacionaria)
la covarianza no está definida en 0, sin embargo el
variograma si y es idénticamente nulo

Comentarios
CORRELACIÓN VS VARIOGRAMA
• La correlación estadística usual es
calculada a distancia cero (dos
observaciones en el mismo punto
del espacio) y puede no ser
representativa
• El variograma toma en cuenta el
espaciamiento y por lo tanto permite
”correlacionar espacialmente”
Fuente información 1
Fuente información 2

LIMITACIONES DEL VARIOGRAMA
• Es un estadístico de 2 puntos
Comentarios
• Utilizar técnicas multipuntos y
reconocimiento de patrones

LIMITACIONES DEL VARIOGRAMA
Comentarios
• Es extremadamente
sensible a valores
extremos
7
10
11
12
25
14
12
13
2
11
9
8
7
10
11
12
13
14
12
13
10
11
9
8
0
10
20
30
40
50
60
1 2 3 4 5 6
Distancia
Variograma
0
2
4
6
8
1 2 3 4 5 6
Distancia
Variograma

DEL VARIOGRAMA
EXPERIMENTAL AL
MODELO DE VARIOGRAMA
*
γ
γ

Ajustar
POR QUE HAY QUE CONSTRUIR
MODELOS DE VARIOGRAMA ?
0
1
2
3
4
5
6
0
0.4
0.8
1.2
1.6
2
2.4
2.8
3.2
3.6
4
Distancia
variogramaexperimental
Variograma
experimental
0
1
2
3
4
5
6
0
0.4
0.8
1.2
1.6
2
2.4
2.8
3.2
3.6
4
Distancia
Variograma
experimental
Modelo de
variograma
El variograma experimental no
se puede evaluar en distancias
o direcciones intermedias
Una interpolación entre los puntos del
variograma experimental no garantiza la
existencia y unicidad de la solución del
sistema de kriging
La interpolación no satisface las
condiciones que todo variograma debe
satisfacer
El variograma experimental no satisface
las condiciones que todo variograma
debe satisfacer
*
γ

Variograma Teórico-propiedades
LOS VARIOGRAMAS TIENEN PROPIEDADES ESPECIALES, CUALQUIER FUNCIÓN QUE
DEPENDA DE LA DISTANCIA Y LA DIRECCIÓN NO NECESARIAMENTE ES UN
VARIOGRAMA
1) ( ) 00 =γ
2) ( ) ( )hh γγ =−
El variograma calculado en la dirección de h es igual al variograma
calculado en la dirección de -h
h-h

3) Todo variograma es una funcion definida positiva condicional
Para cualquier n, cualesquiera nxxxx ,,,, 321  puntos en el espacio y cualesquiera
nλλλλ ,,,, 321 valores tales que ∑=
=
n
i
i
1
0λ se tiene que
( ) 0
1 1
≥−− ∑∑= =
n
i
n
j
jiji xxγλλ
Esta propiedad permite calcular en forma consistente la varianza de combinaciones
lineales de funciones aleatorias
( ) αβ
βα
α
α
γλλλ −=Zvar

4) Relación con la función de covarianza
Para funciones aleatorias estacionarias se tiene que ( ) ( ) ( )hCCh −= 0γ
Distancia
Variograma
Variograma
Covarianza

( ) 02
=
∞→ h
h
lim
h
γ
4) Si γ es el variograma de una funcion aleatoria estacionaria o intrínseca entonces
En particular para h suficientemente grande existe una constante c tal que ( ) 2
hch ≤γ
Criterio para el comportamiento del variograma a grandes distancias
Criterio para detectar un comportamiento no estacionario

4) Combinacion lineal de variogramas
( ) ( ) ( ) ( )hhhh Nγγγγ ,,,, 321 Si son modelos de variograma y αααα N,,,, 321 
son valores positivos entonces
( ) ( )hh
n
i
i i∑=
=
1
γαγ
Permite modelar/ajustar las estructuras imbricadas (nested structures)
Permite modelar la anisotropía zonal

0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 1.3 2.6 3.9 5.2 6.5 7.8 9.1 10.4 11.7 13 14.3 15.6 16.9
0
0.5
1
1.5
2
2.5
0 1.3 2.6 3.9 5.2 6.5 7.8 9.1 10.4 11.7 13 14.3 15.6 16.9
0
0.5
1
1.5
2
2.5
0 1.3 2.6 3.9 5.2 6.5 7.8 9.1 10.4 11.7 13 14.3 15.6 16.9
+ =

Modelar la anisotropía zonal
0
0,5
1
1,5
2
2,5
3
3,5
0 0,94 1,99 3,04 4,09 5,14 6,19 7,24 8,29 9,34 10,4 11,4
Distancia
Variograma
( ) =hγ ( )211 ,hhγ ( )32 hγ+

Modelos de Variograma
Modelos de variograma isotrópicos más comunes:
Modelo Efecto Pepita Puro
Modelo Esférico
Modelo Exponencial
Modelo Gaussiano
Modelo Cúbico
Modelo Seno Cardinal
Modelo Potencia

Modelo Efecto Pepita Puro
S
Distancia
Variograma










≠
=
=
0
00
hsis
hsi
hγ
Este modelo representa a
un fenómeno
completamente aleatorio, en
el cual no hay correlación
espacial
No importa cuán cerca se
encuentren los valores de
las variables, siempre serán
no correlacionados

Modelo Esférico






























>
≤−
=
ahsis
ahsi
a
h
a
h
s
h
3
3
2
1
2
3
γ
Comportamiento lineal en el origen
Distancia
Variogramaas /5.1Pendiente igual a
Es uno de los modelos de
variograma más utilizados
Rango s y sill a
Representa fenómenos continuos
pero no diferenciables

Modelo Exponencial
( ) 















−−=
a
h
sh exp1γ
DistanciaVariograma
Sill s que alcanza asintóticamente
Rango aparente igual a a
Rango experimental igual a 3a
as /3Pendiente igual a
pero no diferenciables
Comportamiento lineal en el origen

Modelo Gaussiano
( ) 















−−=
a
h
sh 2
2
exp1γ
Distancia
Variograma
Rango experimental igual a a3
Comportamiento cuadrático en el origen
infinitamente diferenciables (sumamente
continuos)

Modelo Cúbico






























>
≤−+−
=
ahsis
ahsi
a
h
a
h
a
h
a
h
s
h
7
7
5
5
3
3
2
2
75.05.375.87
γ
Rango a y sill s
Representa fenómenos bastante continuos
Distancia
Variograma

Modelo Seno Cardinal
( )
( )








−=
ah
/ah
sh
/
seno
1γ
Distancia
Variograma
Rango experimental igual a 3a
Se utiliza para representar fenómenos
continuos con periodicidades

Modelo Potencia
( ) p
hsh =γ
Distancia
Variograma
s=2.5, p=0.4
s=0.4, p=1.8
s=1.15, p=1
s se denomina factor de escala
20 <≤ p
El comportamiento en el origen
depende del valor de p
Representa fenómenos no
estacionarios

DE MODELOS ISOTRÓPICOS
A MODELOS
ANISOTRÓPICOS
γ

Modelo Anisotrópicos
( )h1γ Variograma isotrópico de sill 1 y rango 1
( ) 







+= 2
2
2
2
1
y
y
x
x
R
h
R
h
sh γγ Variograma anisotrópico de sill s con rango xR
en la dirección del eje X y rango yR en la dirección
del eje Y
xR
yR
X
Y
Los ejes de anisotropía coinciden con los
ejes de coordenadas

X
Y
Modelo Anisotrópicos
Los ejes de anisotropía NO coinciden con los
ejes de coordenadas
xR
yR
X’
Y’
θ
1) Transformar los puntos del sistema
de coordenadas XY al sistema de
coordenadas X’Y’
Rhh =' R= matriz de rotación
T
2) Proceder como antes para ajustar la
longitud de los ejes de anisotropía
'Th = matriz para transformar
las distancias
3) Evaluar el variograma isotrópico en el
resultado.
( ) ( )TRhsh 1γγ =
Es un variograma anisotrópico en la dirección θ
con eje mayor igual a xR y eje menor igual a yR

VARIOGRAMA CRUZADO
comportamiento espacial en conjunto
ZYγ

Variograma Cruzado
Si Z, Y son funciones aleatorias estacionarias o intrínsecas, el variograma
cruzado de ellas se define como :
))]()(())()([(
2
1
)( hxYxYhxZxZEhZY +−+−=γ
( )
))()(())()((
2
1
)(*
ji
hxx
jiZY xyxyxzxz
hN
h
ji
−−= ∑
=−
γ
Para su estimación se utiliza el variograma cruzado experimental

Variograma Cruzado-propiedades
1) ( ) 00 =ZYγ
2) ( ) ( )hh ZYZY γγ =−
3) ( ) ( )hh YZZY γγ = El variograma cruzado es una función simétrica
4) Relación con la función de covarianza cruzada
( ) ( ) ( )( )hChCCh YZZYZYZY +−=
2
1
0)(γ
( ) ( )( ) ( )( )[ ]YZZY mhxYmxZEhC −+−=

4) Desigualdad de Hölder
( ) ( ) ( )hhh YZZY γγγ ≤2
El modelo de variograma cruzado no puede ser escogido independientemente de
cada uno de los variogramas individuales
Consecuencias:
El producto de cada uno de los sill de los variogramas individuales es mayor que el
cuadrado del sill del variograma cruzado
YZZY SSS ≤2

( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )hwhwhwh
hvhvhvh
huhuhuh
mmYZ
mmY
mmZ
γγγγ
γγγγ
γγγγ
+++=
+++=
+++=



2211
2211
2211
4) Modelo lineal de coregionalización
0>ju 0>jv 02
>− jjj wvu
mjj ,,1, =γ modelos de variogramas
Permite modelar en forma consistente el variograma cruzado y los variogramas
individuales

VARIOGRAMA DE
FUNCIONES INDICADORAS
Fγ
Modelando el comportamiento
espacial de Facies

Funciones Indicadoras
La función indicadora de la facies F se define como
( )




 ∈
=
nosi
Fxsi
xF
0
1
1
Si se considera la facies F como un conjunto aleatorio entonces su función indicadora es una
función aleatoria que puede ser estacionaria o no.
En lo sucesivo asumiremos que la función indicadora de F es estacionaria
( ) ( ) ( )( )2
11
2
1
xhxEh FFF −+=γ

Propiedades
1) ( )( ) [ ]1,0)(1 ∈=∈= pFxPxE F
( )( ) ( )ppxF −= 11var
2) ( ) 5.0≤hFγ
El sill de variogramas de funciones indicadoras no puede ser mayor a 0.5
3) Relación con la función de covarianza
( ) ( ) ( )hCCh FFF
−= 0γ
( ) ( )[ ] ( )[ ]( )pxphxEhC FFF −−+= 11
( ) ( )( ) ( ) 25.0110 ≤−== ppxC FF var

( ) ( ) ( )2121 hhhh FFF γγγ +≤+
4) Desigualdad Triangular
En particular ( ) ( )hh FF γγ 22 ≤
Consecuencia :
Un variograma con comportamiento en el origen de la forma 1>ph
p
no puede ser el variograma de una función indicadora

( ) )( FhxyFxPhF ∉+∈=γ
5) Rango y Anisotropías
Distancia
Variograma R1R2

Variograma

Más contenido relacionado

La actualidad más candente

Similar a Variograma

Más de Daniela Portillo

Último

Variograma