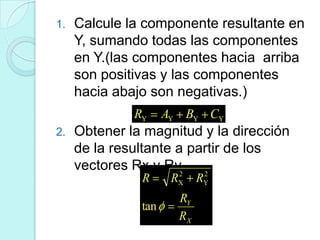
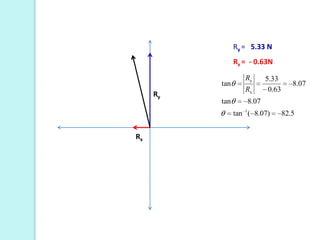
Este documento explica cómo sumar vectores utilizando el método de componentes. Primero, se descomponen los vectores en sus componentes x e y. Luego, se suman las componentes x de cada vector para obtener la componente x resultante, y se suman las componentes y para obtener la componente y resultante. Finalmente, se calcula la magnitud y dirección del vector resultante a partir de sus componentes x e y.

1. VECTORES
Amilkar Orozco
Docente de Física
Colegio Hermana Virginia Rossi

2. Componentes de un vector
Y
C (C x , C y )
Cx C cosθ
Cy C senθ
C C2 C2
x y
Cy C
Cy
0 tan
Cx
Cx X

3. Adición de Vectores por el
Método de componentes o
Analítico de este
 Pautas para la utilización
método
1. Dibuje todos los vectores a partir del
origen en un sistema de ejes
coordenados
2. Descomponga todos lo vectores en sus
componentes “Y” y “X”
3. Calcule la componente resultante en X,
sumando todas las componentes en
X.(las componentes hacia la derecha
son positivasx y las componentes hacia
R Ax Bx Cx
la izquierda son negativas.)

4. 1. Calcule la componente resultante en
Y, sumando todas las componentes
en Y.(las componentes hacia arriba
son positivas y las componentes
hacia abajo son negativas.)
RY AY BY CY
2. Obtener la magnitud y la dirección
de la resultante a partir de los
vectores Rx y Ry. 2
2
R RX RY
RY
tan
RX

5. SUMA DE VECTORES POR COMPONENTES
RECTANGULARES
B=5N
By Rx = Ax + Bx
A=3N
Rx = (2.58 N)+ (-3.21 N)
Ay
50º 30º Rx = - 0.63N
Bx Ax
Ry = Ay + By
Ry = (1.5 N) + (3.83 N)
Ry = 5.33 N
Ax = A Cos 30º = (3 N) Cos 30º = 2.58 N
Ay = A Sen 30º = 3 N Sen 30 = 1.5 N R2 = (Rx)2 + (Ry)2
Bx = -B Cos 50º = -5 N Cos 50º = - 3.21 N R2 = (-0.63N)2 + (5.33N)2
By = B Sen 50º = 5 N Sen 50º = 3.83
N R2 = 0.39 + 28.4
R2 = 28.79
R = 5.36N

6. Ry = 5.33 N
Rx = - 0.63N
Ry 5.33
tan 8.07
Rx 0.63
Ry
tan 8.07
tan 1 ( 8.07) 82.5
Rx