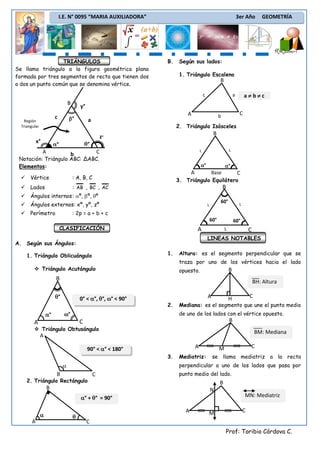
TRIANGULOS
- 1. I.E. N° 0095 “MARIA AUXILIADORA” 3er Año GEOMETRÍA TRIÁNGULOS B. Según sus lados: Se llama triángulo a la figura geométrica plana formada por tres segmentos de recta que tienen dos 1. Triángulo Escaleno B a dos un punto común que se denomina vértice. c a a≠b≠c B y° A b C c β° a Región Triangular 2. Triángulo Isósceles B z° x° θ° α° A C L L b Notación: Triángulo ABC: ∆ABC. Elementos: α° α° A Base C Vértice : A, B, C 3. Triángulo Equilátero Lados : AB , BC , AC B Ángulos internos : αº, βº, θº 60° Ángulos externos: xº, yº, zº L L Perímetro : 2p = a + b + c 60° 60° CLASIFICACIÓN A L C LINEAS NOTABLES A. Según sus Ángulos: 1. Triángulo Oblicuángulo 1. Altura: es el segmento perpendicular que se traza por uno de los vértices hacia el lado Triángulo Acutángulo opuesto. B B BH: Altura θ° 0° < α°, θ°, ω° < 90° A H C 2. Mediana: es el segmento que une el punto medio α° ω° de uno de los lados con el vértice opuesto. A C B Triángulo Obtusángulo BM: Mediana A 90° < α° < 180° A M C 3. Mediatriz: se llama mediatriz a la recta α perpendicular a uno de los lados que pasa por B C punto medio del lado. 2. Triángulo Rectángulo B B N α° + θ° = 90° MN: Mediatriz A M C α θ A C Prof: Toribio Córdova C.
- 2. I.E. N° 0095 “MARIA AUXILIADORA” 3er Año GEOMETRÍA 4. Bisectriz interior: es la bisectriz de uno de los 10. Cálculo de un ángulo externo ángulos interiores que llega del lado opuesto. B y° x° = α° + θ° θ° α α BD: Bisectriz interior y° = α° + ω° A D C α° ω° x° 5. Bisectriz exterior: es la bisectriz de uno de los ángulos exteriores que llega a la prolongación del 11. Desigualdad Triangular lado opuesto. B θ BE: Bisectriz exterior a b θ c A C E Sea: a < b < c 6. Ceviana interior: se llama así a cualquier 1. b–a<c<b+a segmento que trazado de los vértices llega al 2. c – a < b < c + a lado opuesto. B 3. c – b < a < c + b BP: Ceviana interior PROPIEDADES ADICIONALES A P C 1. Propiedad Cuadrilátero Cóncavo. 7. Ceviana exterior: se llama así a cualquier (La del Boumerang) segmento que trazado por uno de los vértices llega a la prolongación del lado opuesto. β° B x = α° + θ° + β° BQ: Ceviana exterior α° θ° x Q A C PROPIEDADES BASICAS 2. Propiedad Mariposa 8. Suma de Ángulos Internos α B x θ x + y = α° + θ° θ° α° + θ° + ω° = 180° y α° ω° 3. Propiedad Pescadito A C 9. Suma de Ángulos Externos x+y=α+θ x e2 e1 + e2 + e3 = 360° α θ e3 y e1 Prof: Toribio Córdova C.
- 3. I.E. N° 0095 “MARIA AUXILIADORA” 3er Año GEOMETRÍA 4. y° 5. Calcular “x”, si: α + θ = 60º m° a) 150º x° + y° = m° + n° b) 120º θ+3α c) 100º x° n° x° d) 20º θ-α e) 10º 5. 6. Calcular “x”; si es entero: x° a) 180º 180° + x° = α° + θ° b) 94º c) 86º x° 136° 140° d) 96º α° θ° e) 84º EJERCICIOS DE APLICACIÓN 7. Hallar los valores pares de “x”. 1. Calcular “x”. a) 4 y 6 a) 30º b) 4 y 8 b) 40º 30° c) 2 y 4 7 2 c) 50º d) 6, 7 y 8 d) 60º x° 20° e) 6 y 8 x e) 70º 8. En un triángulo ABC se traza la ceviana interior AE, sobre la cual se toma un punto D, luego se 2. Calcular “x”. traza EF perpendicular al lado AC. Hallar a) 100º m∢AEF, si m∢BAE = 15° y m∢ACB = 20°, b) 80º AD = DB = BE c) 120º 80° a) 40º b) 60º c) 80º x° d) 140º 120° d) 20º e) 10º e) 180º 9. Calcular “x”. 3. Calcular “x”. 60° a) 120º a) 50º x° b) 100º b) 100º x° c) 90º c) 180º d) 75º α° α° d) 90º 40° e) 60º α° α° e) 120º 150° 4. Calcular “x”. a) 50º 10. Calcular el mayor ángulo de un triángulo, 3x° sabiendo que uno de ellos es 40º y los otros son b) 40º c) 30º iguales. d) 20º a) 30º b) 40º c) 80º x° 2x° e) 10º d) 70º e) 50º Prof: Toribio Córdova C.
- 4. I.E. N° 0095 “MARIA AUXILIADORA” 3er Año GEOMETRÍA 11. Del gráfico: calcule “x + y”. 17. Hallar el mayor valor entero del perímetro del ∆ C a) 100º equilátero ABC. b) 90º y a) 32 B c) 110º 60° b) 30 5 40° c) 31 d) 120º x d) 29 e) 130º 6 e) 28 D A 12. Del gráfico: calcule “x”. a) 10º x 18. Del gráfico, calcule “x”. b) 20º a) 60º c) 30º 50° b) 70º 130° x 30° d) 40º c) 80º e) 50º d) 45º x θ e) 50º θ 13. Hallar “x” a) 40º 19. Del gráfico, calcular “x + y”. 100° b) 50º c) 60º x d) 70º a) 170º 45º e) 80º 60° b) 160º c) 180º x d) 190º y 14. En un triángulo escaleno de lados enteros, 2 e) 200º lados miden 2 y 3 respectivamente. Hallar el tercer lado. a) 2 b) 3 c) 4 20. Determine: “xº + yº + zº”. d) 5 e) 6 a) 100º θº θº θº b) 120º xº 15. Del gráfico: calcule ∅. a) 18º ∅ c) 150º yº b) 36º d) 180º αº c) 40º ∅ ∅ e) 360º αº d) 50º αº zº e) 45º ∅ ∅ L1 16. Del gráfico: L1 // L2 calcule la medida de “x”. a) 100º α b) 120º α c) 130º d) 140º x 60º e) 150º β L 2 β Prof: Toribio Córdova C.
