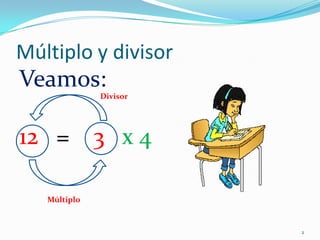
Este documento presenta los criterios de divisibilidad para determinar si un número es divisible por otros números sin necesidad de dividir. Explica que un número es divisible por 2 si su último dígito es par, por 3 si la suma de sus dígitos es divisible por 3, y por 5 si termina en 0 o 5. También cubre la divisibilidad por 7, 11, 10 y otros números mediante la multiplicación de sus dígitos de derecha a izquierda o la suma de dígitos impares menos pares.

1. CRITERIOS DE DIVISIBILIDAD Profesor: Erick Vásquez Llanos I.E.P. LATINO 2 º – Aula Virtual

2. Múltiplo y divisor Veamos: 12 = 3 x 4 2 Divisor Múltiplo

3. Múltiplo 3 N es múltiplo de a, si EXISTE un k tal que: N=a.k Ejemplo 1: a) 15 es múltiplo de 5 pues existe 3/ 15=5.3 Ejemplo 2: b) 42 es múltiplo de 7 pues existe …/ 42=7….

4. Divisor 4 a es divisor de N, si EXISTE un k tal que: N=a.k Ejemplo 1: a) 5 es divisor de 45 pues existe 9/ 45=9.5 Ejemplo 2: b) 7 es divisor de 21 pues existe…/ 21=7….

5. Criterios de divisibilidad Son reglas que nos permiten determinar si un número dado es divisible o no por otro, sin tener que efectuar la división. 5

6. Divisibilidad por 2 Un número es divisible por 2 cuando la cifra de las unidades es par. Ejemplos: 6 Observa: Todos estos números son divisibles por 2 porque la cifra de las unidades es par, pues 0, 8, 6 y 4 son pares. 750 438 56 4354

7. Divisibilidad por 3 Un número es divisible por 3 cuando la suma de todas sus cifras es múltiplo de 3. Ejemplos: 7 Observa: Todos estos números son divisibles por 3 porque al sumar sus cifras se obtiene un múltiplo de 3.

8. Divisibilidad por 5 Un número es divisible por 5 cuando la cifra de las unidades es 0 ó 5. Ejemplos: 8 Observa: Todos estos números son divisibles por 5 porque la cifra de las unidades es 0 en unos casos y 5 en otros. 750 435 255 4350

9. Divisibilidad por 7, 11, 13 9 Sea N = abcdefg, N es múltiplo de 7; 13; 11 si sus cifras al multiplicar de derecha a izquierda por: Nos da un múltiplo de7; 13; 11 respectivamente 7 - 2 -3 -1 2 3 1 4 3 -1 -4 -3 1 13 -1 1 -1 1 -1 1 11

11. Divisibilidad por 10 Un número es divisible por 10 cuando la cifra de las unidades es 0. Ejemplos: 11 Observa: Todos estos números son divisibles por 10 porque la cifra de las unidades es 0 en todos los casos. 700 430 250 4000

12. Divisibilidad por 11 Un número es divisible por 11 cuando la suma de las cifras de lugar impar, menos la suma de las cifras de lugar par, es múltiplo de 11. Ejemplo: Determinamos si 59 697 es múltiplo de 11. 7+6+5 = 18 59 697 9+9 = 18 Luego: 18 – 18 = 0 Como la diferencia obtenida es 0; y 0 es múltiplo de 11, afirmamos que 59 697 es múltiplo de 11. 12

13. FIN DE LA CLASE