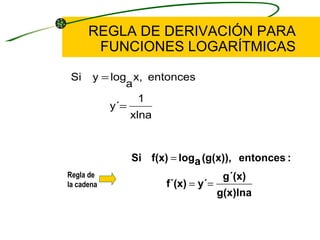
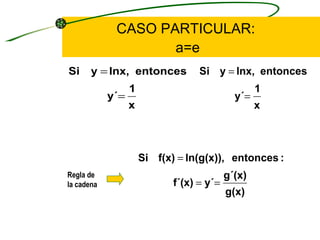
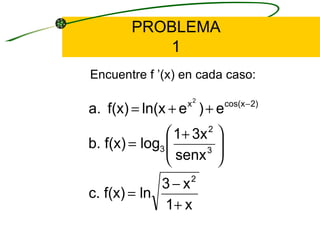
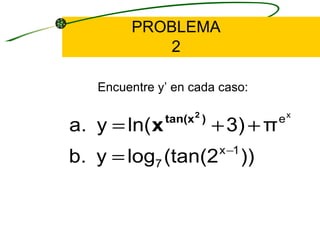
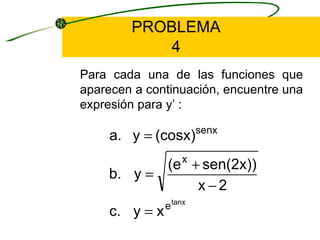
El documento describe los pasos para derivar funciones logarítmicas. Explica la regla de la cadena para funciones logarítmicas y da ejemplos de problemas de derivación de funciones que involucran logaritmos. También cubre la diferenciación logarítmica, dando los cuatro pasos para aplicar este método a ecuaciones implícitas. Finalmente, presenta más problemas de derivación de funciones logarítmicas.

1. DERIVADAS DE FUNCIONES LOGARÍTMICAS Urzua Luis

2. REGLA DE DERIVACIÓN PARA FUNCIONES LOGARÍTMICAS Regla de la cadena

3. CASO PARTICULAR: a=e Regla de la cadena

4. PROBLEMA 1 Encuentre f ’(x) en cada caso:

5. PROBLEMA 2 Encuentre y’ en cada caso:

6. PROBLEMA 3 Encuentre la ecuación de la recta tangente a la curva dada en el punto de abcisa x=1.

7. DIFERENCIACIÓN LOGARÍTMICA Es un método de derivación que se utiliza para hallar derivadas de funciones “ complicadas ” que involucren productos, cocientes y potencias…..

8. DIFERENCIACIÓN LOGARÍTMICA PASOS A SEGUIR: Sacar logaritmos a ambos lados de la ecuación dada: y=f(x) Aplicar propiedades de los logaritmos Derivar respecto de x a ambos lados de la ecuación (diferenciación implícita) Despejar y’ de la ecuación resultante 1 2 3 4

9. PROBLEMA 4 Para cada una de las funciones que aparecen a continuación, encuentre una expresión para y’ :

10. PROBLEMA 5 Derive las siguientes funciones:

11. REFLEXIÓN Cuando comprendas que la prisa es innecesaria... entonces avanzarás rápidamente! Anónimo