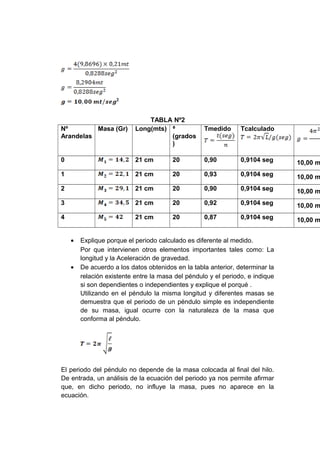
Este documento resume las actividades de un laboratorio sobre el péndulo simple. Se estudió cómo varía el periodo al cambiar el ángulo de oscilación, la masa y la longitud del péndulo. Los resultados mostraron que el periodo varía poco con ángulos pequeños, es independiente de la masa y es proporcional a la raíz cuadrada de la longitud. También se analizó cómo la velocidad aumenta con el ángulo y cómo desplazar el centro de gravedad afecta la longitud efectiva.

1. República Bolivariana de Venezuela
Universidad Fermín Toro
Escuela de Ingeniería
LABORATORIO DE FISICA 1
PRACTICA Nº4
PENDULO SIMPLE
Integrante:
Raynier Davila 21274231
Sección SAIA A

2. INTRODUCCION
Existen movimientos que se repiten a intervalos iguales de tiempo, los
cuales son llamados movimientos periódicos. Mediante el siguiente
informe se demuestra que por medio de los cálculos de datos obtenidos
empíricamente, se puede calcular cual será el resultado de la gravedad
experimental. En Física se ha idealizado un tipo de movimiento
oscilatorio, en el que se considera que sobre el sistema no existe la
acción de las fuerzas de rozamiento, es decir, no existe disipación de
energía y el movimiento se mantiene invariable, sin necesidad de
comunicarle energía exterior a este, el cual es llamado movimiento
Armónico simple.

3. Actividades de Laboratorio:
Actividad Nro. 1. Determinar el periodo y su relación con el ángulo de
oscilación, manteniendo la longitud y masa constantes.
TABLA Nº 1
(grados)ᶿ n L (mts) M (gr) T (seg)
5 10 30 cm 15 gr 17,4367 1,74367
10 10 30 cm 15 gr 13,158 1,3158
15 10 30 cm 15 gr 10,7375 1,07375
20 10 30 cm 15 gr 11,9687 1,19687
30 10 30 cm 15 gr 7,00075 0,700075
¿Cómo varia el periodo al variar el ángulo de oscilación?
El periodo de un péndulo varía con respecto a la amplitud, cuando se
trabaja con ángulos muy pequeños, el periodo varía muy poco, esto
físicamente es conocido como la ley de isocronismo.
Actividad Nro. 2. Determinar el periodo y su relación con la masa,
permaneciendo constantes el ángulo de oscilación y la longitud.

4. TABLA Nº2
Nº
Arandelas
Masa (Gr) Long(mts) ᶿ
(grados
)
Tmedido Tcalculado
0 21 cm 20 0,90 0,9104 seg 10,00 m
1 21 cm 20 0,93 0,9104 seg 10,00 m
2 21 cm 20 0,90 0,9104 seg 10,00 m
3 21 cm 20 0,92 0,9104 seg 10,00 m
4 21 cm 20 0,87 0,9104 seg 10,00 m
• Explique porque el periodo calculado es diferente al medido.
Por que intervienen otros elementos importantes tales como: La
longitud y la Aceleración de gravedad.
• De acuerdo a los datos obtenidos en la tabla anterior, determinar la
relación existente entre la masa del péndulo y el periodo, e indique
si son dependientes o independientes y explique el porqué .
Utilizando en el péndulo la misma longitud y diferentes masas se
demuestra que el periodo de un péndulo simple es independiente
de su masa, igual ocurre con la naturaleza de la masa que
conforma al péndulo.
El periodo del péndulo no depende de la masa colocada al final del hilo.
De entrada, un análisis de la ecuación del periodo ya nos permite afirmar
que, en dicho periodo, no influye la masa, pues no aparece en la
ecuación.

5. Actividad Nro. 3. Determinar el periodo y su relación con la longitud,
manteniendo la masa y el ángulo de oscilación constantes.
TABLA Nº3
Long (mts) Masa (gr) (grados)ᶿ Tmedido Tcalculado
19,4
1 Arandela
20 0,60 0,6283 seg
19,4 20 0,84 0,8885 seg
1 Arandela 20 1,08 1,0882 seg
19,4 20 1,26 1,2566 seg
1 Arandela 20 1,41 1,4049 seg
Si se miden los periodos de un mismo péndulo simple, haciendo variar
únicamente su longitud, se comprueba que, el periodo de un péndulo
simple es proporcional a la raíz cuadrada de su longitud.
Actividad Nro. 4. Calcular la rapidez del péndulo.
TABLA Nº4
(grados)ᶿ Long (mts) / v / cm / seg
5 21 cm 20
10 21 cm 28
15 21 cm 40
20 21 cm 54
30 21 cm 76
• ¿Qué pasa con la velocidad medida que aumenta el ángulo de
oscilación?
A medida que aumenta el ángulo de oscilación aumenta la velocidad, es
decir, que la velocidad del péndulo depende del ángulo de oscilación del
mismo.

6. Actividad Nro. 4. Efecto del desplazamiento del centro de gravedad en el
péndulo por variación de la masa.
La longitud real se calcula mediante la siguiente expresión:
LT= L + (valor numérico en relación al número de masas.)
0 Arandelas
LT= 21 cm + 0,7 cm = 21,07 cm
2 Arandelas
LT= 21 cm + 0,2 cm = 21, 02 cm
4 Arandelas
LT= 21 cm – 0,2 cm = 20,08 cm
POST-LABORATORIO
Se tiene un péndulo cuyo periodo de oscilación es de 5 seg.
1. Determine el valor de la gravedad en un punto del espacio donde el
periodo del péndulo aumenta ¼ del valor del periodo que tiene en
tierra.

7. CONCLUSIONES
Desarrollando la experiencia del movimiento pendular hemos podido
verificar las leyes que rigen este movimiento. Realizando nosotros
mismos las experiencias necesarias. Estas leyes que fueron establecidas
hace muchos años, aun siguen vigentes como los primeros tiempos en
que fueron escritas.