Este examen de precálculo contiene 14 secciones con varios problemas relacionados con distancias entre puntos, funciones, gráficas, ecuaciones de círculos, dominios y alcances de funciones, operaciones con funciones como suma, resta, multiplicación y división, derivadas e inversas de funciones. Los estudiantes deben mostrar su trabajo y presentar el examen antes de las 9 am del 3 de septiembre.

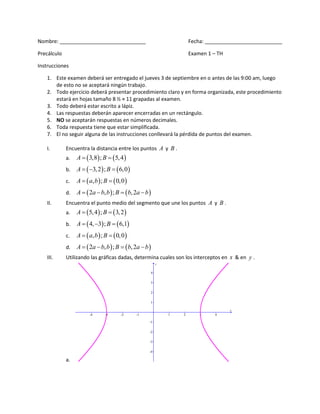
1. Nombre: ______________________________ Fecha: ___________________________
Precálculo Examen 1 – TH
Instrucciones
1. Este examen deberá ser entregado el jueves 3 de septiembre en o antes de las 9:00 am, luego
de esto no se aceptará ningún trabajo.
2. Todo ejercicio deberá presentar procedimiento claro y en forma organizada, este procedimiento
estará en hojas tamaño 8 ½ × 11 grapadas al examen.
3. Todo deberá estar escrito a lápiz.
4. Las respuestas deberán aparecer encerradas en un rectángulo.
5. NO se aceptarán respuestas en números decimales.
6. Toda respuesta tiene que estar simplificada.
7. El no seguir alguna de las instrucciones conllevará la pérdida de puntos del examen.
I. Encuentra la distancia entre los puntos A y B .
a. A   3,8 ; B   5, 4 
b. A   3, 2  ; B   6,0 
c. A   a, b  ; B   0,0 
d. A   2a  b, b  ; B   b, 2a  b 
II. Encuentra el punto medio del segmento que une los puntos A y B .
a. A   5, 4  ; B   3, 2 
b. A   4, 3 ; B   6,1
c. A   a, b  ; B   0,0 
d. A   2a  b, b  ; B   b, 2a  b 
III. Utilizando las gráficas dadas, determina cuales son los interceptos en x & en y .
y
4
3
2
1
x
-4 -3 -2 -1 1 2 3 4
-1
-2
-3
-4
a.

2. y
1
x
-π -π/2 π/2 π
-1
b.
y
9
8
7
6
5
4
3
2
1
x
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-1
-2
-3
-4
-5
-6
-7
-8
-9
c.
y
2
1
x
-3 -2 -1 1 2 3
-1
-2
d.
IV. Determina los interceptos de las siguientes funciones algebraicamente.
a. y  x  2

3. b. y  x2  9
c. 9 x 2  4 y  36
d. 4 x2  y  4
V. Encuentra el centro y el radio de los siguientes círculos, luego escribe la ecuación.
y
(0,1) (2,1)
x
a.
y
(1,2) (4,2)
x
b.
VI. Escribe la ecuación del círculo que cumple con la condición dada.
a. Centro en el origen y que contiene el punto (-2,3).
b. Centro en (1,0) y que contiene el punto (-3,2).
c. Con extremos del diámetro en (1,4) y (-3,2).
d. Con extremos del diámetro en (4,3) y (0,1).
VII. Determina el centro y el radio de los círculos con las siguientes ecuaciones.
a. x2  y 2  4x  4 y 1  0
b. x2  y 2  x  2 y  1  0

4. c. 2 x2  2 y 2  12 x  8 y  24  0
d. 2 x2  2 y 2  8x  7  0
VIII. Determina si las siguientes relaciones representan funciones, luego establece sus dominio y
alcance.
a. {(-2,5),(-1,3),(3,7),(4,12)}
b. {(0,-2),(1,3),(2,3),(3,7)}
c. {(-4,4),(-3,3),(-2,2),(-1,1),(-4,0)}
d. {(-2,16),(-1,4),(0,3),(1,4)}
IX. Encuentra los siguientes valores para cada función.
(1) f  0 (2) f 1 (3) f  1 (4) f   x  (5)  f  x  (6) f  x  1 (7) f  2x  (8) f  x  h 
a. f  x   2 x 2  x  1
x
b. f  x 
x 1
2
x2 1
c. f  x 
x4
d. f  x   x2  x
X. Encuentra el dominio de las siguientes funciones.
x2
a. f  x 
x2  1
x4
b. f  x  3
x  4x
x
c. f  x 
x4
d. f  x  x  2
XI. Para las funciones f y g , encuentra las siguientes funciones y establece el dominio de
cada una.
f
(1) f  g (2) f  g (3) f  g (4)
g
a. f  x   x  1; g  x   2 x 2
b. f  x   2 x  1; g  x   3x  2
2
c. f  x   x  1; g  x  
x
2x  3 4x
d. f  x  ; g  x 
3x  2 3x  2

5. f  x  h  f  x
XII. Encuentra ; h  0 para cada función. Asegúrate de simplificar.
h
a. f  x   3x  1
b. f  x   x2  x  4
c. f  x   x3  2
1
d. f  x 
x3
XIII. Determina f g , g f , f f y g g , para las siguientes funciones.
a. f  x  x ; g  x  x  3
2
b. f  x   3x  2; g  x   x3
1
c. f  x  ; g  x  x
x
1
d. f  x   ; g  x   x2 1
2x 1
XIV. Encuentra  g f  3 ,  f g 1 y  f f  0  , para las siguientes funciones.
a. f  x   3x  2; g  x   x 2
b. f  x   x  2 ; g  x    x2
c. f  x   x; g  x   3
d. f  x   x 2  1; g  x   x