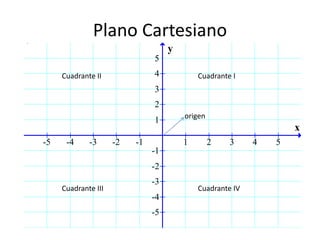
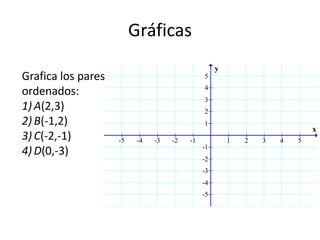
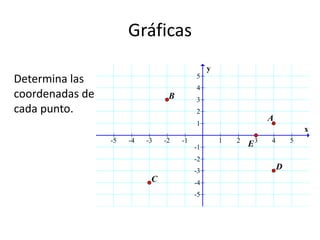
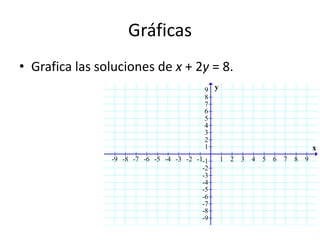
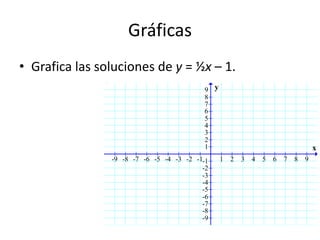
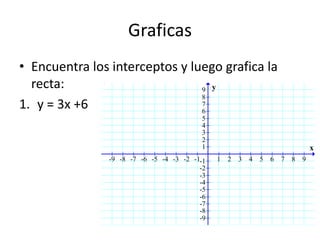
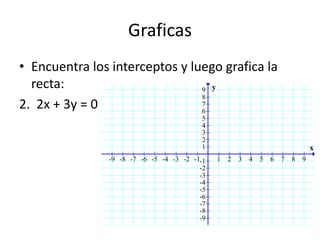
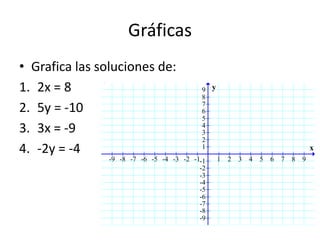
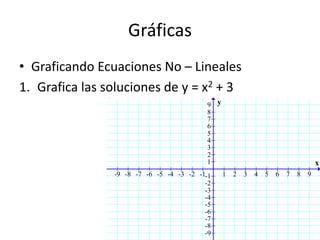
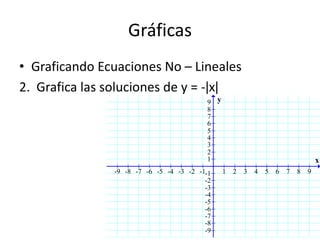
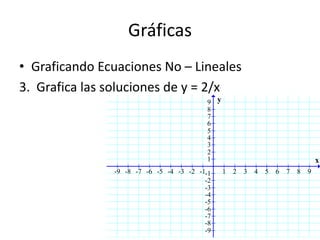
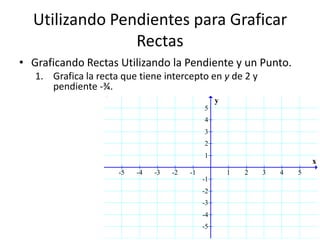
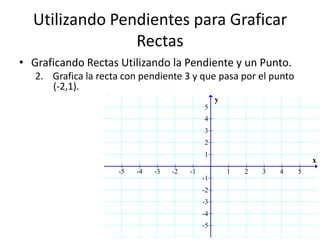
Este documento presenta información sobre gráficas y funciones lineales. Explica conceptos clave como el plano cartesiano, cómo graficar puntos y líneas, encontrar interceptos y pendientes, y escribir ecuaciones de líneas en diferentes formas estándar.

1. Gráficas y Funciones
GEMA1200

2. Plano Cartesiano
y
5
Cuadrante II 4 Cuadrante I
3
2
origen
1
x
-5 -4 -3 -2 -1 1 2 3 4 5
-1
-2
-3
Cuadrante III Cuadrante IV
-4
-5

3. Gráficas
y
Grafica los pares 5
4
ordenados:
3
1) A(2,3) 2
2) B(-1,2) 1
x
3) C(-2,-1) -5 -4 -3 -2 -1 1 2 3 4 5
-1
4) D(0,-3)
-2
-3
-4
-5

4. Gráficas
y
Determina las 5
4
coordenadas de B 3
cada punto. 2
A
1
x
-5 -4 -3 -2 -1 1 2
-1 E3 4 5
-2
-3
D
C -4
-5

5. Gráficas
• Forma Estándar de Ecuaciones Lineales
– Cualquier ecuación que pueda ser escrita de la
forma Ax + By = C es una ecuación lineal en dos
variables y la gráfica de sus soluciones es una línea
recta.
– La forma Ax + By = C es llamada la forma estándar
de la ecuación donde A, B y C son enteros, A y B
no son ambos cero y A es no negativo.

6. Gráficas
• Grafica las soluciones de x + 2y = 8.
9 y
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

7. Gráficas
• Grafica las soluciones de y = ½x – 1.
9 y
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

8. Gráficas
• Graficando Utilizando Interceptos
– Procedimiento
• Para encontrar el intercepto en x, colocamos y = 0 y
encontramos x: (x,0) es el intercepto en x.
• Para encontrar el intercepto en y, colocamos x = 0 y
encontramos y: (0,y) es el intercepto en y.

9. Graficas
• Encuentra los interceptos y luego grafica la
recta: 9 y
8
1. y = 3x +6 7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

10. Graficas
• Encuentra los interceptos y luego grafica la
recta: 9 y
8
2. 2x + 3y = 0 7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

11. Gráficas
• Graficando Rectas Horizontales y Verticales
– La gráfica de todas las soluciones de y = C es una
recta horizontal.
– La gráfica de todas las soluciones de x = C es una
recta vertical.

12. Gráficas
• Grafica las soluciones de:
1. 2x = 8 9 y
8
2. 5y = -10 7
6
5
3. 3x = -9 4
3
2
4. -2y = -4 1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

13. Gráficas
• Graficando Ecuaciones No – Lineales
1. Grafica las soluciones de y = x2 + 3
9 y
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

14. Gráficas
• Graficando Ecuaciones No – Lineales
2. Grafica las soluciones de y = -ǀxǀ
9 y
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

15. Gráficas
• Graficando Ecuaciones No – Lineales
3. Grafica las soluciones de y = 2/x
9 y
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

16. Utilizando Pendientes para Graficar
Rectas
• Definición de Pendiente
Si A  x 1 , y1  y B  x2 , y2  son dos puntos distintos
en una recta L (que no es paralela al eje de y ),
entonces la pendiente de L, denotada por m, es
y2  y1
m
x2  x1

17. Utilizando Pendientes para Graficar
Rectas
• Encuentra la pendiente de la recta que pasa a
través de los puntos dados.
1. (-3, 1), (-1, -2)
2. (-1, 5), (-1, 6)
3. (1, 1), (2, 3)
4. (3, 4), (1, 4)

18. Utilizando Pendientes para Graficar
Rectas
• Si una recta tiene pendiente positiva la gráfica
sube de izquierda a derecha.
• Si una recta tiene pendiente negativa la
gráfica baja de izquierda a derecha.
• Si una recta tiene pendiente cero la gráfica es
una recta horizontal.
• Si una recta tiene pendiente indefinida la
gráfica es una recta vertical.

19. Utilizando Pendientes para Graficar
Rectas
• Rectas Paralelas y Perpendiculares.
– Dos rectas no-verticales L1 y L2 con pendientes m1
y m2 son paralelas si y solamente si m1 = m2.
– Dos rectas L1 y L2 con pendientes m1 y m2 son
perpendiculares si y solamente si m1 = -(1/m2).

20. Utilizando Pendientes para Graficar
Rectas
• Una recta L1 tiene pendiente 2/3, determina:
a. Si la recta que pasa por los puntos (5,1) y
(8,3) es paralela o perpendicular a L1.
b. Si la recta que pasa por los puntos (-1,-4) y
(-3,-1) es paralela o perpendicular a L1.

21. Utilizando Pendientes para Graficar
Rectas
• Graficando Rectas Utilizando la Pendiente y un Punto.
1. Grafica la recta que tiene intercepto en y de 2 y
pendiente -¾.
y
5
4
3
2
1
x
-5 -4 -3 -2 -1 1 2 3 4 5
-1
-2
-3
-4
-5

22. Utilizando Pendientes para Graficar
Rectas
• Graficando Rectas Utilizando la Pendiente y un Punto.
2. Grafica la recta con pendiente 3 y que pasa por el punto
(-2,1).
y
5
4
3
2
1
x
-5 -4 -3 -2 -1 1 2 3 4 5
-1
-2
-3
-4
-5

23. Utilizando Pendientes para Graficar
Rectas
• Forma Pendiente-Intercepto de una Ecuación
Lineal
y  mx  b
intercepto en y
pendiente

24. Utilizando Pendientes para Graficar
Rectas
• Dadas las siguientes ecuaciones lineales,
encuentra la pendiente y el intercepto en y de
cada una.
1. y = 5x – 3
2. -y = ¼ x + 2
3. -3x + 2y = 7

25. Ecuaciones de Rectas
• La Forma Punto-Pendiente de una Recta
La ecuación de la recta que pasa a través de
los puntos  x1 , y1  y  x2 , y2  está dada por
y  y1  m  x  x1 
y2  y1
donde m  y  x2  x1  .
x2  x1

26. Ecuaciones de Rectas
• Encontrando una ecuación dados dos puntos.
1. Encuentra, escribe en forma estándar y grafica la
ecuación de la recta que pasa por los puntos
(5,2) y (6,4).
2. Encuentra, escribe en forma estándar y grafica la
ecuación de la recta que pasa por los puntos
(3,1) y (4,3).

27. Ecuaciones de Rectas
• Encontrando una ecuación dado un punto y la
pendiente.
1. Encuentra, escribe en forma estándar y grafica la
ecuación de la recta con pendiente m = -2 que
pasa por el punto (3, 5).
2. Encuentra, escribe en forma estándar y grafica la
ecuación de la recta con pendiente m = -3 que
pasa por el punto (1, 2).

28. Ecuaciones de Rectas
• Encontrando una ecuación dada la pendiente
y el intercepto en y.
1. Encuentra la forma pendiente-intercepto y
grafica la ecuación de la recta con pendiente 5 e
intercepto en y = 3.
2. Encuentra la forma pendiente-intercepto y
grafica la ecuación de la recta con pendiente 3 e
intercepto en y = 2.

29. Ecuaciones de Rectas
• Encontrando la ecuación de una recta que pasa a través de
un punto dado y paralela o perpendicular a una recta dada.
1. Encuentra la ecuación de la recta que pasa a través del punto
(6, 1) y es:
a) Paralela a la recta y – 3x = 1. Escribe la ecuación en forma
pendiente-intercepto.
b) Perpendicular a la recta y – 3x = 1. Escribe la ecuación en forma
pendiente-intercepto.
2. Encuentra la ecuación de la recta que pasa a través del punto
(4, 3) y es:
a) Paralela a la recta y + 2x = 7. Escribe la ecuación en forma
pendiente-intercepto.
b) Perpendicular a la recta y + 2x = 7. Escribe la ecuación en forma
pendiente-intercepto.