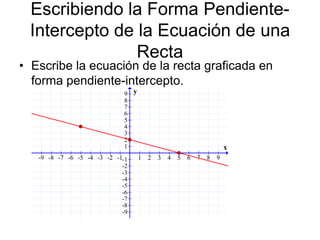
Este documento presenta información sobre cómo escribir funciones lineales en forma pendiente-intercepto y punto-pendiente. Explica cómo calcular la pendiente de una recta dados dos puntos y cómo escribir ecuaciones de rectas en diferentes formas. También cubre conceptos de rectas paralelas y perpendiculares y cómo escribir ecuaciones de rectas paralelas y perpendiculares. El documento concluye con una asignación de ejercicios relacionados con estos temas.

1. Sección 2 – 4
Escribiendo Funciones Lineales
Matemática Avanzada
Undécimo grado

2. Warm Up
• Escribe cada función en forma pendiente
– intercepto.
1) 4x + y = 8
2) -y = 3x
3) 2y = 10 – 6x
• Determina si la recta es vertical u
horizontal.
4) x = ¾
5) y = 0

3. Objetivos
• Utilizar la forma pendiente-intercepto y
punto-pendiente para escribir funciones
lineales.
• Escribir funciones lineales para resolver
problemas.

4. Escribiendo la Forma Pendiente-
Intercepto de la Ecuación de una
Recta
• Escribe la ecuación de la recta graficada en
forma pendiente-intercepto.
9 y
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

5. Escribiendo la Forma Pendiente-
Intercepto de la Ecuación de una
Recta
• Escribe la ecuación de la recta graficada en
forma pendiente-intercepto.
9 y
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1-1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

6. Fórmula de Pendiente
La fórmula de la pendiente de la recta que contiene los puntos (x1, y1)
y (x2, y2) es:
y2  y1
m
x2  x1

7. Encontrando la Pendiente de una
Recta dados Dos o más Puntos
• Encuentra la pendiente de cada recta.
1. La recta que pasa por los puntos (3, -2) y
(-1, 2).
2. La recta que pasa por los puntos (-1, 1) y
(2, -5)

8. Encontrando la Pendiente de una
Recta dados Dos o más Puntos
• Encuentra la pendiente de cada recta.
3. 1
x 2 5 8 11
y 1 6 11 16
4. 1
x 4 8 12 16
y 2 5 8 11

9. Encontrando la Pendiente de una
Recta dados Dos o más Puntos
• Encuentra la pendiente de cada recta.
y
1. De la recta mostrada. 4
2
x
-4 -2 2 4
-2
-4
y
2. De la recta mostrada. 4
2
x
-4 -2 2 4
-2
-4

10. Forma Punto-Pendiente
• La ecuación de una recta con pendiente m y el
punto (x1, y1) es:
y  y1  m  x  x1 

11. Escribiendo Ecuaciones de Rectas
• Escribe la ecuación de la recta que contiene los
puntos en la tabla en la forma pendiente-
intercepto.
x -3 -1 1 3
y 1.5 1 0.5 0

12. Escribiendo Ecuaciones de Rectas
• Escribe la ecuación de la recta que contiene los
puntos en la tabla en la forma pendiente-
intercepto.
x -8 -4 4 8
y -5 -3.5 -0.5 1

13. Escribiendo Ecuaciones de Rectas
• Escribe la ecuación de cada recta en
forma pendiente-intercepto.
1. Con pendiente -5 y que pasa por (1, 3).
2. Que pasa por los puntos (-2, -3) y (2, 5).

14. Rectas Paralelas y
Perpendiculares
• Rectas paralelas
– Si ambas pendientes están definidas, las pendientes
de rectas paralelas son iguales.
– Las pendientes de rectas verticales paralelas están
indefinidas.
• Rectas perpendiculares
– Si ambas pendientes están definidas, las pendientes
de rectas perpendiculares son recíprocos opuestos.
– Una recta vertical y una recta horizontal son
perpendiculares.

15. Escribiendo Ecuaciones de Rectas
Paralelas y Perpendiculares
• Escribe la ecuación de cada recta en
forma pendiente-intercepto.
1. Paralela a y = 1.5x + 6 y que pasa por (4, 5).
2. Perpendicular a y = -¾x + 2 y que pasa por
(6, -4).
3. Paralela a y = 1.8x + 3 y que pasa por (5, 2).
4. Perpendicular a y = -3/2 x – 1 y que pasa
por (9, -2).

16. Asignación
• Páginas 121 – 122, ejercicios 14, 16, 18 –
20, 30, 36.