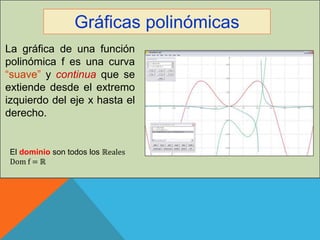
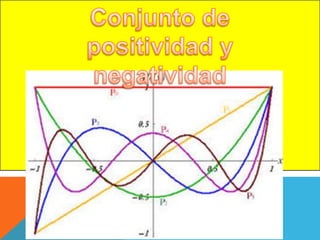
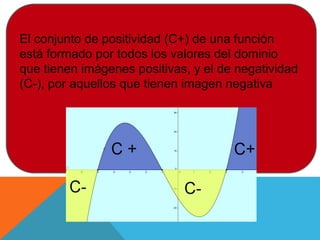
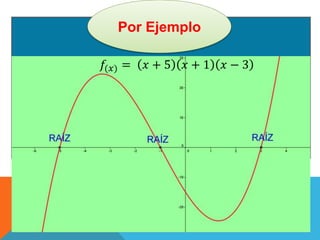
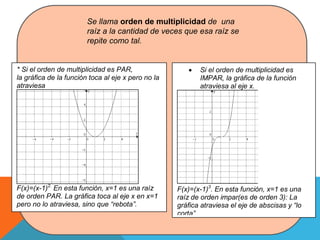
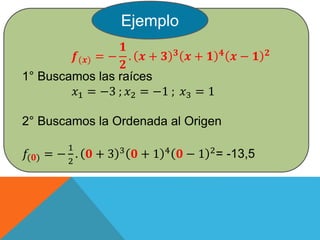
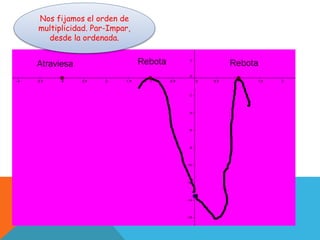
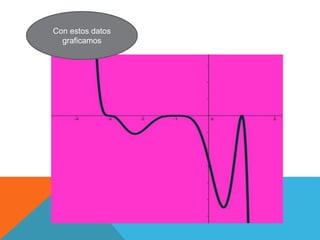
El documento discute el uso de funciones polinómicas en el mundo real, como en el lanzamiento de cohetes. Explica que las funciones polinómicas se utilizan en física, finanzas, medicina y más. Luego describe las características gráficas de funciones polinómicas como su dominio, conjunto de positividad, raíces y orden de multiplicidad de las raíces.

1. Díaz Miguel Gustavo

2. Todos sabemos que las matemáticas son utilizadas en todas partes,
pero a veces nos preguntamos si el pensamiento de orden superior de
matemáticas se utiliza en el mundo real? ¿que creen?, las funciones
polinómicas son importantes, especialmente para los científicos en el
lanzamiento de cohetes o satélites, los polinomios se utilizan en la
física, las finanzas, la medicina, la biología, la agricultura y muchos
más. La evaluación de las funciones polinómicas así como la solución
de sus ecuaciones conduce a un teorema básico de álgebra llamado
teorema fundamental del álgebra.

3. Gráficas polinómicas
La gráfica de una función
polinómica f es una curva
“suave” y continua que se
extiende desde el extremo
izquierdo del eje x hasta el
derecho.
El dominio son todos los ℝeales
Dom f = ℝ

5. El conjunto de positividad (C+) de una función
está formado por todos los valores del dominio
que tienen imágenes positivas, y el de negatividad
(C-), por aquellos que tienen imagen negativa

6. Las raíces o ceros son los valores del dominio
cuya imagen es cero. En el grafico son los
puntos donde intersecta la grafica con el eje x.
Si la formula de una función está de forma
factorizada, entonces podemos identificar
de forma sencilla las raíces.

7. Por Ejemplo
𝑓(𝑥) = 𝑥 + 5 𝑥 + 1 𝑥 − 3

8. Se llama orden de multiplicidad de una
raíz a la cantidad de veces que esa raíz se
repite como tal.
* Si el orden de multiplicidad es PAR,
la gráfica de la función toca al eje x pero no la
atraviesa
F(x)=(x-1)2.
En esta función, x=1 es una raíz
de orden PAR. La gráfica toca al eje x en x=1
pero no lo atraviesa, sino que “rebota”.
 Si el orden de multiplicidad es
IMPAR, la gráfica de la función
atraviesa al eje x.
F(x)=(x-1)3
. En esta función, x=1 es una
raíz de orden impar(es de orden 3): La
gráfica atraviesa el eje de abscisas y “lo
corta”

9. Ejemplo
𝒇(𝒙) = −
𝟏
𝟐
. 𝒙 + 𝟑 𝟑 𝒙 + 𝟏 𝟒 𝒙 − 𝟏 𝟐
1° Buscamos las raíces
𝑥1 = −3 ; 𝑥2 = −1 ; 𝑥3 = 1
2° Buscamos la Ordenada al Origen
𝑓(𝟎) = −
1
2
. 𝟎 + 3 3
𝟎 + 1 4
𝟎 − 1 2
= -13,5

10. Marcamos los puntos en
los ejes

11. Nos fijamos el orden de
multiplicidad. Par-Impar,
desde la ordenada.

12. Con estos datos
graficamos

13. Profesor:
Díaz Miguel
Gustavo