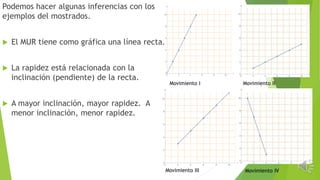
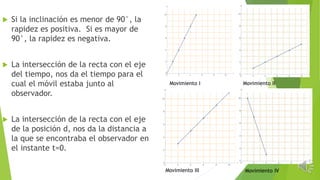
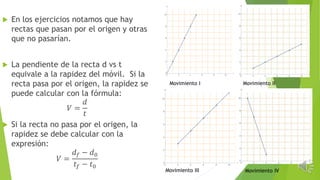
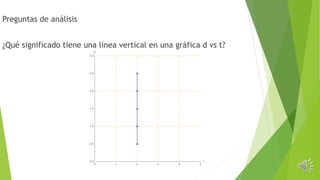
El documento explica el movimiento uniforme rectilíneo (MUR), donde la trayectoria es lineal y la rapidez es constante en el tiempo. Se analizan ejemplos y gráficos que muestran cómo la velocidad y el desplazamiento se relacionan, así como cómo calcular la rapidez a partir de diferentes datos. Además, se discute la relación entre la inclinación de la recta en gráficas de distancia versus tiempo y la rapidez del móvil.

1. Movimiento Uniforme
Rectilíneo (MUR)
www.sistemastzolkin.com

2. Características del MUR
 La trayectoria es en línea recta.
 La rapidez es constante en todo tiempo.
Por lo tanto, la
velocidad se mantiene
constante en el
tiempo.

3. Observaciones:
 Si el vector Velocidad es constante en el
tiempo, esto significa que el módulo (rapidez),
dirección y sentido de la velocidad no cambian
en el tiempo.
 La rapidez es constante en todo tiempo.
 Como el vector Velocidad tiene la misma
dirección y sentido que el vector
desplazamiento, al tener el vector Velocidad al
transcurrir el tiempo la misma dirección y
sentido, el vector desplazamiento tampoco
cambia su dirección y sentido. Por lo tanto, la
trayectoria debe ser una línea recta.

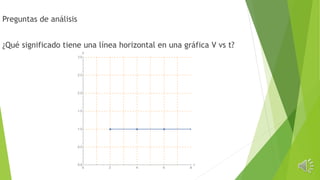
4. ¿Qué significa que la rapidez es
constante en el tiempo?
 Que un móvil recorre distancias iguales en tiempos
iguales.
Para apreciar mejor esa idea, observe la siguiente tabla que
muestra la posición de un móvil contra el tiempo.
t [s] d [m]
0 0
1 2
2 4
3 6
4 8
5 10
 Se puede inferir, que el móvil se mueve con rapidez V=2 [m/s]
Movimiento I

5. Aprovechando la gráfica del
movimiento de este cuerpo,
responda lo siguiente:
 ¿Cuál será la posición del
cuerpo en t=7 [s]?
 ¿Para qué valor de
tiempo, se habrá
alcanzado la posición 15
[m]?
 ¿Cuánto habrá recorrido
el cuerpo entre 5 y 14
[s]?

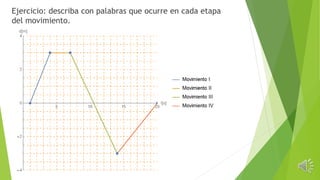
6. Veamos otro ejemplo.
 Un observador tomó los siguientes datos de un cuerpo en
movimiento:
t[m] d[m]
2 1
4 2
6 3
8 4
10 5
Utilicemos esta información para responder las siguientes preguntas
 ¿El cuerpo lleva una rapidez constante?
 ¿De cuánto es su rapidez?
 ¿Qué significado tiene esta rapidez?
 ¿En qué momento pasó el cuerpo junto al observador?
 Observe la gráfica de este movimiento. ¿En qué se parece al del movimiento anterior?
Movimiento II

7. Veamos otro ejemplo.
Un observador tomó los siguientes datos del movimiento de un cuerpo, olvidando
escribir algunos.
t[m] d[m]
2 3
4 5
6 7
8 9
10 11
Responda las siguientes preguntas.
 ¿El cuerpo lleva rapidez constante?
 ¿De cuánto es su rapidez?
 ¿Qué significado tiene esta rapidez?
 ¿En qué momento paso el cuerpo junto al observador?
 ¿A qué distancia del observador se encontraba en el
instante de tiempo t=0 [s]?
Movimiento III

8. Veamos un último ejemplo. Se tienen los siguientes datos tomados
por un observador del movimiento de un cuerpo.
t[s] d[m]
1 10
2 7
3 4
4 1
Responda las siguientes preguntas.
 ¿El cuerpo lleva rapidez constante?
 ¿De cuánto es su rapidez?
 ¿Qué significado tiene esta rapidez?
 ¿En qué momento paso el cuerpo junto al observador?
 ¿A qué distancia del observador se encontraba en el
instante de tiempo t=0 [s]?
Movimiento IV

9. Podemos hacer algunas inferencias con los
ejemplos del mostrados.
 El MUR tiene como gráfica una línea recta.
 La rapidez está relacionada con la
inclinación (pendiente) de la recta.
 A mayor inclinación, mayor rapidez. A
menor inclinación, menor rapidez.
Movimiento I Movimiento II
Movimiento III Movimiento IV

10.  Si la inclinación es menor de 90°, la
rapidez es positiva. Si es mayor de
90°, la rapidez es negativa.
 La intersección de la recta con el eje
del tiempo, nos da el tiempo para el
cual el móvil estaba junto al
observador.
 La intersección de la recta con el eje
de la posición d, nos da la distancia a
la que se encontraba el observador en
el instante t=0.
Movimiento I Movimiento II
Movimiento III Movimiento IV

11.  En los ejercicios notamos que hay
rectas que pasan por el origen y otras
que no pasarían.
 La pendiente de la recta d vs t
equivale a la rapidez del móvil. Si la
recta pasa por el origen, la rapidez se
puede calcular con la fórmula:
𝑉 =
𝑑
𝑡
 Si la recta no pasa por el origen, la
rapidez se debe calcular con la
expresión:
𝑉 =
𝑑 𝑓 − 𝑑0
𝑡𝑓 − 𝑡0
Movimiento I Movimiento II
Movimiento III Movimiento IV

12. En los ejercicios anteriores, la velocidad se mantiene constante
durante todo el tiempo que transcurre el movimiento. De tal
forma, que si graficáramos la velocidad (rapidez) contra el
tiempo, tendríamos lo siguiente.

13. Las cuatro rectas son horizontales. Y además, si obtuviéramos el
área bajo cada una, ésta equivale a la distancia recorrida total
(df-d0)

14. Preguntas de análisis
¿Qué significado tiene una línea horizontal en una gráfica d vs t?

15. Preguntas de análisis
¿Qué significado tiene una línea vertical en una gráfica d vs t?

16. Preguntas de análisis
¿Qué significado tiene una línea horizontal en una gráfica V vs t?

17. Ejercicio: describa con palabras que ocurre en cada etapa
del movimiento.