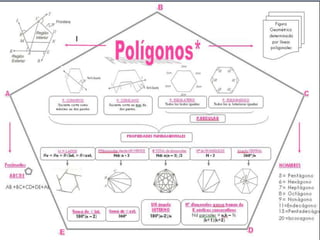
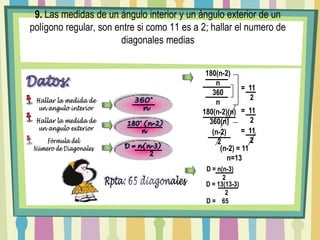
El documento presenta 10 problemas relacionados con polígonos regulares y el cálculo de sus diagonales. Los problemas incluyen calcular la suma de diagonales de dos polígonos dados sus lados, encontrar el polígono donde el número de diagonales es cuádruple del número de lados, y calcular el número de diagonales de polígonos regulares dados otros datos como la suma de sus ángulos interiores.

1. Problemas Propuestos POLIGONOSExpositora: LIC.PATRICIA PÉREZ GARCÍA

3. 1.En un polígono regular la suma de sus medidas de ángulos interiores excede en 360º a la suma de las medidas de los ángulos exteriores, además el numero de lados de un segundo polígono excede en dos al numero de lados del primer polígono. Encontrar la suma de los números de diagonales de los polígonosDatos:ResoluciónPolígono 1S < i = 360º + S < ex180º ( n – 2 ) = 360º + 360º180º ( n – 2 ) = 720n – 2 = 4Fórmula para Hallar la Suma de angulos interioes180º ( n – 2)n = 6Polígono 2Excede en dos al número de lados del primero.n=6+ 2 = 8

4. Datos:Polígono 1 n = 6Polígono 2 n = 8Nd =n(n-3) 2Fórmula para Hallar elNúmero de DiagonalesPolígono 1Polígono 1Nd = 6 ( 6 - 3) 2 Nd = 8 ( 8 - 3) 2 Nd = 6 (3) 2 Nd = 8 (5) 2 Nd = 9 Nd = 20 Rpta: 9 + 20 = 29 diagonales

5. 2. ¿En qué polígono se cumple que el numero de diagonales es el cuádruple del numero de lados?Nd =n(n-3) 2Datos:Resoluciónn ( n - 3) = 4n 2 Polígono Nd = 4n n - 3 = 4.2 Fórmula para Hallar elNúmero de Diagonales n = 8 + 3 n = 11Rpta: Endecágono

6. 3.Hallar el número total de diagonales que se pueden trazar en un polígono de 18 lados?Nd =n (n-3) 2Datos:ResoluciónNd = 18 ( 18 - 3) 2 Polígono 18 ladosNd = 18 ( 15) 2 Fórmula para Hallar elNúmero de DiagonalesNd = 9 ( 15)Nd = 135Rpta: 135 diagonales

7. 4.Halla el número de diagonales de un polígono regular cuyos ángulos interiores sumas 1620Nd =n(n-3) 2Datos:Resolución180º ( n – 2 ) = 1620Polígono Regular 180 n - 360 = 1620 S < i = 1620180 n = 1620 + 360180 n = 1980Fórmula para Hallar la Suma de angulos interioes180º ( n – 2) n = 11Fórmula para Hallar elNúmero de Diagonales44Nd = 11 ( 8) 2 Rpta: 144 diagonales=

8. 5.¿Cuántas diagonales se podrán trazar desde 3 vértices consecutivos de un icosàgono?Nd =n.k – ½ (k+1) (k+2)Datos:ResoluciónPolígono Nd de un Icosàgono (20 lados)Nd = 20.3 – ½ ( 3 + 1) (3+2)Nd = 60 – ½ ( 4) (5)Fórmula para Hallar elNúmero de Diagonales ParcialesNd = 60 – ½ 20Nd = 60 – 10Rpta: 50diagonales

9. 6. ¿Cuál es el polígono regular en el que si se aumentara en 52 el numero de diagonales, el numero de lados aumentara en 8?Datos:Polígono 1D = Dn = nPolígono 2D = D+52n = n+8Resolución(n+8)(n+8-3) - n (n-3) = 52122D - D = 52(n+8) (n+5) – n + 3n = 5221122 n +5n+8n+40-n +3n = 52 . 22216n + 40 = 104216n = 642n = 4D = n(n-3) 2Fórmula para Hallar elNúmero de DiagonalesRpta: Cuadrado

10. 7. La suma de ángulos internos de un polígono no convexo es 1080°. Hallar el número de diagonalesDatos:Resolución1080°180(n-2) = 1080n-2 = 1080 180n = 6+2n = 8D = n(n-3) 2Fórmula delNúmero de DiagonalesFórmula Suma de los Angulos interiores 180° (n-2) D = n(n-3) 2D = 8(8-3) 2D = 8(5) 2D = 20Rpta: 20 diagonales

11. 8. Tengo un polígono convexo de 25 lados. Calcule el numero total de diagonales trazadas desde todos los vérticesDatos:Resoluciónn = 25 D = n(n-3) 2 D = 25(25-3) 2 D = 25(22) 2 D = 25(11)D = 275Fórmula delNúmero de DiagonalesD = n(n-3) 2Rpta: 275 diagonales

12. 9. Las medidas de un ángulo interior y un ángulo exterior de un polígono regular, son entre si como 11 es a 2; hallar el numero de diagonales medias180(n-2)n 360n= 11 2Datos:Hallar la medida deun angulo interior360° n= 11 2180(n-2)(n)360(n)Hallar la medida deun angulo exterior 180° (n-2) n = 11 2(n-2)2Fórmula delNúmero de Diagonales(n-2) = 11n=13D = n(n-3) 2 D = n(n-3) 2Rpta: 65 diagonales D = 13(13-3) 2 D = 65

13. 10. Calcular el numero de lados de aquel polígono en el cual al disminuir dos lados su numero de diagonales disminuye en 19Datos:Polígono 1D = Dn = nPolígono 2D = D-19n = n-2Resoluciónn (n-3) – (n-2)(n-2-3) = 1922n -3n – (n-2)(n-5) = 38D - D = 19212n -3n – (n-5n-2n+10) = 3822n -3n-n+5n+2n-10 = 38224n = 48n = 12D = n(n-3) 2Fórmula delNúmero de DiagonalesRpta: 12 lados

14. GRACIAS!!! =D