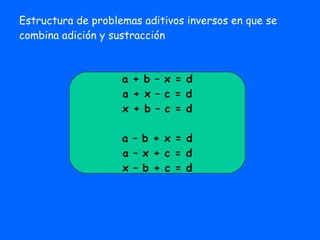
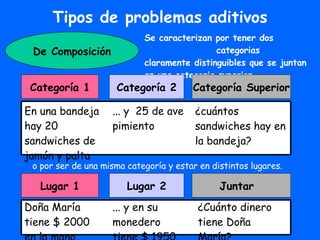
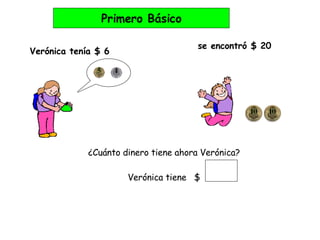
Este documento describe los tipos de problemas aditivos que se abordan en educación básica. Explica que los problemas aditivos involucran sumas y restas, y pueden ser simples o combinados. También describe tres tipos de problemas aditivos - de cambio, composición y comparación - asociados a diferentes acciones matemáticas. Finalmente, resume cómo se enseñan los problemas aditivos a lo largo de la educación básica, comenzando con los simples en primero básico y avanzando a los combinados.

1. CAMPO DE PROBLEMAS ADITIVOS Profesor Juan Vergara Cuevas MINEDUC Nivel de Educación Básica Equipo de Matemática

2. Situación Problemática Modelos Matemáticos u Operaciones Esquemas Trabajo con el Modelo: Cálculos Resultado del Cálculo Procedimientos o Algoritmos Respuesta al Problema ¿Cómo abordarla y resolverla? ¿Cómo enseñar a resolverla?

3. CARACTERIZACIÓN DE LOS PROBLEMAS ADITIVO S Un problema pertenece al campo aditivo cuando la operación que se realiza par a resolverlo es una adición o u na sustracción En la panera hay 6 hallullas y 5 marraquetas. ¿Cuánto pan hay en la panera? 6 + 5 = Laura tenía $ 300 y compró un helado de $ 100. ¿Con cuánto dinero quedó? 300 – 100 =

4. Una Operación Según el números de operaciones que se realice para resolver un problema , estos pueden ser simples o combinados Más de una Operación

5. Problemas aditivos simples Un problema aditivo es simple cuando para resolverlo se efectúa solo una adición o una sustracción Problema Simple de Adición Andrés toma el ascensor en el noveno piso de un edificio y sube 8 pisos. ¿A qué piso llegó? 9 + 8 = Problema Simple de Sustracción Paola tiene $ 5.000 y se compró una polera de $ 3.000 ¿Con cuánto dinero quedó Paola? 5.000 – 3.000 = Estos problemas tienen dos datos.

6. Problemas aditivos combinados Un problema aditivo es combinado cuando para resolverlo se efectúa más de una adi ción , más de una sustracción o combinaciones de ellas.

7. Estos problemas tienen más de dos datos. Doña Rosa tiene 40 gallinas, 20 patos y 8 pavos. ¿cuántas aves tiene doña Rosa? 40 + 20 + 8 = Daniel tenía 48 bolitas.Jugó y perdió 12 bolitas.Volvió a jugar y perdió otras 8 bolitas. ¿Con cuántas bolitas quedó Daniel? 48 – 12 – 8 = Claudia tenía $ 150, su papá le dio $ 300 y en la escuela se compró un jugo de $ 250. ¿Con cuánta plata quedó Claudia? 150 + 300 – 250 =

8. Según el lugar que ocupa la incógnita, los problemas aditivos pueden ser directos e inversos Si a, b y c representan los datos y x la incógnita, su estructura es: Simples Combinados a + b = x a + b + c = x a – b = x a – b – c = x a + b – c = x a – b + c = x Si a, b, c y d representan los datos y x la incógnita, su estructura es: Simples Combinados a + x = c a + b + x = d x + b = c a + x + c = d x + b + c = d a – x = c a – b – x = d x – b = c a – x – c = d x – b – c = d

9. Estructura de problemas aditivos inversos en que se combina adición y sustracción a + b – x = d a + x – c = d x + b – c = d a – b + x = d a – x + c = d x – b + c = d

10. Claudio tenía 15 bolitas , jugó y ganó . A hora tiene 24. ¿Cuántas bolitas ganó Claudio? 15 + x = 24 Pamela tenía $ 85 y se encontró $ 100. ¿Cuánto dinero tiene ahora Pamela? 85 + 100 = x Ambos son Problemas Aditivos Simples El de Pamela es Directo El de Claudio es Inverso

11. Julio tenía 45 bolitas. Primero ganó 11 y luego perdió 10. ¿Cuántas bolitas tiene ahora Julio? 45 +11 – 10 = X Nena tiene $ 300, su padre le dio $ 500 Camino a la escuela se compró un helado y quedó con $ 600. ¿Cuánto le costó el helado? 300 + 500 – X = 600 Ambos son Problemas Aditivos Combinados El de Julio es Directo El de Nena es Inverso

12. Tipos de problemas aditivos De Cambio Se caracterizan por tener : Una Situación Inicial Una acción de cambio Y una Situación Final Carla tenía $ 850, su madre le dio $ 1.000. ¿Cuánto dinero tiene ahora Carla ? Simón tenía 68 bolitas, jugó y perdió 15. ¿Con cuántas bolitas quedó Simón? María estaba en el 8° piso de un edificio. Subió 16 pisos. ¿A qué piso llegó María?

13. Este tipo de problemas está asociado a las acciones de “ agregar-quitar”y “avanzar-retroceder” mencionadas en los Programas de Estudio. Otras acciones asociadas a problemas de cambio son “ ahorrar-gastar”, “ganar-perder”, “ subir-bajar”, “vender-comprar”.

14. Tipos de problemas aditivos De Composición Se caracterizan por tener dos categorias claramente distinguibles que se juntan en una categoria superior Categoría 1 Categoría 2 Categoría Superior En una bandeja hay 20 sandwiches de jamón y palta ... y 25 de ave pimiento ¿cuántos sandwiches hay en la bandeja? Lugar 1 Lugar 2 Juntar Doña María tiene $ 2000 en la mano, ... y en su monedero tiene $ 1950. ¿Cuánto dinero tiene Doña María? o por ser de una misma categoría y estar en distintos lugares.

15. Este tipo de problemas está asociado a las acciones de “ juntar-separar” mencionadas en los Programas de Estudio.

16. Tipos de problemas aditivos De Comparación Se caracterizan porque se comparan dos cantidades o medidas del mismo tipo. Cantidad o Medida 1 Cantidad o Medida 2 Diferencia Sebastián pesa 48 kilos . Rayen pesa 36 kilos. ¿Cuántos kilos menos que Sebastián pesa Rayen? Cantidad o Medida 1 Diferencia Cantidad o Medida 2 Ramón tiene 254 corderos. Manuel tiene 46 corderos más que Ramón. ¿Cuántos corderos tiene Manuel?

17. Este tipo de problemas está asociado a las acciones de “ comparar por diferencia” mencionadas en los Programas de Estudio.

18. Primero Básico ¿Cuánto dinero tiene ahora Verónica? Verónica tiene $ se encontró $ 20 Verónica tenía $ 6

19. Segundo Básico Claudia tiene $ 58 Jorge tiene $ 50 ¿Quién tiene más dinero? ¿Cuánto más? Leonel y Nelson fueron juntos a pescar al río. Leonel pescó 20 truchas. Nelson pescó 5 truchas más que Leonel. ¿Cuántas truchas pescó Nelson?

20. Tercero Básico Cuatro amigos juegan a las bolitas . Julio tenía 50 bolitas. En el primer juego ganó 12 bolitas y en e l segundo juego ganó 15. ¿Cuántas bolitas tiene ahora Julio? Andrés tenía 58 bolitas. En el primer juego perdió 9 y en el segundo perdió 13. ¿Cuántas bolitas tiene ahora Andrés? Marco llegó con 45 bolitas. Primero ganó 11 y después perdió 10. Ahora, ¿cuántas bolitas tiene Marco? Cristián tenía 60 bolitas. Primero perdió 16 y después ganó 10. ¿Cuántas bolitas tiene ahora Cristián?

21. Ante la dificultad generalizada de los niños para determinar la operación matemática con la que se resuelve un problema... Se requiere poner a su disposición, herramientas que les permitan analizar/estudiar el enunciado de un problema: Los Esquemas Los esquemas deben ser funcionales para la persona que estudia el problema. No deben ser una imposición; si una niña o un niño resuelve el problema directamente del enunciado, hacer un esquema sería una pérdida de tiempo. Sería una tarea inútil para ese niño o esa niña. Los esquemas pueden ser de distinto tipo, pero deben representar las relaciones entre datos e incógnita. No debemos olvidar que las niñas y los niños tienen que manejar procedimientos de cálculo eficaces.

22. María tiene 156 aves, de las cuales 50 son gallinas, 45 son patos y las demás son pavos. ¿Cuántos pavos tiene María? 156 50 45 X 50 + 45 + X = 156 95 Cuarto Básico

23. En NB1 se estudian los Problemas Aditivos Simples, Directos e Inversos Primero Básico Semestre 1 Asociados a las acciones de “ agregar-quitar” y “ juntar-separar”. Semestre 2 Asociados a las acciones de “ agregar-quitar”, “ juntar-separar” y “ avanzar- retroceder”. Segundo Básico Semestre 3 Asociados a las acciones de “ comparar por diferencia”. Semestre 4 Asociados a todas las acciones estudiadas anteriormente.

24. En NB2 se estudian los Problemas Aditivos Combinados, Directos e Inversos Tercero Básico Cuarto Básico Semestre 1 Sencillos y directos, asociados a todas las acciones estudiadas, y combinaciones de ellas. Semestre 2 Sencillos, directos e inversos, asociados a todas las acciones estudiadas, y combinaciones de ellas. Semestre 3 Complejos y directos, asociados a todas las acciones estudiadas, y combinaciones de ellas. Semestre 4 Complejos, directos e inversos, asociados a todas las acciones estudiadas, y combinaciones de ellas .