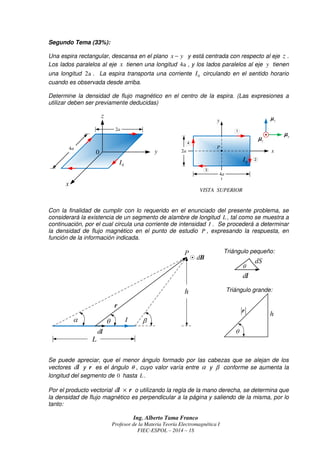
Este documento presenta tres problemas de teoría electromagnética resueltos por un profesor. El primer problema determina la función de permitividad y capacitancia de un cable coaxial con dieléctrico no homogéneo. El segundo calcula la densidad de flujo magnético en el centro de una espira rectangular. El tercero encuentra las corrientes de magnetización y flujos magnéticos producidos por un cilindro magnetizado.