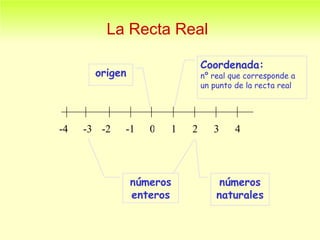
Este documento describe conceptos básicos de los números reales y conjuntos. Introduce la recta real, números naturales, enteros y orden numérico. Explica la notación de intervalos en la recta real como (a,b), [a,b], (-∞,b), etc. También define conjuntos de números reales como uniones e intersecciones y el valor absoluto de un número.

1. La Recta Real origen números naturales Coordenada: nº real que corresponde a un punto de la recta real -1 0 1 2 3 4 -2 -3 -4 números enteros

2. Orden y desigualdades a , b  I R a es menor que b si b-a es positivo Este orden se denota por la desigualdad a  b Análogamente mayor que  menor o igual que  mayor o igual que  Recordar que cuando se multiplica por un número negativo se invierte la desigualdad x  3  -4 x  -12

3. Conjuntos Un conjunto es una colección de elementos Conjunto de los números Reales I R Conjunto de los números reales positivos  x  I R : x  0  Conjunto de los números reales no negativos  x  I R : x  0  Unión de dos conjuntos: A  B es el conjunto de elementos de A, de B o de ambos Intersección de dos conjuntos: A  B es el conjunto de elementos de A y de B El conjunto de todos los x que satisfacen una cierta condición  x : condición sobre x  Notación

4. Intervalos de la recta real (a, b) =  x : a  x  b  Intervalo abierto extremos [a, b] =  x : a  x  b  Intervalo cerrado

5. Intervalos acotados Intervalo acotado abierto (a, b)  x : a  x  b  ( ) a b x Intervalo acotado cerrado [a, b]  x : a  x  b  [ ] a b x Intervalos acotados [ a, b)  x : a  x  b  [ ) a b x ni abiertos ni cerrados (a, b]  x : a  x  b  ( ] a b x Notación de intervalos Notación de conjuntos Gráfica

6. Intervalos no acotados Intervalos no acotados (-  , b)  x : x  b  ) b x abiertos (a,  )  x : x  a  ( a x Notación de intervalos Notación de conjuntos Gráfica Intervalos no acotados (-  , b]  x : x  b  ] b x cerrados [a,  )  x : x  a  [ a x Recta real (-  ,  )  x : x  I R  x a b

7. Valor absoluto Si a es un número real, el valor absoluto de a es Ejemplo: a = -4 | a | = | -4 | = - (-4) = 4 | a | = a si a  0 -a si a  0