MATEMÁTICA APLICADA PARA INGENIERÍA

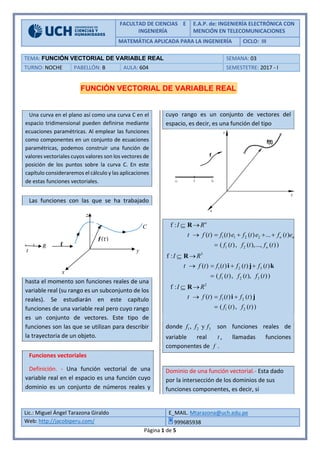
1. FACULTAD DE CIENCIAS E
INGENIERÍA
E.A.P. de: INGENIERÍA ELECTRÓNICA CON
MENCIÓN EN TELECOMUNICACIONES
MATEMÁTICA APLICADA PARA LA INGENIERÍA CICLO: III
Lic.: Miguel Ángel Tarazona Giraldo E_MAIL. Mtarazona@uch.edu.pe
Web: http://jacobiperu.com/ 999685938
Página 1 de 5
TEMA: FUNCIÓN VECTORIAL DE VARIABLE REAL SEMANA: 03
TURNO: NOCHE PABELLÓN: B AULA: 604 SEMESTETRE: 2017 - I
FUNCIÓN VECTORIAL DE VARIABLE REAL
Una curva en el plano así como una curva C en el
espacio tridimensional pueden definirse mediante
ecuaciones paramétricas. Al emplear las funciones
como componentes en un conjunto de ecuaciones
paramétricas, podemos construir una función de
valores vectoriales cuyos valores son los vectores de
posición de los puntos sobre la curva C. En este
capítulo consideraremos el cálculo y las aplicaciones
de estas funciones vectoriales.
Las funciones con las que se ha trabajado
hasta el momento son funciones reales de una
variable real (su rango es un subconjunto de los
reales). Se estudiarán en este capítulo
funciones de una variable real pero cuyo rango
es un conjunto de vectores. Este tipo de
funciones son las que se utilizan para describir
la trayectoria de un objeto.
Funciones vectoriales
Definición. - Una función vectorial de una
variable real en el espacio es una función cuyo
dominio es un conjunto de números reales y
cuyo rango es un conjunto de vectores del
espacio, es decir, es una función del tipo
1 1 2 2
1 2
f :
( ) ( ) ( ) ... ( )
( ( ), ( ),..., ( ))
n
n n
n
I R
t f t f t e f t e f t e
f t f t f t
 
    

R
3
1 2 3
1 2 3
f :
( ) ( ) ( ) ( )
( ( ), ( ), ( ))
I R
t f t f t f t f t
f t f t f t
 
   

R
i j k
2
1 2
1 2
f :
( ) ( ) ( )
( ( ), ( ))
I R
t f t f t f t
f t f t
 
  

R
i j
donde 1 2 3, yf f f son funciones reales de
variable real t , llamadas funciones
componentes de f .
Dominio de una función vectorial.- Esta dado
por la intersección de los dominios de sus
funciones componentes, es decir, si
•
f
t
𝒇(𝑡)
C
t
z
y
x
R

2. FACULTAD DE CIENCIAS E
INGENIERÍA
E.A.P. de: INGENIERÍA ELECTRÓNICA CON
MENCIÓN EN TELECOMUNICACIONES
MATEMÁTICA APLICADA PARA LA INGENIERÍA CICLO: III
Lic.: Miguel Ángel Tarazona Giraldo E_MAIL. Mtarazona@uch.edu.pe
Web: http://jacobiperu.com/ 999685938
Página 2 de 5
1 2 3( ) ( ( ), ( ), ( ))f t f t f t f t entonces
1 2 3(f) ( ) (f ) (f )I Dom Dom f Dom Dom 
Ejemplo: Si  2
( ) 1 , ,f t t t ln t  el
dominio de f será  0/  ttI R
Rango o imagen de f.- sea f: I → Rn
una
función vectorial tal que
1 2( ) ( ( ), ( ),..., ( ))nf t f t f t f t
, definimos
Im(f) = {(f1(t), f2(t), f3(t), … , fn(t))/ tεI},
donde Im(f) = f(I)
Traza de f.- El conjunto imagen f(I) ⊂ ℝ3
se
denomina la traza de f.
Nota: Si la función vectorial f describe el
movimiento de una partícula, el vector
1 2 3( ) ( ( ), ( ), ( ))f t f t f t f t señala su posición
en el instante t , en estos casos t representa el
variable tiempo.
Ejemplo 1:
3
: / ( ) (2 3 ) 2 ( 1 )f f t t t t      R R i j k
Ejemplo 2:
3 2
: / ( ) ( , , 3 )f f t t sent cos t R R
Ejemplo 3:
Grafique la curva trazada por la función
vectorial
f(t) = 2costi + 2sentj + 3k
Solución
Parametrizando {
x = 2cost
y = 2sent
z = 3
Un punto de la curva ya sobre la curva:
x2
+ y2
= 4, sin embargo, como la
coordenada z de cualquier punto tiene el valor
constante z = 3
Ejemplo 4:
Determine la función vectorial que describe la
curva C de intersección del plano y = 2x y el
paraboloide: z = 9 − x2
− y2
.
Solución
Parametrizando la curva C de intersección
dejando x = t se deduce que y = 2t y
z = 9 − t2
− (2t)2
= 9 − 5t2
de acuerdo a
las ecuaciones paramétricas.
{
x = t
y = 2t
z = 9 − 5t2
− ∞ < t < +∞
función vectorial que describe el trazo del
paraboloide en el plano la función vectorial
que describe el trazo del paraboloide en el
plano
y = 2x está dada por:
f⃗(t) = ti + 2tj + (9 − 5t2
)k

3. FACULTAD DE CIENCIAS E
INGENIERÍA
E.A.P. de: INGENIERÍA ELECTRÓNICA CON
MENCIÓN EN TELECOMUNICACIONES
MATEMÁTICA APLICADA PARA LA INGENIERÍA CICLO: III
Lic.: Miguel Ángel Tarazona Giraldo E_MAIL. Mtarazona@uch.edu.pe
Web: http://jacobiperu.com/ 999685938
Página 3 de 5
Ejemplos
• Un campo vectorial para el movimiento del
aire en la tierra asociará a cada punto en la
superficie de la tierra un vector con la velocidad
y la dirección del viento en ese punto. Esto se
puede dibujar usando flechas para representar
el viento; la longitud (magnitud) de la flecha será
una indicación de la velocidad del viento. Un
"Alta" en la función usual de la presión
barométrica actuaría, así como una fuente
(flechas saliendo), y un "Baja" será un sumidero
(flechas que entran), puesto que el aire tiende a
moverse desde las áreas de alta presión a las
áreas de presión baja.
• Un campo de velocidad de un líquido móvil.
En este caso, un vector de velocidad se asocia a
cada punto en el líquido. En un túnel de viento,
las líneas de campo se pueden revelar usando
humo.
• Campos magnéticos. Las líneas de campo se
pueden revelar usando pequeñas limaduras de
hierro.
• Las ecuaciones de Maxwell permiten que
utilicemos un conjunto dado de condiciones
iniciales para deducir, para cada punto en el
espacio euclidiano, una magnitud y una
dirección para la fuerza experimentada por una
partícula de prueba cargada en ese punto; el
campo vectorial que resulta es el campo
electromagnético.
Ejercicios
01. Determine el dominio de la función vectorial
definida por
a. f⃗(t) = (ln(t) , t2
, √1 − t )
b. f⃗(t) = (√t ,
1
√t−1
, ln(4 − t2
))
c. f⃗(t) = (t ,
1
√t−1
, ln(4 − t))
d. f⃗(t) = (√t − 3 , √t + 3 , t3
)
e. f⃗(t) = (t2
− 4 ,
1
√t−1
, ln(
4−t
√t2−9
))
f. f⃗(t) = (t ,
1
√t2+5t−20
, ln(t2
− 5t + 6))
g. f⃗(t) = (
1
t+2
,
8
√9−t2
, ln(t20
+ 5))
2. Hallar el Dominio de las siguientes
Funciones Vectoriales de Variable Escalar:
) ( ) t
a f t e i Sent j 
1 3
) ( )
5 1
b f t i j
t t
 
 
d) 3
) ( ) ( 4, 7, )c f t t t t  
 ) ( ) (2 8), (7 )e f t Ln t Ln t  

4. FACULTAD DE CIENCIAS E
INGENIERÍA
E.A.P. de: INGENIERÍA ELECTRÓNICA CON
MENCIÓN EN TELECOMUNICACIONES
MATEMÁTICA APLICADA PARA LA INGENIERÍA CICLO: III
Lic.: Miguel Ángel Tarazona Giraldo E_MAIL. Mtarazona@uch.edu.pe
Web: http://jacobiperu.com/ 999685938
Página 4 de 5
3. Hallar el Dominio de las siguientes
funciones vectoriales de variable Escalar:
) ( ) t
a f t e i sent j 
1 3
) ( )
5 1
b f t i j
t t
 
 
5
) ( ) 5 5t
c f t t i j t k  
3
) ( ) ( 4, 7, )d f t t t t  
 ) ( ) (2 8), (7 )e f t Ln t Ln t  
𝑓) 𝑓⃗(𝑡) = (𝑙𝑛(𝑡 + 1) , √𝑡2 + 2𝑡 − 8)
g) 𝑓⃗(𝑡) = (
𝑡2
𝑡+2
, 2𝑡3
,
2𝑡
𝑡+1
)
j) 𝑓⃗(𝑡) = (
1
𝑡2 , 0, 𝑙𝑛(𝑡 + 1))
k) 𝑓⃗(𝑡) = (
1
𝑡2+1
, 𝑙𝑛(𝑡2
− 1),
2𝑡
𝑡−1
)
l) 𝑓⃗(𝑡) = (𝑙𝑛(𝑡 − 1) , √𝑡2 − 2𝑡 − 3)
ll) 𝑓⃗(𝑡) = (𝑙𝑛(
𝑡−5
𝑡−2
, √𝑡2 − 9, 𝑡2
− 5)
m) 𝑓⃗(𝑡) = (√ 𝑡, 𝑙𝑛 (
𝑡2−9
𝑡2−36
) , 𝑡2
)
n) 𝑓⃗(𝑡) = (√9 − 𝑡2, √𝑡2 − 1, 𝑙𝑛𝑡)
04. 𝑓⃗(𝑡) = (𝑡, 3𝑡), 𝑡 ∈ 𝑅, se expresa también
con las ecuaciones paramétricas x = t, y = 3t.
La imagen o la trayectoria de f es una recta en el
plano R2
.
05. f⃗(t) = (cost, sent), t ∈ [0, 2π]. En este
caso, la trayectoria de f es la circunferencia
centrada en (0, 0) de radio 1?
06. Describa la curva en el espacio que definen
las siguientes funciones vectoriales:
a) f⃗(t) = (1 − t, 2 + 4t, 3 + 2t), t ∈ R
b) f⃗(t) = (sent, 3, cost), t ∈ R
c) f⃗(t) = (2cost, 2sent, t), t ∈ R
Las ecuaciones paramétricas de la curva 𝐶 son:
𝑥 = 2𝑐𝑜𝑠𝑡, 𝑦 = 2𝑠𝑒𝑛𝑡, 𝑧 = 𝑡, Al eliminar el
parámetro t de las primeras dos ecuaciones
2 2 2 2 2
(2cost) (2sent) 2x y   
Observamos que un punto sobre la curva yace en
el cilindro circular 2 2 2
2x y  Como advertimos en
la FIGURA y la tabla adjunta a la misma, cuando
aumenta el valor de t, la curva se enrolla hacia arriba
en una espiral cilíndrica o una hélice circular.

5. FACULTAD DE CIENCIAS E
INGENIERÍA
E.A.P. de: INGENIERÍA ELECTRÓNICA CON
MENCIÓN EN TELECOMUNICACIONES
MATEMÁTICA APLICADA PARA LA INGENIERÍA CICLO: III
Lic.: Miguel Ángel Tarazona Giraldo E_MAIL. Mtarazona@uch.edu.pe
Web: http://jacobiperu.com/ 999685938
Página 5 de 5
07. Sea f⃗: I ⊆ R ⟶ R3
, tal que f⃗(t) = (acost, 3,
bsent, t), t ∈ R esta curva es llamada hélice.
Note que {
x = acost
y = bsent
z = t
⟹ {
x2
= a2
cos2
t
y2
= b2
sen2
t
z = t
⟹
x2
a2 +
y2
b2 = 1
Se puede observar como la traza que hace la
superficie x = acosz al cilindro
x2
a2
+
y2
b2
= 1
08. Determine el domino de la función vectorial
definida por f⃗(t) = (ln(t) ; t2
; √1 − t)
09.- Un jugador de béisbol lanza una pelota con
un ángulo de 45° con respecto a la horizontal, a
una distancia de 75 metros si la pelota es
capturada al mismo nivel de lanzamiento,
determinar la rapidez inicial de lanzamiento.
10.- Un proyectil es disparado a una altura de 10
metros con una velocidad inicial de 1500m/s y
con un ángulo de elevación de 30°. Determinar:
a) la velocidad, en cualquier instante
b) la altura máxima.
c) el alcance del proyectil.
d) la rapidez con la que el proyectil choca con
el suelo.
Bibliografías
Dennis G. Zill. Cálculo con Geometría Analítica
Eduardo Espinoza Ramos. Análisis Matemático
III
G. Fuller y D. Tarwater. Geometría Analítica
Johnson, Glenn, Norton y García. Explorando la
matemática. Tomo II. New York. McGraw-Hill,
1967.
Leithold, Louis. “Cálculo con Geometría
Analítica”, Harla, sexta edición, 1992.
Referencias
https://analisisfigempa.wikispaces.com/Integral+
Doble
www.jacobiperu.com
http://usach.maximi89.cl/descargas.php
https://es.wikipedia.org/wiki/H%C3%A9lice_(geo
metr%C3%ADa)