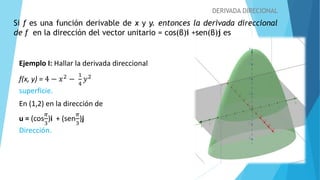
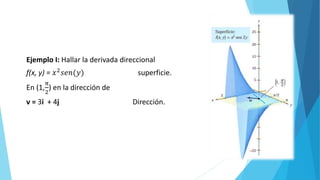
La derivada direccional de una función f(x,y) en la dirección del vector unitario u = cos(β)i + sen(β)j es igual a fx(x,y)cos(β) + fy(x,y)sen(β). Esto se puede calcular evaluando las derivadas parciales fx y fy en el punto y dirigiendo u. También es igual al producto interno entre el gradiente de f y u. El documento presenta dos ejemplos de cálculo de derivadas direccionales aplicando estas propiedades.

1. DERIVADA
DIRECIONAL

2. Si f es una función derivable de x y y. entonces la derivada
direccional de f en la dirección del vector unitario = cos(β)i
+sen(β)j es:
Propiedad 1: Duf(x,y) = fx(x,y)cos(β) + fy(x,y)sen(β)
Propiedad 2: Duf(x,y) = f(x,y)•ῡ

3. DERIVADA DIRECIONAL
Si f es una función derivable de x y y. entonces la derivada direccional
de f en la dirección del vector unitario = cos(β)i +sen(β)j es
Ejemplo I: Hallar la derivada direccional
f(x, y) = 4 − 𝑥2 −
1
4
𝑦2
superficie.
En (1,2) en la dirección de
u = (cos
𝜋
3
)i + (sen
𝜋
3
)j
Dirección.

4. Solución Como fx y fy son continuos, f es derivable, y se puede aplicar la
“propiedad 1”
Duf(x,y) = fx(x,y)cos(β) + fy(x,y)sen(β)
= (-2x)cosβ + (-
y
2
)senβ
Evaluado en β =
π
3
, X = 1 y Y = 2 se obtiene
Duf(1,2) = (-2)
1
2
+ (-1)
3
2
Duf(1,2) = -1 -
3
2

5. Ejemplo I: Hallar la derivada direccional
f(x, y) = 𝑥2 𝑠𝑒𝑛(𝑦) superficie.
En (1,
π
2
) en la dirección de
v = 3i + 4j Dirección.

6. Solución Como fx y fy son continuos, fes derivable, y se puede aplicar
la “propiedad 1”
Se comienza por calcular el vector unitario en la dirección v.
u =
𝒗
‖𝒗‖
=
𝟑
𝟓
i -
𝟒
𝟓
j = cos βi+ senβj
Usando el vector unitario, se tiene
Duf(x,y) = 2xsen(2y) cos β +2x 2 2cos(2y)senβ
Duf(1,
π
2
) = 2sen(π)
𝟑
𝟓
+2cos(π)
𝟒
𝟓
Duf(1,
π
2
) =
8
5