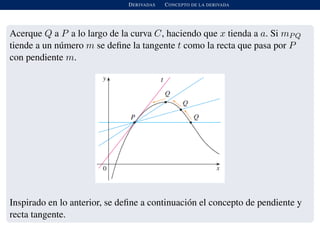
1) El documento introduce el concepto de derivada y tangente a una curva. 2) Explica cómo calcular la pendiente de la tangente como un límite y define la derivada como este límite. 3) Proporciona ejemplos del cálculo de derivadas para funciones como polinomios y raíces cuadradas.

2. DERIVADAS
Cristian Camilo Penagos Torres
Departamento de Matem´aticas, f´ısica y Estad´ıstica
Universidad de La Sabana

3. DERIVADAS CONCEPTO DE LA DERIVADA
Aqu´ı se desarrollar´an las reglas de la derivaci´on sin tener que pasar
directamente por la defici´on formal de la derivada. Estas reglas permiten
calcular con facilidad las derivadas de funciones polinomiales y
exponenciales, entre otras.

4. DERIVADAS CONCEPTO DE LA DERIVADA
Sea C una curva dada por la ecuaci´on y = f(x). Se desea hallar la tangente a la curva C en el
punto P(a, f(a)), entonces considere un punto cercano Q(x, f(x)). La pendiente de la recta
secante que pasa por los puntos P y Q esta dada por:
mP Q =
f(x) − f(a)
x − a
FIGURA: Recta secante que une dos puntos

5. DERIVADAS CONCEPTO DE LA DERIVADA
Acerque Q a P a lo largo de la curva C, haciendo que x tienda a a. Si mPQ
tiende a un n´umero m se define la tangente t como la recta que pasa por P
con pendiente m.
Inspirado en lo anterior, se define a continuaci´on el concepto de pendiente y
recta tangente.

6. DERIVADAS CONCEPTO DE LA DERIVADA
DEFINICI ´ON
La pendiente de la curva y = f(x) en el punto P(a, f(a)) es el n´umero
m = l´ım
h→0
f(a + h) − f(a)
h
siempre que el l´ımite exista. La recta tangente (o simplemente la tangente) a
la curva P es la recta que pasa por P y tiene dicha pendiente.

7. DERIVADAS CONCEPTO DE LA DERIVADA
EJEMPLO
Encuentre la pendiente de la recta tangente a la curva dada por f(x) = x2 en
el punto (1, 1)
l´ım
h→0
f(1 + h) − f(1)
h
= l´ım
h→0
(1 + h)2 − 12
h
= l´ım
h→0
1 + 2h + h2 − 1
h
= l´ım
h→0
2h + h2
h
= l´ım
h→0
h(h + 2)
h
= l´ım
h→0
(h + 2)
= 2
As´ı la pendiente de la tangente en el punto es 2.
Ver: https://ggbm.at/yzyxfzak

8. DERIVADAS CONCEPTO DE LA DERIVADA
DEFINICI ´ON
La derivada de la funci´on f en el punto x = a, denotada por
f (a) es
f (a) = l´ım
h→0
f(a + h) − f(a)
h
siempre que el l´ımite exista.

9. DERIVADAS CONCEPTO DE LA DERIVADA
EJEMPLO
Determine f (1), si f(x) =
√
x.
f (1) = l´ım
h→0
f(1 + h) − f(1)
h
= l´ım
h→0
√
1 + h −
√
1
h
= l´ım
h→0
√
1 + h −
√
1
h
·
√
1 + h +
√
1
√
1 + h +
√
1
= l´ım
h→0
1 + h − 1
h(
√
1 + h +
√
1)
= l´ım
h→0
h
h(
√
1 + h +
√
1)
= l´ım
h→0
1
√
1 + h +
√
1
= l´ım
h→0
1
√
1 + 0 +
√
1
=
1
2

10. DERIVADAS CONCEPTO DE LA DERIVADA
INTERPRETACION DE LA DERIVADA
Las siguientes son interpretaciones para el l´ımite del cociente de diferencias,
l´ım
h→0
f(a + h) − f(a)
h
1. La pendiente de la gr´afica de y = f(x) en x = a
2. La pendiente de la tangente a la curva y = f(x) en x = a
3. La tasa de cambio de f(x) respecto a x en x = a
4. La derivada f (a) en el punto

11. DERIVADAS CONCEPTO DE LA DERIVADA
DEFINICI ´ON
La derivada de la funci´on f(x) respecto a la variable x es la
funci´on f cuyo valor en x es
f (x) = l´ım
h→0
f(x + h) − f(x)
h
siempre que el l´ımite exista.

12. DERIVADAS CONCEPTO DE LA DERIVADA
EJEMPLO
Determine f (x), si f(x) =
√
x.
f (x) = l´ım
h→0
f(x + h) − f(x)
h
= l´ım
h→0
√
x + h −
√
x
h
= l´ım
h→0
√
x + h −
√
x
h
·
√
x + h +
√
x
√
x + h +
√
x
= l´ım
h→0
x + h − x
h(
√
x + h +
√
x)
= l´ım
h→0
1
√
x + h +
√
x
=
1
2
√
x
As´ı f (x) = 1
2
√
x
.

13. DERIVADAS NOTACI ´ON
NOTACI ´ON DE LA DERIVADA
Para denotar la derivada de una funci´on y = f(x), donde x es
la variable independiente mientras que y la variable
dependiente podemos utilizar las siguientes alternativas:
f (x) = y =
dy
dx
=
df
dx
=
d
dx
f(x) = D(f)(x) = Dxf(x)
Para indicar la derivada de f en un n´umero espec´ıfico x = a, se utiliza la
siguiente notaci´on:
f (a) =
dy
dx x=a
=
df
dx x=a
=
d
dx
f(x)
x=a

14. DERIVADAS REGLAS DE DERIVACI ´OM
REGLAS DE DERIVACI ´ON
Si f y g son funciones derivables, entonces:
1.
d
dx
(c) = 0, c es una constante
2.
d
dx
(xn
) = nxn−1
, n ∈ R
3.
d
dx
(cf(x)) = c
d
dx
f(x), c es una constante
4.
d
dx
(f(x) ± g(x)) =
d
dx
f(x) ±
d
dx
g(x)
5.
d
dx
(ex
) = ex
6.
d
dx
[f(x)g(x)] = g(x)
d
dx
[f(x)] + f(x)
d
dx
[g(x)]
7.
d
dx
f(x)
g(x)
=
g(x) d
dx [f(x)] − f(x) d
dx [g(x)]
g2(x)

15. DERIVADAS REGLAS DE DERIVACI ´OM
EJEMPLO: APLICACI ´ON REGLA DEL PRODUCTO
Encuentre la derivada de f(x) = (3x − 2x2
)(5 + 4x)
f (x) = (5 + 4x)
d
dx
[3x − x2
] + (3x − 2x2
)
d
dx
[5 + 4x]
= (5 + 4x)(3 − 4x) + (3x − 2x2
) · 4
= (15 − 8x − 16x2
) + (12x − 8x2
)
= −24x2
+ 4x + 15

16. DERIVADAS REGLAS DE DERIVACI ´OM
EJEMPLO: APLICACI ´ON REGLA DEL COCIENTE
Encuentre la derivada de g(x) =
5x − 2
x2 + 1
g (x) =
(x2 + 1) d
dx [5x − 2] − (5x − 2) d
dx [x2 + 1]
(x2 + 1)2
=
(x2 + 1)(5) − (5x − 2)(2x)
(x2 + 1)2
=
(5x2 + 5) − (10x2 − 4x)
(x2 + 1)2
=
−5x2 + 4x + 5
(x2 + 1)2