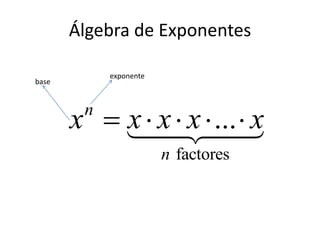
El documento introduce conceptos básicos de álgebra como expresiones, términos, propiedades distributivas, multiplicación, factorización, combinación de términos semejantes, y remoción de paréntesis. También cubre exponentes incluyendo reglas de productos, cocientes y potencias de exponentes, y notación científica como una forma de escribir números grandes y pequeños.

1. Introducción al Álgebra
GEMA1000

2. Introducción al Álgebra
• Una expresión es una colección de números y
letras conectados por operaciones.
– Ejemplos: xy2, x + y, 3x2 – 2y + 9
• Los términos en una expresión son las partes que
son sumadas o restadas.
– La expresión xy2 tiene un término (es un monomio)
– La expresión x + y tiene dos términos (es un binomio)
– La expresión 3x2 – 2y + 9 tiene tres términos (es un
trinomio)

3. Introducción al Álgebra
• La Propiedad Distributiva
 
 
Para cualquier número real , y ,a b c
a b c ab ac
a b c ab ac
  
  

4. Introducción al Álgebra
• Multiplica.
1. 2(x + 2y)
2. 5(3x – 4y)
3. -3(x – 2y + z)
4. 3(a + 5b)
5. 6(4a – 5b)
6. -2(a – 3b + c)

5. Introducción al Álgebra
• Factorizar
– Factorizar una expresión es encontrar una expresión
equivalente que es un producto.
• Factoriza
1. 3x – 6y
2. ax + ay – az
3. 10x – 20y – 30z
4. 5a – 15b
5. ab + ac – ad
6. 6a – 12b + 18c

6. Introducción al Álgebra
• Combinando Términos Semejantes
• Simplifica
1. 7x – 2x
2. 3x + 5y – x + 4y
3. 6a – 2a
4. 5a + 7b – a + 2b

7. Introducción al Álgebra
• Removiendo Paréntesis
• Simplifica
1. (3a + 5b) – (a + 2b)
2. (5a + 2b) – (6a – 3b)
3. (4a + 5b) – (a + 3b)
4. (6a + 5b) – (8a – 2b)
5. -(-2x + 5y) – 6x
6. -(-a2 – 3b) + a

8. Álgebra de Exponentes
factores
...n
n
x x x x x    
base
exponente

9. Álgebra de Exponentes
• Exponente Cero
• Exponente Negativo
0
1, 0x x 
1
, 0n
n
x x
x

 

10. Álgebra de Exponentes
• Escribe los siguientes como una fracción y
simplifica.
1. 6-2
2. 4-3
3. 5-2
4. 3-3

11. Álgebra de Exponentes
• Escribe los siguientes utilizando exponentes
negativos
1.
2.
3.
4.
4
1
5
5
1
7
4
1
7
5
1
6

12. Álgebra de Exponentes
• Regla de Productos de Exponentes
• Multiplica y simplifica.
1. 26 ∙ 22
2. x3 ∙ x4
3. 43 ∙ 4-5
4. y2 ∙ y-3
5. a-5 ∙ a5
, 0m n m n
x x x x
  

13. Álgebra de Exponentes
• Regla de Cociente de Exponentes
• Divide y simplifica.
, 0
m
m n
n
x
x x
x

 
3
2
6
1.
6
5
2.
x
x
2
2
3.
y
y


3
4
4.
z
z



14. Álgebra de Exponentes
• Regla de Potencia de Exponentes
• Simplifica.
1. (23)2
2. (x-2)6
3. (y4)-5
4. (z-2)-3
 
nm m n
x x 


15. Álgebra de Exponentes
• Regla de Potencias de Productos de
Exponentes
• Simplifica.
1. (x2y-2)3
2. (x-2y3)3
3. (x-2y3)-2
     
k k km n m n mk nk
x y x y x y 

16. Notación Científica
• Un número en notación científica es escrito
como
10 , donde, 1 10 y es un enteron
M M n  

17. Notación Científica
• Para escribir un número en notación científica
(M x 10n)
1. Mover el punto decimal en el número dado de tal
manera que solo haya un dígito a la izquierda de
este. El número resultante es M.
2. Cuenta cuantos lugares tuviste que mover el punto
decimal en el paso 1. Si el punto decimal fue movido
a la izquierda entonces n es positivo; si el punto
decimal fue movido a la derecha entonces n es
negativo.
3. Escribe M x 10n

18. Notación Científica
• Escribiendo un número en notación científica.
1. La distancia aproximada al Sol es 93,000,000
millas y el largo de onda de la luz ultravioleta es
0.000035 centímetros. Escribe ambas cantidades
en notación científica.
2. La distancia a la Luna es aproximadamente
239,000 millas y su masa es 0.0123456 veces la
de la Tierra. Escribe ambas cantidades en
notación científica.

19. Notación Científica
• Escribiendo un número en notación estándar.
1. Un jumbo jet pesa 7.75 x 105 libras, mientras
que una araña casera pesa 2.2 x 10-4 libras.
Escribe ambas cantidades en notación estándar.
2. El Concorde pesa 4.08 x 105 libras y un grillo
pesa 3.125 x 10-4 libras. Escribe ambas
cantidades en notación estándar.

20. Notación Científica
• Multiplicando números en notación científica.
1. Multiplica las partes decimales primero y escribe
el resultado en notación científica.
2. Multiplica las potencias de 10.
3. La respuesta, la cual debe estar simplificada, es
el producto del paso 1 y 2.

21. Notación Científica
• Multiplica.
1. (5 x 103) x (8.1 x 104)
2. (3.2 x 103) x (4 x 104)
3. (6 x 103) x (2.2 x 104)
4. (4.1 x 103) x (3 x 104)

22. Notación Científica
• Dividiendo números en notación científica.
1. (1.24 x 10-2) ÷ (3.1 x 10-3)
2. (2.52 x 10-2) ÷ (4.2 x 10-3)

23. Notación Científica
• Dividiendo números en notación científica.
19
18
8
5
1.02 10
1.
5.1 10
2.8 10
2.
1.4 10





24. Resolviendo Ecuaciones Lineales
• Principios para resolver ecuaciones
La ecuación es equivalente aa b
a c b c
a c b c
a c b c
a c b c
a b
c c

  
  
  
  
