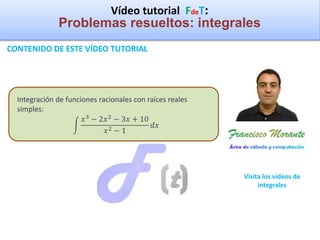
El vídeo tutorial aborda la resolución de integrales de funciones racionales, destacando el proceso de dividir polinomios y calcular integrales de forma práctica. Se examina el caso específico donde las raíces del denominador son reales simples, haciendo énfasis en la descomposición en fracciones simples y el cálculo de las integrales resultantes. Al final, se presenta un ejemplo concreto que ilustra todo el proceso desde la división hasta la obtención del resultado de la integral.

1. Vídeo tutorial FdeT:
Problemas resueltos: integrales
CONTENIDO DE ESTE VÍDEO TUTORIAL
Visita los vídeos de
integrales
Integración de funciones racionales con raíces reales
simples:
𝑥3 − 2𝑥2 − 3𝑥 + 10
𝑥2 − 1
𝑑𝑥

2. Vídeo tutorial FdeT:
Problemas resueltos: integrales
Repaso:
Si tenemos que hallar la integral indefinida de una función racional, es decir tenemos
que hallar
𝑝(𝑥)
𝑞(𝑥)
𝑑𝑥
Donde p(x), q(x) son polinomios.
Si el grado de p(x) es mayor o igual que el grado de q(x) entonces podemos dividir esos
polinomios, de forma que tenemos:
𝑝 𝑥 𝑞 𝑥
𝑟 𝑥 𝑐(𝑥)
De esta forma si usamos que p(x)=q(x)c(x)+r(x), dividiendo por q(x) se tendría
𝑝(𝑥)
𝑞(𝑥)
=
𝑞 𝑥 𝑐(𝑥)
𝑞(𝑥)
+
𝑟(𝑥)
𝑞(𝑥)

3. Vídeo tutorial FdeT:
Problemas resueltos: integrales
𝑝(𝑥)
𝑞(𝑥)
=
𝑞 𝑥 𝑐(𝑥)
𝑞(𝑥)
+
𝑟(𝑥)
𝑞(𝑥)
Por lo tanto,
𝑝(𝑥)
𝑞(𝑥)
= 𝑐 𝑥 +
𝑟 𝑥
𝑞 𝑥
𝑝(𝑥)
𝑞(𝑥)
= 𝑐 𝑥 𝑑𝑥 +
𝑟(𝑥)
𝑞(𝑥)
𝑑𝑥
Por lo tanto hemos transformado la integral de la función racional que teníamos
al principio en la suma de una integral de una función polinómica (inmediata de
calcular) y de otra integral racional, pero en la que el grado del numerador es
menor que el grado del denominador.
Por lo tanto nuestro mayor problema ahora es centrarnos en cómo calcular la
integral
𝑟(𝑥)
𝑞(𝑥)
𝑑𝑥

4. Vídeo tutorial FdeT:
Problemas resueltos: integrales
Para hallar la integral
𝑟(𝑥)
𝑞(𝑥)
𝑑𝑥, en primer lugar consideramos el polinomio q(x), y
hallamos sus raíces.
Pueden ocurrir:
1. Las raíces de q(x) son todas reales simples.
2. q(x) tiene raíces reales múltiples.
3. q(x) tiene raíces complejas simples
4. q(x) tiene raíces complejas múltiples.
En este vídeo vamos a abordar el primer caso, es decir el caso en que todas las raíces
de q(x) son reales simples.
Supongamos que las raíces de q(x), son: 𝑥1, 𝑥2, … , 𝑥 𝑛
Entonces la expresión
𝑟(𝑥)
𝑞(𝑥)
se puede expresar de la forma:
𝑟(𝑥)
𝑞(𝑥)
=
𝐴
𝑥 − 𝑥1
+
𝐵
𝑥 − 𝑥2
+ ⋯ +
𝐿
𝑥 − 𝑥 𝑛

5. Vídeo tutorial FdeT:
Problemas resueltos: integrales
Si ahora tomamos integrales, se tiene que:
𝑟(𝑥)
𝑞(𝑥)
𝑑𝑥 =
𝐴
𝑥 − 𝑥1
𝑑𝑥 +
𝐵
𝑥 − 𝑥2
𝑑𝑥 + ⋯ +
𝐿
𝑥 − 𝑥 𝑛
𝑑𝑥
Y por lo tanto tenemos que:
𝑟(𝑥)
𝑞(𝑥)
𝑑𝑥 = 𝐴 𝑙𝑛 𝑥 − 𝑥1 + 𝐵 𝑙𝑛 𝑥 − 𝑥2 + ⋯ + 𝐿 𝑙𝑛 𝑥 − 𝑥 𝑛 + 𝐾
Veamos a continuación cómo se resuelve en un caso práctico. Vamos a resolver la
integral
𝑥3
− 2𝑥2
− 3𝑥 + 10
𝑥2 − 1
𝑑𝑥

6. Vídeo tutorial FdeT:
Problemas resueltos: integrales
Cálculo de
𝒙 𝟑−𝟐𝒙 𝟐−𝟑𝒙+𝟏𝟎
𝒙 𝟐−𝟏
𝒅𝒙
En primer lugar observamos que el grado del numerador es mayor que el del
denominador por lo que tenemos que realizar la división:
𝑥3 − 2𝑥2 − 3𝑥 + 10 𝑥2 − 1
−𝑥3
+ 𝑥 𝑥 − 2
−2𝑥2 − 2𝑥 + 10
2𝑥2
−2
−2𝑥 + 8
Por lo tanto se tiene que
𝑥3
− 2𝑥2
− 3𝑥 + 10 = 𝑥2
− 1 𝑥 − 2 + −2𝑥 + 8
De donde dividiendo por 𝑥2
− 1, se tiene:

7. Vídeo tutorial FdeT:
Problemas resueltos: integrales
𝑥3
− 2𝑥2
− 3𝑥 + 10
𝑥2 − 1
=
𝑥2
− 1 𝑥 − 2
𝑥2 − 1
+
−2𝑥 + 8
𝑥2 − 1
Y simplificando esa expresión obtenemos:
𝑥3
− 2𝑥2
− 3𝑥 + 10
𝑥2 − 1
= (𝑥 − 2) +
−2𝑥 + 8
𝑥2 − 1
Por lo tanto:
𝑥3
− 2𝑥2
− 3𝑥 + 10
𝑥2 − 1
𝑑𝑥 = 𝑥 − 2 𝑑𝑥 +
−2𝑥 + 8
𝑥2 − 1
𝑑𝑥

8. Vídeo tutorial FdeT:
Problemas resueltos: integrales
Tenemos que hallar las dos integrales en las que se ha descompuesto la integral
original.
1. 𝑥 − 2 𝑑𝑥 =
1
2
𝑥2 − 2𝑥
2.
−2𝑥+8
𝑥2−1
𝑑𝑥
Para realizar esta integral debemos factorizar el denominador:
𝑥2
− 1 = 0 𝑥 = ±1
Por lo tanto la factorización del denominador será:
𝑥2
− 1 = (𝑥 − 1)(𝑥 + 1)

9. Vídeo tutorial FdeT:
Problemas resueltos: integrales
Ahora realizamos la descomposición de la fracción
−2𝑥+8
𝑥2−1
en factores simples como
sigue:
−2𝑥 + 8
𝑥2 − 1
=
𝐴
𝑥 − 1
+
𝐵
𝑥 + 1
Nótese que hay tantos sumandos como factores tenga la descomposición factorial
del denominador.
Ahora debemos hallar las constantes A y B, para ello realizamos la suma e igualamos
como sigue:
−2𝑥 + 8
𝑥2 − 1
=
𝐴(𝑥 + 1)
(𝑥 − 1)(𝑥 + 1)
+
𝐵(𝑥 − 1)
(𝑥 − 1)(𝑥 + 1)
Es decir
−2𝑥 + 8
𝑥2 − 1
=
𝐴 𝑥 + 1 + 𝐵(𝑥 − 1)
(𝑥 − 1)(𝑥 + 1)

10. Vídeo tutorial FdeT:
Problemas resueltos: integrales
Nótese que los denominadores son iguales, ya que: 𝑥2
− 1 = (𝑥 − 1)(𝑥 + 1)
Por lo tanto los numeradores también lo serán, es decir:
−2𝑥 + 8 = 𝐴 𝑥 + 1 + 𝐵 𝑥 − 1
De donde dando valores a x obtenemos los valores de las constantes A y B
respectivamente.
(Para dar valores, es conveniente dar a la x los valores de las raíces extraídas
anteriormente para simplificar los cálculos)
Para x= 1, se tiene que: 6 = 2𝐴 𝐴 = 3
Para x= - 1, se tiene que: 10 = −2𝐵 𝐵 = −5

11. Vídeo tutorial FdeT:
Problemas resueltos: integrales
Por tanto se tiene que:
−2𝑥 + 8
𝑥2 − 1
=
3
𝑥 − 1
−
5
𝑥 + 1
Ahora tomando integrales llegamos a.
−2𝑥 + 8
𝑥2 − 1
𝑑𝑥 =
3
𝑥 − 1
𝑑𝑥 −
5
𝑥 + 1
𝑑𝑥 = 3𝐿 𝑥 − 1 − 5𝐿|𝑥 + 1|
Por lo tanto la integral del ejercicio sería:

12. Vídeo tutorial FdeT:
Problemas resueltos: integrales
𝑥3−2𝑥2−3𝑥+10
𝑥2−1
𝑑𝑥 = 𝑥 − 2 𝑑𝑥 +
−2𝑥+8
𝑥2−1
𝑑𝑥=
1
2
𝑥2
− 2𝑥 + 3𝐿 𝑥 − 1 − 5𝐿 𝑥 + 1 + 𝐾
Y en consecuencia.
𝑥3
− 2𝑥2
− 3𝑥 + 10
𝑥2 − 1
𝑑𝑥 =
1
2
𝑥2
− 2𝑥 + 3𝐿 𝑥 − 1 − 5𝐿 𝑥 + 1 + 𝐾