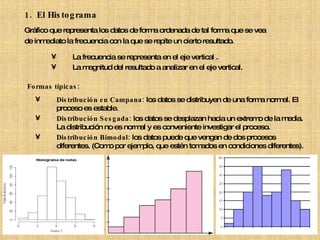
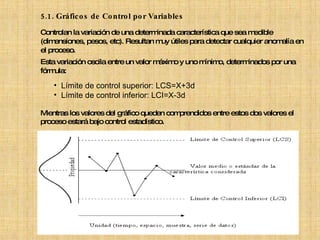
El documento describe diferentes técnicas estadísticas para la gestión de la calidad como histograma, polígono de frecuencias, control estadístico de procesos, estadística básica, gráficos de control y planes de muestreo. Explica cómo estas técnicas permiten analizar y controlar la variabilidad en los procesos de producción para asegurar que los productos cumplen las especificaciones.

1. TEMA 10: TÉCNICAS ESTADÍSTICAS PARA LA GESTIÓN DE LA CALIDAD

2. 1. El Histograma Gráfico que representa los datos de forma ordenada de tal forma que se vea de inmediato la frecuencia con la que se repite un cierto resultado. La frecuencia se representa en el eje vertical . La magnitud del resultado a analizar en el eje vertical. Formas típicas: Distribución en Campana: los datos se distribuyen de una forma normal. El proceso es estable. Distribución Sesgada: los datos se desplazan hacia un extremo de la media. La distribución no es normal y es conveniente investigar el proceso. Distribución Bimodal: los datos puede que vengan de dos procesos diferentes. (Como por ejemplo, que estén tomados en condiciones diferentes).

3. 2. Polígono de Frecuencias Si unimos con una línea los puntos medios de las barras verticales de un histograma, se obtiene la cuerva. Cuando la distribución de frecuencia es uniforme y tiende hacia la media central, se conoce a este forma como Campana de gauss . 3. Control Estadístico de Procesos (SPC) En un proceso interviene multitud de variables. Dado que estos factores no actúan siempre de la misma forma, aparecen fluctuaciones en las características del producto en el proceso. El SPC permite prever estas variaciones y mantenerlos en unos límites razonables para el conjunto del procesos de organización. Podemos clasificar las variables en 2 grupos: Controlables y No Controlables .

4. Variables controlables (causas asignables): son variables que se pueden identificar y es conveniente descubrir y eliminar. Ejemplo: fallos de desgaste, desajuste de máquinas. Variables no controlables (causas no asignables) : variables de tipo aleatorio difíciles de controlar. Ejemplo: Cambio de temperatura ambiente, presión ambiental... - Cuando un proceso es afectado únicamente por una serie de variables aleatorias producidas por causas no asignables, se dice que el proceso está bajo control estadístico . - Cuando además de las causas no asignables aparecen en el proceso variaciones debido a causas asignables el proceso está fuera de control estadístico.

5. 4. Estadística Básica Con la estadística es posible pronosticar o prever la variabilidad de un proceso sin necesidades de medir o conocer las características de todos los productos que se producen a la salida. 1. Media Aritmética Dados los n números a1,a2, ... , an , la media aritmética se define simplemente como: 2. Desviación Típica Es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable. 3. Distribución Si el proceso se comporta de forma controlada, la distribución de los resultados de la muestra se aproximará a la distribución normal o de Campana de Gauss. Se recurre a controlar una muestra de los productos y después se extrapolan los resultados y se averigua si las variaciones de las características del producto están dentro de unos márgenes aceptables.

6. 5. Gráficos de Control Es un gráfico de tipo lineal en el que se representa a lo largo del tiempo el estado del proceso que se desea controlar. En el eje horizontal (X) se indica el tiempo y en el vertical (Y) se representa el indicador de la variable cuya calidad se está midiendo o controlando. Se le añaden dos líneas horizontales con los límites superior e inferior de control, es decir los valores máximos y mínimos que el objeto del análisis puede presentar (tolerancia), así como una línea central. Gráficos de control por variables. Gráficos de medias/ recorridos. Gráficos de control por atributos. Pueden ser:

7. 5.1. Gráficos de Control por Variables Controlan la variación de una determinada característica que sea medible (dimensiones, pesos, etc). Resultan muy útiles para detectar cualquier anomalía en el proceso. Esta variación oscila entre un valor máximo y uno mínimo, determinados por una fórmula: Límite de control superior: LCS=X+3d Límite de control inferior: LCI=X-3d Mientras los valores del gráfico queden comprendidos entre estos dos valores el proceso estará bajo control estadístico.

8. 5.2. Gráficos de Medias/Recorridos Gráfico de medias (X): Se realizan sobre las medidas obtenidas en cada muestra, no por unidad. Gráfico de recorridos (R): Se traza el comportamiento del recorrido de cada una de las muestras. En la práctica se suele recurrir a algún programa de ordenador especializado en el que el control estadístico de la Calidad dado lo extenso de sus cálculos. Algunos programas son: SPSS (www.spss.com/spain), Qstat, STATGRAPHICS (www.statgraphycs.com), MINITAB (www.minitab.com/spanish), ISOSYSTEM SPC (www.isosystem.com.ar).

9. Controlan si el elemento inspeccionado cumple o no unas determinadas condiciones (conforme - no conforme, pasa - no pasa, funciona - no funciona, etc). Muy útil cuando lo que se desea controlar es más difícil de cuantificar con una medida (arañazos en la superficie, presencia de golpes, medidas controladas con un calibre tipo pasa o no pasa. Suele hacerse cuando los fallos ya se han producido, es decir, al final del proceso. Son necesarios para asegurar la calidad final del producto acabado. Más cercana a la idea de Control de Calidad que con la de Calidad Total. Existen varios tipos de éstos gráficos siendo los más habituales los de porcentajes de unidades no conformes (p%). 5.3. Gráficos de Control por Atributos 6. Capacidad de Proceso y de Máquinas Un proceso o máquina es válido cuando los productos que se obtienen de ellas cumplen con las especificaciones. En la práctica, si queremos que un proceso produzca de forma eficiente solemos fijar una tolerancia (un margen de error) de fabricación. Es posible diseñar un proceso estable que esté bajo control, en el cual el límite de control superior (LCS) sea mayor que el límite superior tolerable (LTS).

10. 6.1. Índice de Capacidad Si somos capaces de diseñar un proceso en el que el LTS y el LTI son más pequeños que el intervalo de 6 veces la desviación típica, podremos asegurar que el 99´973 % de los productos se encuentran en la zona de tolerancia, y el proceso sería válido si el índice de capacidad es mayor o igual a 1´33, siendo no válido si es menor que 1´33. 7. Planes de Muestreo La única manera de garantizar que todos los productos son correctos sería inspeccionando el 100% de la producción, pero como esto no es factible recurrimos a técnicas estadísticas de muestreo consistentes en tomar una pequeña muestra de forma aleatoria de un lote de productos e ir mirando si cumplen las especificaciones. El lote será aceptado o rechazado en función del número de unidades que hayan cumplido las especificaciones. Existen dos tipos de muestreo: Planes de muestreo por atributos: Se comprueba el número de productos que no son conformes. Planes de muestreo por variables: Se comprueba el número de productos que no cumplen con algunas de las características en sus especificaciones.

11. 7.1. Planes de Muestreo según Norma UNE 66020 Esta norma se utiliza para establecer el número de unidades que será necesario inspeccionar según el tamaño del lote. Existen varios niveles de inspección: Inspección general: Se usa en la mayoría de los casos. - Nivel I: Nivel reducido, se aplica cuando hay evidencias de buen comportamiento del suministro. - Nivel II: Nivel normal, aconsejado para productos nuevos. - Nivel III: Nivel riguroso, se utiliza cuando hay evidencias de falta de calidad. Inspección especial: Se utiliza en casos muy excepcionales. El Nivel de Calidad Aceptable (NCA), es el porcentaje máximo de unidades no conformes aceptables por lote. 7.2. Tipos de muestreo Muestreo simple: Se hace sobre una sola muestra. Muestreo doble: Se contempla la posibilidad de contemplar una segunda muestra. Muestreo múltiple: Se contempla la posibilidad de contemplar más de dos muestras.