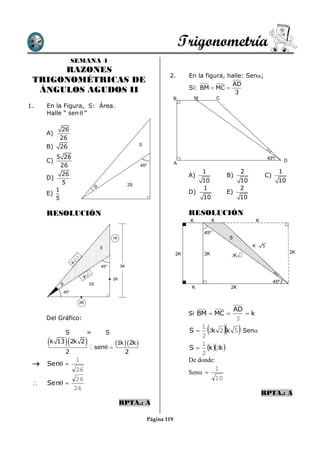
Este documento presenta 5 problemas de trigonometría que involucran el cálculo de senos, cosenos y áreas de figuras geométricas. El primer problema pide calcular senθ dado un triángulo. El segundo calcula senα para un triángulo isoceles. El tercero encuentra la altura de un trapecio. El cuarto calcula el área de una región triangular extendida. Y el quinto calcula el área de un triángulo en términos de θ.

1. Trigonometría
SEMANA 4
RAZONES
2. En la figura, halle: Sen;
TRIGONOMÉTRICAS DE AD
ÁNGULOS AGUDOS II Si: BM  MC 
3
B M C
1. En la Figura, S: Área.
Halle “ sen  ”
26
A)
26
B) 26 S

5 26 45º
C) D
26 45º A
26 1 2 1
D) A) B) C)
5 10 10 10
2S
 1 2
1 D) E)
E)
5 10 10
RESOLUCIÓN RESOLUCIÓN
K K K
45º
1K S
S K 5
2K 2K 2K
2K 2
13
K
45º 3K
2 
2K 2K
45º
 2S
K 2K
45º
2K
AD
Si BM  MC  k
Del Gráfico: 3
S = S S
1
2

2k 2 k 5 Sen  
k 
13 2k 2  sen 
1k  2k  1
S  k 2k 
2 2 2
1 De donde:
 Sen 
26 1
Sen 
26 10
 Sen 
26
RPTA.: A
RPTA.: A
Página 119

2. Trigonometría
3. Se tiene un trapecio cuyas RESOLUCIÓN
diagonales son perpendiculares y
sus bases miden 4 y 12. D
Halle la altura de dicho trapecio si
el producto de sus diagonales es 2c
80. B
S1
 a
A) 4 B) 5 C) 6 c
D) 7 E) 8
S
RESOLUCIÓN A b C
4a
4
Si: S=64 E
d2 d1 h 1
acSen  64  acSen = 128
2
Se pide:
1
12 S1  2c  5a Sen
2
Dato: d1.d2  80  5acSen
Se pide:  S1  6402
1 RPTA.: B
S= d1d2 Sen90º
2
5. En la figura mostrada, evaluar el
1
S= 4  12h área de la región triangular AOB
2 en términos de 
De donde: 80 =16h
h=5
RPTA.: D
B
4. El área de un triángulo ABC es
64 2 , se prolongan AB y BC
hasta los puntos D y E

A 4 o 4
respectivamente de tal manera
A) 4Sen B) 8Sen2
que AD =3 AB  CE = 4 BC .
C) 2Cos 
2 D) 5Sen
Halle el área de la región
E) 3Cos 
2
triangular DBE
A) 6382 B) 6402 C) 6422 RESOLUCIÓN
D) 6442 E) 6502 4 Sen2

4
S
 2
A 4 o
Página 120

3. Trigonometría
1 (1) = (2)
De la figura: S   4  4Sen2
2 130 Sen  9
 S  8Sen 2 2
9 130
RPTA.: B Sen   Csc 
130 9
RPTA.: C
6. Si ABCD es un cuadrado, donde:
CD  3ED y además: m BEA   , 7. En la figura ABCD es un cuadrado,
Calcule: Csc M y N son puntos medios.
Determine "cot " .
C E D
 A B
M

B A
D N C
110 121 130 A) 2 B) 1 C) 3
A) B) C)
3 4 9 1 1
D) E)
145 160 2 3
D) E)
10 12
RESOLUCIÓN
RESOLUCIÓN
2a a


3a
a
3a
13
a 2
10a
2a
S
45º
a 2 a 2
a
a
3a
1 9a2
S  3a3a  …(1) De la figura: Cot  3
2 2
RPTA.: D
También:
S
1
2
13a  
10a Sen …(2)
Página 121

4. Trigonometría
8. Del gráfico, halle “x”, en términos
de “”. A) mctg  tg
B) m  tg  ctg 
C) mctg  tg
1

D) mtg  ctg
1
3
E) m.ctg  tg
RESOLUCIÓN
2

x
X
A) 3cos   2Sen
B) 2 cos   3Sen 
C) 2sen  3cos xctg xtg
m
D) 3sen  2cos
E) 2sen  3cos Del grafico: xCtg  xtg  m
x Ctg  tg   m
RESOLUCIÓN
 x  mctg  tg
1
3Sen
 RPTA.: C
10. En la figura, halle el perímetro del
3
 rectángulo OABC si se conoce “  ”,
y el radio del cuadrante MON es
“r”.
2 B C


x N
2Cos
 x  3Sen  2Cos
RPTA.: D
r
9. En la figura, halle “X” en términos
de ””, “  ” y “m”. A M O
 A) 2r  sen  cos
B) r  csc  sen
C) r  sen  cos
X
D) 2r  csc  sec

E) r2 sec csc
m
Página 122

5. Trigonometría
RESOLUCIÓN B
r Csc 
B C 

E
r Sec  r Sec  
A D C
r
m


A  BED: DE = m.Cos.Sen2
r Csc 
RPTA.: E
 Perímetro del rectángulo
OABC= 2R  csc  sec
12. A partir de la figura mostrada, se
RPTA.: D pide determinar M, si:
11. En la figura halle DE en términos
de “m” y “”. 2
B
3S
1
E
 
S
 9 Cot  Tag
M y S
A D 4 Cot  Tag
m
representa área
A) m sen csc 1 2 1
A) B) C)
B) m cos sen 2 3 5
3 1
C) m cos2 sen2 D) E)
2 4
D) m cos2 sen
E) m cos sen2 RESOLUCIÓN
RESOLUCIÓN
2
ABC = AB = mCCos
3S
ADB = BD = mCos . Sen
S 1
 
Cot
3Cot
Página 123

6. Trigonometría
1 1 1
4S  3Ctg (3) … 1  1+ = tg² + tg +
2 4 4
1 5  1
2
S  Cot  (1) … 2    tg  
2 4  2
2 en 1
5 1 5 1
  tg   tg 
4 3 2 2 2
.Cot  (3)Cot RPTA.: B
2 2
 4Cot=9Cot 
14. Desde un punto en tierra se
4 observa lo alto de un edificio con
Tan= . tan
9 un ángulo de elevación de 37º .
9 Cot  Tan Nos acercamos una distancia “x” y
M
9 4 el ángulo de elevación tiene por
4 Cot  (Tan) tangente 4. Si la altura del
4 9
edificio es “h”.
9 Cot  Tan 3 x
M=  Halle:
2 2 h
6 Cot  Tan
3 (Tomar: sen 37º = 0,6)
RPTA.: D
A) 1,21 3 B) 1,08 2 C) 1,08 3
13. Una hormiga observa lo alto de un D) 2,13 2 E) 3,01 5
poste con un ángulo de elevación
“”, si se acerca hacia él una RESOLUCIÓN
distancia igual a su altura y mira
lo alto de dicho poste
nuevamente, el nuevo ángulo de
elevación es el complemento del
anterior. Halle: “tg”.
h=3k
5 1 5 1
A) B)
2 2
C) 5 +1 D) 5 1  
E) 5 x 4k-x
Dato: tg  4
RESOLUCIÓN 3k
4
4k  x
3k  16k  4x
4x  13k
Del gráfico:
Hctg =
Se pide:
H + Htg  H  ctg   H 1  tg 
x 4x 13k
1    1,083
  1  tg  1 = tg + tg² h 4h 4(3k)
tg RPTA.: C
Página 124

7. Trigonometría
RESOLUCIÓN
15. Desde un punto de tierra se ve lo
alto de una torre con un ángulo de
elevación “  ”. Nos acercamos una
distancia igual a la altura de la 15m
torre y el ángulo de elevación es
ahora 37º. Calcule: ctg
(Tomar: sen37º = 0,6)
5 4 7
A) B) C)
3 3 3 H
D) 3 E) 2
 
RESOLUCIÓN
a
tan=0,76
tan  =0,19
H=3k  tan=4tan 
15+H =atan
H= a tan 
 37º
15  H tan
4k   4
H H tan
7k 7  15+H = 4H.
Se pide: ctg  
3k 3  H = 5m
RPTA.: B
RPTA.: D
17. Un avión que esta por aterrizar
16. Una antena de radio de 15m. de observa en su misma trayectoria
longitud se encuentra en la azotea la pista de aterrizaje de extensión
de un edificio. Desde un punto del igual al doble de la altura a la que
plano horizontal que pasa por la se encuentra, si ve el extremo
base del edifico las elevaciones más alejado con ángulo de
angulares de la parte superior e depresión de 22º30’ .Calcule con
inferior de la antena son “” y “  ” que ángulo observa el otro
respectivamente. Si: tan = 0,76 extremo.
y tan  =0,19, determinar (en m) A) 22º30’ B) 67º30’ C) 90º
D) 60º E) 120º
la altura del edifico.
A) 4 B) 5 C) 6
D) 7 E) 8
Página 125

8. Trigonometría
RESOLUCIÓN h  AD Sen º
60
A Horizontal AD  AB  40
 22º30' 3
h  40  h  34.6 m
2
m RPTA.: D
19. Subiendo por un camino inclinado
 22º30'
G F 2m E un ángulo de 37º respecto a la
FE  2m horizontal, se divisa lo alto de un
poste con un ángulo de elevación
FEA  22º30'
de45º. Si el poste se encuentra a
AGE: GE=mctg 22º30’ 20m del punto de observación;
¿Cuál es la altura del poste?
GE  m  2H  A) 2m B) 3m C) 6m
D) 4m E) 8m
 GF  GE  FE
RESOLUCIÓN
GF  m  
2H  2m  m  2  1 Poste
GE m  2  1
AGF cot = 
AG m 45º
cot = 2  1 h=?
 = 67º 30
´ RPTA.: D
Punto de
18. Una persona colocada a la orilla 20m 53º
observación
45º 12m
del rio ve un árbol plantado sobre
37º
la ribera opuesta bajo un ángulo
37º 16m
de elevación de 60º se aleja
40mts, y nuevo ángulo de Del gráfico: h  12  16
elevación mide 30º ¿Cuál es la h  4m
altura del árbol? RPTA.: D
A) 43,6 B) 30,6 C) 34,6
20. Halle “ Csc ” del gráfico:
D) 36,4 E) 38,4
RESOLUCIÓN 5u 9u
D
 53º
30 30
h
60 30
C A 40 B (Tomar sen 37º = 0,6)
Página 126

9. Trigonometría
56 33 65
A) B) C)
65 65 56
65 15
D) E)
33 14
RESOLUCIÓN
Del gráfico: S = S
1412  1315 Sen
2 2
56
Sen 
65
65
 Csc 
56
RPTA.: C
Página 127