Este documento presenta un índice de los temas que se abordarán en el curso de álgebra de 4to año de secundaria. Incluye 9 temas principales que son: sucesiones y progresiones, funciones, logaritmos, ecuaciones con valor absoluto, ecuaciones de grado superior, inecuaciones de grado superior, inecuaciones con valor absoluto, sistema de inecuaciones y el binomio de Newton. Cada tema contiene diferentes capacidades y conceptos que se desarrollarán.

1. Índice
ÁLGEBRA - 4 to AÑO DE SECUNDARIA
Pág.
T E M A 1 Sucesiones y Progresiones ....................................................................... 2
Sucesiones ................................................................................................................................... 2
Progresiones Aritméticas ...................... 5
Progresiones Geométricas.............................................................................................................. 8
T E M A 2 Funciones................................................................................................... 11
Relaciones Binarias ....................................................................................................................... 11
Clases de Relaciones .................................................................................................................... 17
Función ..................................................................................................................................... 25
Dominio y Rango de una Función................................................................................................... 31
Gráfica de Funciones .................................................................................................................... 38
T E M A 3 Logaritmos................................................................................................. 51
T E M A 4 Ecuaciones con Valor Absoluto................................................................. 60
T E M A 5 Ecuaciones de Grado Superior .................................................................. 63
T E M A 6 Inecuaciones de Grado Superior............................................................... 70
Inecuaciones Lineales ................................................................................................................... 70
Inecuaciones Cuadráticas............................................................................................................... 73
Inecuaciones de grado superior...................................................................................................... 75
T E M A 7 Inecuaciones con Valor Absoluto ............................................................. 78
T E M A 8 Sistema de Inecuaciones........................................................................... 81
T E M A 9 Binomio de Newton................................................................................... 84
Factorial de un Número ................................................................................................................ 84
Números Combinatorios ................................................................................................................ 86
Binomio de Newton ...................................................................................................................... 92

2. Álgebra  I.E.P. Corpus
Christi
Tema nº 01: SuceSioneS y progreSioneS
Capacidades:
 Resuelve problemas con sucesiones.
 Calcula el término “n” ésimo de una progresión geométrica y aritmética.
 Calcula la suma de términos de una progresión geométrica y aritmética.
 Resuelve problemas, aplicando propiedades de una progresión aritmética y geométrica.
Exploración y Desequilibrio:
 En una competencia de tiros al blanco dan las siguientes listas de números:
a) 5; 9 ; 11; 15 ............
b) 3; 6; 9; 12; .........
c) -5; -1; 3; 7 ...............
d) a; 3a; 5a; 7a; .........
 ¿En cuál de ellas, la razón entre cada par de términos es la misma?
 ¿Qué letra continua? A; D; G; J;.....
 Calcule es sexto término de la sucesión:
4; 6; 11; 21; 38;…………
 ¿Qué letra continua? C; O; R; P; U; S; .....
Desarrollo del Tema:
1. Sucesión: Se llama sucesión a la secuencia ordenada de términos, regidos por una ley de
formación.
Ejemplo:
5; 12; 19; 26; 33; . . . . .
2; 6; 18; 54; 162;. . . . . .
4; 9; 16; 25; 36;. . . . . .
A; D; H; M; ………….
2. Sucesión Aritmética Lineal o de 1er Orden:
Es cuando la razón es constante en la primera línea, también se le llama progresión
aritmética (P.A.)
Si: t1; t2 ; t3 ; t4 ; t5 ;……….tn (razón constante)
t tn = t 1 +
Donde: r(n-1) ó
t = t 0 + r.n
tn :n Término enésimo
t1 : primer término
r : razón
n : número de término
t0 : término anterior al primero
3.- Sucesión Cuadrática o de 2º Orden:
t tn = an2 +
bn + c
Regla práctica para calcular el término enésimo de una sucesión cuadrática:

3. Ecuación Segundo Año
Si: t0 ; t1; t2 ; t3 ; t4 ; t5 ;……….tn
l m n p q
r r r r
Donde : a = r/2
b=l–a
c = t0
Sucesión Geométrica:
t tn = t1 x
qn-1
Donde:
tn : Término enésimo
t1 : primer término
r : razón geométrica
n : número de término
Sucesión Armónica o Progresión Armónica:
t 2t n-1 x
2tn+1
Sucesiones Polinomiales de Orden mayor que dos:
t tn =
Se usará el método más práctico que es el: uso de los números combinatorios
2t n-1+2tn+1
n!
Cn =
k
( n − k ).! xk!
ºSi: t1; t2 ; t3 ; t4 ; t5 ;……….tn
a b c d e…….
m n p q ……
r r r
n-1 n-1 n-1 n-1
El enésimo término se calcula así: tn = t1 C + a.C + m.C + r.C
0 1 2 3
prÁcTica DirigiDa
1) ¿Qué término sigue?
4; 5; 10; 19; 32;…. 5) 1, 5; 4; 8; 9; 11; x; y . Hallar x+y
a) 49 b) 27 c) 32 d) 35 e) 37 a)14 b) 16 c) 30 d) 27
2) Hallar x + y, en la sucesión 6) 1/2; 1/2; 1; 3; 12; 60; ......
8; 7; 10; 9; 12; 11: x; y a) 360 b) 630 c)120 d)180
a) 20 b) 25 c) 22 d) 27 e) 25
7) 2, 5; 9; 15; 16; 45; 23; x; y. Hallar
3) ¿Qué número continua? x-y
19; 38; 36; 72; 70; 140; x a)135 b) 105 c)30 d)72
a)280 b)210 c)122
d)138 e)125 8) A, D; I; O; . . . .
a)Y b) X c) V d) W
4) ¿Qué letra continua?
B; K; E; O; H; S; K; ? 9) En la sucesión cuántos términos acaba
a) X b) Y c) V d) W e) S en 5.
Prof.: Rodolfo Angel Carrillo Velásquez
3

4. Álgebra  I.E.P. Corpus
Christi
11; 24; 37; 50;……;2598 a)840 b)843 c)942 d)823 e)834
a) 20 b) 42 c) 28 d) 30 e) 25
18)Busca información del tema de
10)¿Cuál es el término más cercano a Sumatorias y relaciona sus fórmulas
1000 que pertenece a la progresión con las referentes a Progresión
aritmética? Geométrica.
20; 39; 58; 77;….
a)999 b)989 c)908 ENCUENTRA EN CADA CASO EL NÚMERO QUE SIGUE:
d)1008 e)1029
19)5; 6; 9; 17; 34; ......
11)¿Cuántos términos tiene la siguiente a) 65 b) 60 c) 75 d) 59
sucesión de primer orden?
12n; 17n; 24n; 31n;........ 620n
20) 6, 7; 13; 20; 33; 53; . .
a) 73 b) 75 c) 77 d) 79 e) 81
a)73 b) 86 c) 90 d) 70
12)Si la siguiente sucesión:
9/4; 17/9; 27/16; 39/25;...... 21)3; 6; 11; 19; 31; .....
Tiene 20 términos. Determinar la a) 47 b) 48 c) 36 d) 52
diferencia de los términos de la última
fracción. 22)1; 1; 1; 2; 12; .....
a) 54 b) 70 c) 76 d) 62 e) 64 a) 250 b) 160 c) 288 d)24
13)Hallar el término de lugar ba de la 23) E; G; K; P;.....
siguiente P.A: a) Y b) V c) X d) W
a8b; a93; b04; ba5;....
a) 302 b)303 c)352 d)402 e)403
24) B, F; I; M; O...
14)Dada la sucesión de primer orden: a)R b) S c) T d) V
a2 + 1; 7a; 9a - 1;....
Hallar el primer término que contenga 3 25) 17; 29; 48; 76; 116; 172; ….
cifras. a) 249 b) 237 c) 194 d) 227
a)102 b)105 c)108 d)107 e)109
26)3, 6; 18; 66; ....
15)Calcular el último término de la fila 30 a)192 b) 258 c)266 d)272
del siguiente triángulo numérico:
1
27)40, 37; 33; 26; 14; . . . . .
3 5
5 7 9 a)-19 b) -5 c)-10 d) 0
7 9 11 13
9 11 13 15 17 28)1, 4; 3; -1; 9; -4; 27; . . . .
............................................. a)5 b) 10 c) -5 d)16
a)140 b)120 c)118 d)117 e)108
29)-2, -1; 1; 5; 13; . . . .
16)En el triángulo numérico, hallar la suma a)50 b) 29 c)25 d) 35
del primer y último término de la fila
20. 30)D; G; J; M; X; U; R ; ….
1 ….. F1 a) Ñ B) O C) P D) F
3 5 ….. F2
7 9 11 ….. F3
13 15 17 19 …. F4 31) 5, .?; 32; 68; 140; 284
21 23 25 27 29...... F5 a) 14 b) 10 c) 12 d) 20
.............................................
a)900 b)450 c)801 d)702 e)800 32)El número equivocado en: 2; 5, 10;
12; 26; 29; 58; 61; 122; es:
17)Calcular el término 30 de la sucesión: a)5 b) 10 c) 12 d) 26
2; 3; 6; 11;...................
progreSioneS ariTmÉTicaS

5. Ecuación Segundo Año
Exploración y Desequilibrio:
 En un test de capacidad se dan las siguientes listas de números:
a) 3; 7 ; 11; 15; ............
b) 3; 6; 9; 12;.........
c) 4; 12; 20; 28; 34; 42………
d) -5; -1; 3; 7;...............
 ¿En cuál de ellas, la razón es constante?
 ¿Cuánto es la suma de los 10 primeros números naturales?
 ¿Cuánto es la suma de los 100 primeros números naturales? ¿Será fácil calcularlo?
Desarrollo del Tema:
Progresión: Es una sucesión de números que se caracteriza por aumentar o disminuir una
cantidad en forma constante, llamada razón. Pudiendo ser ésta por diferencia o cociente
Progresión Aritmética: Cuando la razón se obtiene por diferencia
 La progresión aritmética es considerada creciente cuando la razón es positiva.
Ejemplo: 3; 9 ; 15; 21 ............
 La progresión aritmética es considerada decreciente cuando la razón es negativa.
Ejemplo: 30; 26; 22; 18 ............
an = a1 + (n-1)r
n
Fórmulas S n = ( a1 + a n )  
básicas 2
Donde:
 a1 = Primer término
 an = Ultimo término
 n = número de términos
 Sn = Suma de los “n” primeros términos
prÁcTica DirigiDa
1. Tres términos de una P.A, creciente tercero y séptimo término es igual a 8.
tienen como suma 42, y como producto Hallar al término 100 de la P.A.
2 688 el mayor es: a) 185 b) –80 c) –186 d) 200
a) 4 b) 8 c) 16 5. En una P.A. cuyo primer término es 16 la
d)32 suma del cuarto y noveno término es
igual a la semisuma del undécimo y
2. ¿Cuántos múltiplos de 7 existen entre 11 decimoséptimo ¿Cuál es el valor del
y 173? quinto término?
a) 21 b) 22 c) 23 d) 24 a) 24 b) 32 c) 40 d) 48
3. En la P.A: X.....-59, -61, Hallar el número 6. En una P.A. creciente de 7 términos la
de términos, si la suma de todos los suma del 3ro. 4to. y 5to. término es 54 y
términos es nulo. el producto de los términos primero y
a) 62 b)63 c) 64 d)F.D. último es 180. Halla la razón de la P.A.
a)2 b)3 c) 4
4. La suma del segundo y quinto término de d)5
una P.A. es igual a 14; la suma del
Prof.: Rodolfo Angel Carrillo Velásquez
5

6. Álgebra  I.E.P. Corpus
Christi
7. La suma de tres términos de una P.A. es
33. El cuadrado del último térmno excede 19. En la P.A: X.....-59, -61, Hallar el
a la suma de los cuadrados de los dos número de términos, si la suma de
primeros en 11 ¿Cúal de los sgtes no todos los términos es nulo.
pertenece a P.A? a) 62 b)63 c) 64 d)F.D.
a) 8 b)11 c) 14 d) 17
20. La suma del segundo y quinto término
8. Interpolemos, usando la fórmula de an de una P.A. es igual a 14; la suma del
en: tercero y séptimo término es igual a 8.
 5 medios aritméticos entre 8 y 32 Hallar al término 100 de la P.A.
 10 medios aritméticos entre -15 y a) 185 b) –80 c) –186 d) 200
40
 6 medios aritméticos entre -7 y -56 21. En una P.A. cuyo primer término es 16
 7 medios aritméticos entre 5 y 9 la suma del cuarto y noveno término es
igual a la semisuma del undécimo y
9. El duodécimo término de una progresión decimoséptimo ¿Cuál es el quinto
aritmética es 15 y la diferencia común término?
es -3. Determina el primer término. a) 24 b) 32 c) 40 d) 48
10. La diferencia común de una progresión 22. ¿Cuántos términos deben tomarse de la
aritmética es 2/5 y el décimo término es P.A.; -9, -6, -3.......; para que
30. Halla el primer término. la suma sea 66.
a) 9 b) 10 c)11 d)12
11. EL primer término de una progresión
aritmética es 6 y el noveno término es 23. La suma de todos los números naturales
-74. Halla la diferencia común. múltiplos de 6, menores que 200 es:
a)3366 b)3663 c)3636 d)3676
12. Determina la razón “r” de -4; …, 116;
donde 116 es décimo sexto término. 24. ¿Cuántos múltiplos de 13 existen entre
25 y 261?
13. El primer término de una progresión a) 17 b) 18 c) 19 d) 20
aritmética es -42, el enésimo término 6
y la razón es 3. ¿cuál es el número de 25. La suma de los cinco términos de una
términos? progresión aritmética es 315, y la
diferencia entre el quinto y el primero
14. ¿Qué lugar ocupa el número 109 en la es 28, ¿cuál es la progresión?
P.A.: -15; -11; -7; .......?
a) 32 b) 24 c) 16 d)30 26. Un obrero debe depositar una carretilla
de arena, alrededor de cada uno de 30
15. El quincuagésimo (50) múltiplo de 3 es: árboles que están en línea recta,
a) 150 b) 144 c) 141 d)153 separados 6 metros. Si el montón de
arena está a 10m del primer árbol,
16. Tres términos de una P.A, creciente encontrar la distancia recorrida luego de
tienen como suma 42, y como producto realizado el trabajo.
2 688 el mayor es: a) 2910 b)5820 c)11640 d)4045
a) 4 b) 8 c) 16 d)32
17. Halla la suma de los números impares 27. Determinar el término central de una
desde 29 hasta 137. P.A. de 7 términos, Sabiendo que la
a) 4565 b) 4594 c) 4536 d) suma de los términos de lugar impar es
4702 77 y la de los de lugar par es 56.
a) 19 b) 14 c) 16 d)24
18. Halla el número de términos y la suma 28. En una P.A. creciente de 7 términos la
de ellos, en una P.A. cuya razón es 3, suma del 3ro. 4to. y 5to. término es 54
su primer término es 6 y su último y el producto de los términos primero y
término 123. último es 180. Halla la razón de la P.A.
a) 39 y 2577 b) 40 y 2586 a)2 b)3 c) 4 d)5
c) 39 y 2580 d) 40 y 2577

7. Ecuación Segundo Año
29. Desde los puntos A y B distantes entre 39. En una P.A, se cumple:
sí 510 m, se mueven simultáneamente a1 + a5 = 14 , a3 + a6 = 20
dos cuerpos, uno al encuentro del otro.
Calcular a4:
El I de ellos recorre en el primer minuto
50 metros y en cada minuto siguiente a) 3 b) 5 c) 7 d) 9 e) 11
dos metros más que el precedente. El II
cuerpo recorre en el primer minuto 40 40. Si: a, 2a, a2 son los 3 primeros términos
metros y en cada minuto siguiente 4 de una P.A. Calcular la suma de los 10
metros más que el precedente. primeros:
¿Después de cuántos minutos se a) 160 b) 165 c) 166
encuentran estos dos cuerpos?
a) 5 b)15 c) 34 d)30 d) 144 e) 150
30. Sabiendo que el término central de una
P.A. de 40 términos es 22,5. Calcular la 41. El primer término de una P.A. es 5. El
suma de todos sus términos último es 45; y la suma de todos los
a) 900 b) 843 c) 964 d)845 términos es 400. Calcular el # de
términos.
31. ¿Cuántos medios aritméticos se deben a) 14 b) 15 c) 16
interpolar entre 4 y 40 para que la suma
de la P.A. resultante sea de 220? d) 17 e) 18
a)8 b)10 c) 9 d) 5
42. En una P.A. de 25 términos, el décimo
32. El mayor de tres números que forman tercero es igual a 30. La suma de todos
una P.A. es el doble del menor. ¿Cuál es los términos de la P.A es:
el mayor de estos números, si su a) 1250 b) 1000 c) 875
producto es 17496.
a) 36 b) 27 c) 90 d)59 d) 750 e) 700
33. Determinar el décimo quinto término de 43. Hallar la razón de una P.A. de 3
una P.A.. Si la suma de sus “n” términos términos, tales que al adicionar 3; 10 y
está determinado por: Sn = n(n+8). 2 respectivamente se obtenga números
a) 37 b) 43 c) 64 d)45 proporcionales a 2, 4 y 3.
a) 2 b) 4 c) 5
34. Los tres términos en P.A. que
aumentados en 2, 3 y 8 d) 6 e) 7
respectivamente son proporcionales a
10, 25 y 50. ¿Cuál no es uno de sus
términos? 44. Considere una P.A. cuyo sexto término
a) 2 b) 7 c) 12 d)15 es 3/5 del tercer término, que es
positivo, si el producto de los mismos es
35. Si se sabe que a, a2 y 3a son los tres 15. Determinar el número de términos
términos de una P.A. entonces la suma que se debe tomar de esta P.A. para
de los diez primeros términos es: 1
a) 110 b) 84 c) 116 d)124 que sumen 30 .
3
36. La suma de cuatro números racionales
45. Los lados de un triángulo rectángulo forman
en P.A. es 20 y la suma de sus inversos
una progresión aritmética. Hallar la suma de
es 25/4. ¿Cuál de los siguientes no lo
las tangentes de sus dos ángulos agudos.
es?
a)4 b) 6 c) 8 d) 10 46. Se va a pagar una deuda de 150 soles en
letras que forman una progresión aritmética.
37. La suma de tres números en P.A. es El primer pago que se realizará será de 30
22,5. Si al centro se le resta 1,5 se soles y cada pago posterior será dos soles
transforma en una P.G.. Uno de los menos que el pago anterior. ¿En cuántas
números que no pertenece es: letras se terminará de pagar?
a) 7,5 b) 3 c) 12 d)5 a) 6 b) 7 c) 4
38. Busca información del tema de d) 25 e) 19
Sumatorias y relaciona sus fórmulas con
las referentes a Progresión Aritmética
Prof.: Rodolfo Angel Carrillo Velásquez
7

8. Álgebra  I.E.P. Corpus
Christi
progreSioneS geomÉTricaS
Exploración y Desequilibrio:
 En las siguientes listas de números: ¿En cuál de ellas, la razón es constante?
a) 1; 8; 27; 64;...............
b) 3; 6; 12; 24;.........
c) 2; 6; 24; 120;.........
d) 1; 1 ; 1; 1;............
3 9 27
 Calcular la suma de las áreas de todos los cuadrados que se pueden inscribir
sucesivamente a partir de un cuadrado de 1m de lado.
 Una hoja de papel se parte por la mitad; después se superponen las dos mitades y se
vuelven a partir por la mitad, y así sucesivamente. Después de 8 cortes. ¿Cuántos trocitos
de papel habrá?
Desarrollo del Tema:
Progresión Geométrica: Cuando la razón se obtiene por cociente.
an = a1.r n-1
Sn =a.
(r n
−1 )
1
( r − 1)
a1
Pn = ( a1 .a n ) n
S∞ =
(1 − r )
Donde:
 a1 = Primer término
 an = Ultimo término
 n = número de términos
 Sn = Suma de los “n” primeros términos
 Pn = Producto de los n primeros términos
 S∝ = Suma de los infinitos términos
RECUERDA:
Las progresiones geométricas pueden ser CRECIENTES y DECRECIENTES.
Una progresión geométrica es creciente si su primer término es positivo y la razón es
positiva y mayor que 1, y es decreciente si su primer término es positivo y la razón es
positiva y menor que 1.
Si la razón es negativa, los términos de la progresión resultan alternadamente positivo y
negativo; y por lo tanto, uno mayor, uno menor, uno mayor, etc.
Ejemplos:
1) 4; 8; 16; 32; 64; 128; …. es una progresión geométrica creciente; Porque su primer
término es positivo y la razón es 2, positiva y mayor que 1.
2) 81; 27; 9; 3; 1;, …… es una progresión geométrica decreciente; porque su primer
1
término es positivo y la razón es , positiva y menor que 1.
3
3) La progresión geométrica: -1; 5; -25; 125; …. no es creciente ni decreciente, pues la
razón es negativa que es -5.

9. Ecuación Segundo Año
prÁcTica DirigiDa
1. Interpolemos, usando la fórmula de an y que la suma de los dos primeros es
en: igual a 60.
 5 medios geométricos entre 3 y a)60 b) 764 c) 5/3 d) 768
192
 4 medios geométricos entre 5 y 10. Si la suma de los 6 primeros términos de
-1215 una P.G. es igual a 9 veces la suma de los
 5 medios geométricos entre 36 y tres primeros términos, entonces la razón
9/16 es:
 4 medios geométricos entre ½ a) 2 b) 3 c) 4 d)8
y-1/2048
 Dos medios geométricos entre 5 y 11. La diferencia del tercer término menos el
625 sexto de una P.G. es 26 y el cociente es
27. Calcular el primer término
2. El sexto término de una P.G. es 1024 y la a) 243 b) 234 c)5/9 d)1/9
razón es 4. Entonces el tercer término es:
a) 16 b) 4 c) 16 d)64 12. En una P.G. creciente de tres términos se
multiplica el primer término por 4, al
3. Si el producto de tres números que están segundo por 7 y al tercero por 6,
en P.G. es 1000 y la razón es 3. ¿Cúal de obteniéndose una P.A.. Hallar la razón de
los sgtes no pertenece a P.G.? la P.G.
a)10/3 b)10 c) 30 d) 3 a) 2 b) 3 c) 4 d)5
4. La suma de los 3 términos de una P.G. es 13. La suma de los 3 términos de una P.G.
10,5. Si el término medio es tres, hallar la es 10,5. Si el término medio es tres,
razón: hallar la razón:
a) 3,8 b)3,5 c) 1,5 d) 2 a)3,8 b)3,5 c) 1,5 d) 2
5. Calcula el primer término de una P.G. en 14. Calcula el primer término de una P.G.
el que el tercer término es 3 y el séptimo en el que el tercer término es 3 y el
es 3/16 séptimo es 3/16
a) 12 b) 8 c) 1/3 d) 1/9 a) 12 b) 8 c) 1/3 d) 1/9
6. Encontrar el primer término de una P.G. 15. Encontrar el primer término de una P.G.
en la cual el 3ro y 6to término son 1/18 y en la cual el 3ro y 6to término son 1/18
1/486 respectivamente. y 1/486 respectivamente.
a) 2 b) 3 c) 1/3 d) a) 2 b) 3 c) 1/3 d) 1/2
1/2 16. Hallar el número de términos de una
PG. cuyo primer término es 3, sabiendo
7. Los 4 medios geométricos interpolados que la suma de ellos es 1092 y la razón
entre 160 y 5 de una P.G. es: es 3.
A) 5, 10, 20, 40 B) 10, 30, 60, 90 a)6 b) 8 c) 4 d) 5
C) 80, 40, 20, 10 D) 120, 90, 60, 30
17. Los 4 medios geométricos interpolados
8. Hallar el número de términos de una PG.
entre 160 y 5 de una P.G. es:
cuyo primer término es 3, si la suma de
A) 5, 10, 20, 40 B) 10, 30, 60, 90
ellos es 1092 y la razón es 3.
C) 80, 40, 20, 10 D) 120, 90, 60, 30
a)6 b) 8 c) 4 d) 5
18. La diferencia del tercer término menos
el sexto de una P.G. es 26 y el cociente
9. Una P.G. tiene 4 términos, encuentre el es 27. Calcular el primer término
último término si se sabe que la razón a) 243 b) 234 c)5/9 d)1/9
común es igual a 1/3 del primer término
Prof.: Rodolfo Angel Carrillo Velásquez
9

10. Álgebra  I.E.P. Corpus
Christi
19. La cantidad que hay que sumar a 5, 13 transforma en una PG.. Uno de los
y 29, para que formen una P.G. es: números que no pertenece es:
a) 2 b) 3 c) 4 d)5 a) 7,5 b) 3 c) 12 d)5
20. ¿Cuántos antecesores (padre, abuelos, 30. Una PG. admite 4 términos, siendo la
bisabuelos,. . .) tiene una persona suma de sus extremos 27 y los
después de 6 generaciones? centrales 18. ¿Cual de los términos no
a)64 b)126 c) 128 )256 lo es?
a) 24 b) 3 c) 12 d) 5
31. Hallar el mayor de tres números
21. Tres madres impacientes esperan
positivos de una PG., sabiendo que la
consulta con niños de 1, 37, 289 días. El
suma es 26 y la suma de sus inversas
pediatra para entretenerlas, les pide
es 13/18.
que averigüen dentro de cuántos días
a) 18 b) 3 c) 6 d) 15
las edades de sus niños estarán en PG.
a) 5 b) 3 c) 4 d)6
32. Las edades de 4 personas están en P.G.
El producto de todas ellas es 3779136 y
22. ¿Cuántos antecesores el más joven de ellos tiene 24 años.
(padre, abuelos, bisabuelos,...) tiene
una persona después de 10 33. Calcular la suma de las áreas de todos
generaciones? los cuadrados que se pueden inscribir
a) 1024 b) 2048 c) 2046 d) 1349 sucesivamente a partir de un cuadrado
23. Alrededor de un punto se ha construido de 4m de lado
infinitos ángulos, cuyas medidas esta en a) 32m2 b)16m2 c)64m2 d) 48m2
progresión geométrica de razón ½. La
medida del primer ángulo es:
34. Sea una P.G. se tiene: que la razón
a) 90º b) 150º c)120º d) 180º
S5 31
entre: = . Hallar el término 8.
24. Se deja caer una pelota desde una S3 7
altura de 90m, si en cada rebote la
pelota se leva 1/3 de la altura de lo cuál 35. Si se aumenta una misma cantidad a los
cayó la última vez. ¿Qué distancia
números 20, 50 y 100, se forma una
recorre la pelota hasta quedar en
P.G. cuya razón es:
reposo?
a) 1/2 b) 1/3 c) 2
a) 180 b)135 c) 90 d)225
d) 4/3 e) 5/3
25. Los 4 medios geométricos interpolados
36. ¿Cuál es la razón de una PG. de 12
entre 1215 y 5 de una PG. es:
términos, siendo el primero 1 y el
B) 500, 100, 20,10 b) 10, 50, 150,
último 2048?
750
a) 1 b) 2 c) 4
C) 405, 135, 45, 15 d) 625, 250, 125, 25
d) 8 e) 16
26. En una PG. creciente de tres términos
se multiplica el primer término por 4, al
37. La suma de los 6 primeros términos de
una P.G. es igual a nueve veces a suma
segundo por 7 y al tercero por 6,
de los 3 primeros términos entonces la
obteniéndose una PA. Hallar la razón de
razón de la PG. es:
la PG.
a) 2 b) 3 c) 4 d) 7 e) 8
a) 2 b) 3 c) 4 d)5
27. Si el producto de tres números que 38. Si le sumamos 3 números consecutivos
están en P.G. es 1000 y la razón es 3. a 3, 7 y 16 respectivamente, obtenemos
¿Cúal de los sgtes no pertenece a P.G.? una P.G. calcular la razón de la P.G.
a)10/3 b)10 c) 30 d) 3 a) 1 b) 2 c) 3 d) 4 e) 5
28. Determinar el término central de una
PG. de 5 términos, Sabiendo que el 1 1 1
39. Sumar: + + + ...
producto de todos ellos es 1024 3 12 48
a) 3 b) 4 c) 5 d)6 a) 1 b) 2 c) 1/2
29. La suma de tres números en PA. es d) 1/4 e) 4/9
22,5. Si al centro se le resta 1,5 se

11. Ecuación Segundo Año
40. La suma de tres números en progresión Hallar el segundo término de la progresión
geométrica creciente es 70; si los extremos se geométrica dada.
multiplican por 4 y el intermedio por 5, los a) 15 b) 10 c) 30
productos están en progresión aritmética. d) 20 e) 18
Prof.: Rodolfo Angel Carrillo Velásquez
11

12. Tema nº 02 : funcioneS
Capacidades:
 Define y grafica funciones.
 Resuelve problemas con funciones.
Desarrollo del Tema:
PAR ORDENADO R: A → B
Es un conjunto que consta de 2 elementos al subconjunto de A × B obtenido mediante:
dispuestos en un determinado orden.
R = {(a ;b ) ∈ A × B /a ∈ A ∧ b ∈ B ∧ a R b }
( A ; B )
P r im e ra Segunda
a R b Indica que entre a ∈ A y b ∈ B se cumple
c o m p o n e n te c o m p o n e n te
alguna condición establecida.
Propiedades: • Ejemplo: Dado A = {1, 2, 3, 4} y B = {5, 6}
1. (A;B) ≠ (B;A) Construir una relación de A en B, definida por:
2. Si: (A;B) = (C;D) → A = C ∧ B = D R = {(a;b) ∈ A × B/a + b < 9}
• Ejemplo: Resolución:
Hallar (x + y), si se sabe que: * Obteniendo A × B:
(4x - 1;13) = (7; 2y - 1) A × B = {(1;5),(1;6),(2;5),(2;6),(3;5),(3;6),(4;5),(4;6)}
Resolución: Igualando las componentes: * Analizando cada par ordenado:
* 4x - 1 = 7 →x=2 (1;5) → 1 + 5 = 6 < 9 (cumple)
* 2y - 1 = 13 →y=7 (1;6) → 1 + 6 = 7 < 9 (cumple)
∴x+y=9 (2;5) → 2 + 5 = 7 < 9 (cumple)
(2;6) → 2 + 6 = 8 < 9 (cumple)
PRODUCTO CARTESIANO (3;5) → 3 + 5 = 8 < 9 (cumple)
Dados 2 conjuntos "A" y "B" no vacíos; se llama
(3;6) → 3 + 6 = 9 = 9 (no cumple)
"producto cartesiano de A y B" (A × B) al
conjunto de pares ordenados obtenido mediante: (4;5) → 4 + 5 = 9 = 9 (no cumple)
(4;6) → 4 + 6 = 10 > 9 (no cumple)
A × B = { (a ;b )/a ∈ A ∧ b ∈ B } ∴ R = {(1;5),(1;6),(2;5),(2;6),(3;5)}
• Ejemplo: Del ejemplo anterior podemos establecer:
Siendo: A = {3; 4; 5} 1. Como R es una relación de A en B, entonces:
B = {1; 2} * A: conjunto de partida de la relación.
A × B = { ( 3 ; 1 ) ,( 3 ;2 ) ,( 4 ; 1 ) ,(4 ; 2 ) ,( 5 ; 1 ) ,( 5 ;2 ) } * B: conjunto de llegada de la relación.
B × A = { ( 1 ; 3 ) ,( 1 ;4 ) ,( 1 ; 5 ) ,(2 ; 3 ) ,( 2 ; 4 ) ,( 2 ;5 ) }
2. Dominio de R: Dom(R) = {1; 2; 3}
Propiedades: (Conjunto de las primeras componentes)
1. A × B ≠ B × A (observar ejemplo anterior)
2. Siendo n(A) = número de elementos del 3. Rango de R: Ran(R) = {5;6}
conjunto A, (Conjunto de las segundas
→ n(A × B) = n(A) . n(B)
componentes)
RELACIÓN BINARIA
Dados 2 conjuntos "A" y "B" no vacíos; se define
"relación binaria de A en B":

13. Funciones Cuarto Año
Ejemplos:
1. En la siguiente igualdad de pares ordenados: Resolución: Obteniendo cada conjunto.
(2a +3b;-1) = (4;3a + b) A = {2; 3; 4}
Calcular el valor de "a + b" B = {2; 3; 4}
Resolución: Luego:
Por igualdad de pares ordenados se debe A×B=
cumplir: {(2;2),(2;3);(2;4),(3;2),(3;3),(3;4),(4;2), (4;3),(4;4)}
2a + 3b = 4.......... 1)
....( Graficando:
 B
3a + b = −1.......... 2)
....(
4
Resolviendo:
(1 ) × 3 : 6a + 9b = 12 A × B
3
(2 ) x -2 : -6 a - 2 b = 2
2
7b = 14
b = 2 1
A
E n (1 ): a = -1
0 1 2 3 4
piden : a + b = 1
b. A = {x ∈ IN /3 < x + 2 ≤ 5}
B = {x ∈ IR / |x - 4| ≤ 1}
2. Sea A = {1; 2; 3} y dadas las relaciones: R y Resolución: Obteniendo cada conjunto.
1
R en "A" definida por: A = {2; 3}
2 B = [3; 5]
R = {(x;y) ∈ A × A/x < y} El conjunto "A" posee sólo 2 elementos; en
1
R = {(x;y) ∈ A × A/x + y = 5} cambio el conjunto "B" está dado por un
2 intervalo.
Calcule el número de elementos de R ∪ R
1 2
Resolución: Graficando:
B
Para determinar: R y R debemos construir el
1 2
producto cartesiano así: 5
A×A=
E le m e n t o s
{(1;1),(1;2),(1;3),(2;1),(2;2),(2;3),(3;1), (3;2),
de "B"
(3;3)} 3
Luego:
* Los elementos de R son todos aquellas
1 A
(x;y) donde x < y: R = {(1;2),(1;3),(2;3)} 0 1 2 3 4 5
1
* Los elementos de R son todos aquellos
2 E le m e n t o s
(x;y) donde x + y = 5: R = {(2;3),(3;2)} de "A "
2
Finalmente, el conjunto R ∪ R , viene a ser: c. A = {x ∈ IR/3 < x ≤ 6}
1 2
R ∪ R = {(1;2),(1;3),(2;3),(2;3),(3;2)} ó B = {x ∈ IR/1 ≤ x < 5}
1 2
R ∪ R = {(1;2),(1;3),(2;3),(3;2)} Resolución: Los dos conjuntos están dados por
1 2
∴ n(R ∪ R ) = 4 intervalos.
1 2 Graficando en el plano cartesiano.
3. En cada caso, se dan 2 conjuntos "A" y "B",
calcular:
"A × B" y graficarlos sobre el plano cartesiano.
a. A = {x ∈ IN / |x - 3| < 2}
x+2
1< ≤2
B = {x ∈ IN / 3 }

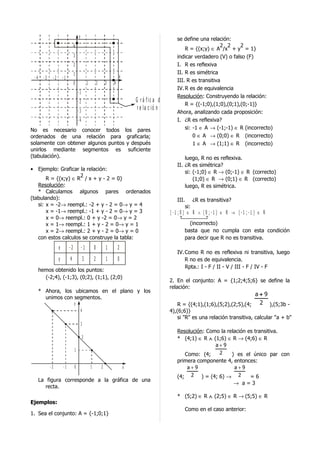
14. B Resolución:
5 * Construyendo la relación: 2x - y = 3
4
si: x = 1 → reemp.: 2(1) - y = 3
3 E le m e n t o s
de "B" → y = -1 ∉ M
2
1
x=2 → reemp.: 2(2) - y = 3
A → y=1∈M
0 1 2 3 4 5 6
E le m e n t o s d e " A " Luego (2;1) ∈ R
El rectángulo sombreado contiene todos los
pares ordenados (x;y) ∈ A × B. Las líneas x=3 → reemp.: 2(3) - y = 3
punteadas del rectángulo indican que en dicha → y=3∈M
parte de la gráfica el intervalo es abierto (A:
<3;6]; B: [1;5>) Luego (3;3) ∈ R
En el caso que la línea sea contínua, el
extremo del intervalo correspondiente es x=4 → reemp.: 2(4) - y = 3
cerrado. y=5∉M
4. Sea: M = {1; 2; 3; 4} un conjunto sobre el Se concluye que: R = {(2;1); (3;3)}
cual se define la relación: Dom(R) = {2;3} → a = 2 + 3 = 5
R = {(x,y)/2x - y = 3} Ran(r) = {1;3} → b = 1 + 3 = 4
Si "a" representa la suma de todos los elementos ∴a-b=1
del dominio de R y "b" a la suma de todos los
elementos del rango de R, calcular (a - b)
problemaS para la claSe
Bloque I Calcular: n(R)
a) 1 b) 2 c) 3
1. A partir de la igualdad: d) 4 e) 5
(a + b; 3a - 5) = (5; 4)
Hallar "2b - a" 6. Dados los conjuntos:
a) 1 b) 2 c) 3 A = {x ∈ IN/2 < x - 1 < 7}
d) 4 e) 5 B = {x ∈ IN/|x - 5| = 2}
Calcular: n(A × B)
2. Dada la operación: a) 7 b) 4 c) 8
(3x - 1;4) + (2x + 1;y + 2) = (y + 1;10) d) 6 e) 5
Hallar "x + y"
a) 1 b) 3 c) 5 7. Si: A = {1; 2; 3} ∧ B = {2; 4; 6}
d) 7 e) 9 Expresar por extensión la relación R; de "A" en
"B" definida así: R = {(x;y) ∈ A × B/y = 2x}
3. Teniendo lo siguiente: a) R = {(1;2),(2;4)}
(x + 1;y) + (3x - 1; 6) = (12;x + 7) b) R = {(1;1),(2;4),(3;5)}
Calcular "x + y" c) R = {(2;4),(1;6)}
a) 1 b) 3 c) 5 d) R = {(1;2),(2;4),(3;6)}
d) 7 e) 9 e) R = {(1;2),(2;4),(4;8)}
4. A partir de los conjuntos: 8. Dados los conjuntos:
A = {1; 2; 5; 6} A = {x ∈ IR/3 ≤ x + 1 ≤ 4}
B = {3; 5; 7} B = {x ∈ IR/0 ≤ x - 2 ≤ 2}
Construir la relación "R" definida por: Hallar "A × B", "B × A" y graficar cada caso:
R = {(x;y) ∈ A × B/x + y = 8}
9. Determinar los pares ordenados (x; y) que
5. Dado el conjunto: A = {2; 3; 4}, se define una 2
verifican la igualdad: (x ; x + y) = (y; 2)
relación "R", mediante:
a) {(-2; 1), (4; 1)} b) {(1; -2), (1; 4)}
2
R = {(x;y) ∈ A /x + y = 3º} c) {(-3; 1), (4; 2)} d) {(-2; 4), (1; 1)}

15. Funciones Cuarto Año
e) {(4; -2), (1; 1)} Indicar cuál de todos los pares ordenados
dados, no pertenecen al conjunto A × B; ni al
10.De la gráfica: conjunto B × A.
y a) (1; 6) b) (5; 4) c) (4; 4)
(8 ;1 1 ) d) (1; 7) e) (2; 5)
7. Sean los conjuntos:
A = {x ∈ ZZ /-1 ≤ x < 5}
(a + b ;5 ) B = {x ∈ ZZ / 2 ≤ x ≤ 4} y las
(1 2 ;a + 2 ) correspondencias:
R = {(x;y) ∈ A × B/x < y}
1
R = {(x;y) ∈ A × B/x + y = 3}
2
x
Hallar el número de elementos de:
Hallar "ab" Dom (R ) ∧ Ran (R )
1 2
a) 5 b) 10 c) 15
a) 0 b) 1 c) 2
d) 20 e) 25
d) 3 e) 4
Bloque II
8. Dados:
1. Dados los conjuntos:
A = {x ∈ IN / x = impar ∧ 3 < x < 11}
A = {x ∈ ZZ /|x - 1| ≤ 1}
3
2 B = {x ∈ IN / x ≤ 100 ∧ x = 12}
B = {x ∈ ZZ /x = 5x}
Cuáles de las relaciones:
Hallar "A × B", "B × A" y graficar cada caso.
I. R = {(9;2),(5;4),(7;3)}
1
2. Dados los conjuntos: II. R = {(3;1),(5;2),(7;3),(9;4)}
2
III. R = {(5;12),(7;4)}
A = {x ∈ ZZ /|x| < 2} 3
x +1 están definidas de "A" en "B"
a) Sólo I b) Sólo II c) Sólo III
B = {x ∈ ZZ /-1 < 3
< 0} d) I y III e) II y III
Hallar "A × B" y "B × A", graficar en cada
caso: 9. Si: A = {1; 2; 3; 4; 5}
Se define la relación:
3. Dados los conjuntos: R = {(1;1),(2;2),(3;3),(5;1),(2;4),(5;4),(5;2),
P = {x ∈ IR /4 ≤ 3x - 2 ≤ 7} (4;3),(3;5)}
Q = {x ∈ IR /0 ≤ x - 2 ≤ 1} Si: M = {x ∈ A/(x;2) ∈ R}
Hallar "P × Q" y "Q × P", graficar en cada N = {y ∈ A/(3;y) ∈ R}
caso: P = {x ∈ A/(x;5) ∈ R}
Entonces (M ∪ N) - P es:
4. Dados los conjuntos: a) {2;5} b) {3;5} c) {3}
A = {x ∈ IN /|x - 6| = 5} d) {5} e) {1;2;4;5}
x −1
10.Dados los conjuntos:
B = {x ∈ IN /1 < 2 < 3} A = {1; 2; 3; 4; 5; 6}
Hallar: n(B × A) B = {1; 3; 5}
a) 1 b) 6 c) 4 C = {2; 4; 6}
d) 8 e) 5 y las correspondencias:
P = {(x;y) ∈ B × A/x + y es par}
2 2 2 Q = {(x;y) ∈ C × B/x + y es impar}
5. Si: A = {-1; 0; 1} y R = {(x;y) ∈ A /y = x }
Hallar el número de elementos de "P v Q" si
Hallar: n(R)
existe.
a) 5 b) 4 c) 3
a) 15 b) 18 c) 21
d) 2 e) 1
d) 27 e) 30
6. Dados los conjuntos:
Bloque III
+
A = {x ∈ ZZ /|x - 1| < 4} 2
1. Dados los conjuntos: F = {x ∈ ZZ /x + 5 =
3x − 1 6x}
B = {x ∈ ZZ /2 < 4 < 5} 2
G = {x ∈ IR / x + 8 ≤ 6x}

16. entonces: F × G, tiene la forma:
6. Dados los conjuntos:
a) b) c) A = {1;4} ∪ {x ∈ IR /2 ≤ x ≤ 3}
B = {x ∈ IR / 5 ≤ x ≤ 7}
d) e) entonces A × B tiene la forma:
2. Dados los conjuntos: a) b) c)
A = {1;5} ∪ {x ∈ IR /2 ≤ x ≤ 4} d) e)
B = {x ∈ IR / 2 ≤ x ≤ 3} 7. Si: A = {x ∈ ZZ /4 < x + 4 < 9}
entonces "A × B", tiene la forma: 3 2
B = {x ∈ IR / x - 5x - x + 5 = 0}
a) b) c) Definimos: R = {(x;y) ∈ A × B/x < y}
Hallar la suma de los elementos que
conforman el dominio de la relación "R".
d) e) a) 6 b) 7 c) 9
d) 10 e) 11
3. Si "A" y "B" son los conjuntos definidos por:
A = {x ∈ IR / 3 ≤ x ≤ 6} 2
B = {y ∈ IR / -1 ≤ y ≤ 4} 8. Sean los conjuntos: A = {x ∈ IR / |x| ≤ 1}
Entonces, el área de la región limitada por el B = {x ∈ IR / 6 ≤ 3x ≤ 12}
gráfico de A × B, es: indicar la gráfica aproximada de A × B
2
a) 10u b) 15 c) 20
d) 12 e) 18 a) b) c)
4. Dados los pares ordenados:
P = (2; 3a - b); Q = (-5; 7); R = (a - 3b; -1) d) e)
cuya representación en el plano cartesiano
genera tres puntos. Los puntos "P" y "Q" están 9. Dados los conjuntos:
sobre una misma recta horizontal, mientras 2
M = {x ∈ IN / (x - 2)(x - 3) = (x - 2)2x}
que "Q" y "R" sobre una misma recta vertical. 2
Luego "a + b" es igual a: N = {x ∈ IR / x ≤ |x| + 2}
a) 3 b) -3 c) 2 Indicar lo incorrecto:
d) -2 e) 6 a) (2; 0) ∈ M × N b) (3; 1) ∈ M × N
5
( ; 0)
5. La gráfica del conjunto: A={1; 2};× ∈ <1; 2> es: c) (0; 3) ∈ N × M d) 2 ∈M×N
2 2
e) (3; -2) ∈ M × N
1 1
10.En el conjunto A = {1; 2; 3; 4; 5} se define una
a) 1 2 b) 1 2 2 2
relación "R" por: R = {(x;y) ∈ A / x - 2 ≤ y}
2
2
Si: m = suma de elementos del dominio de R.
1 1 n = suma de elementos del rango de R
c) 1 2 d) 1 2 Hallar "m + n"
2
a) 16 b) 18 c) 20
d) 22 e) 24
1
e) 1 2
Tarea Domiciliaria
1. Dada la igualdad: sabiendo que:
(4x - 3; 5x + 2y) = (1;11) A = {1; 2; 3}
Hallar "x + y" B = {2; 4; 5}
2 e indicar el número de elementos de "R"
2. Sabiendo que: (a ;a + 1) = (9;-2)
Hallar "a"
4. Si: A = {x/x ∈ IN ∧ 1 < x < 4}
B = {x/x ∈ IN ∧ 3 ≤ x ≤ 5}
3. Construir la relación "R", donde:
R = {(x; y) ∈ A × B/x + y > 6} Indicar un par ordenado de A × B
5. Si: P = {y/y ∈ IN ; y = 3x + 1 ∧ 2 < x < 7}

17. Funciones Cuarto Año
N = {x/x ∈ ZZ ; x = y -3 ∧ -1 ≤ y ≤ 1} 17.Realizar la gráfica de la relación:
Indicar: n(P × N) 2
R = {(x;y) ∈ R /x ∈ [-2;5>; y ∈ [-1;4]}
3
6. Si: A = {1;2}; B = {1;2}
18.Realizar la gráfica de la relación:
Hallar: M = {(x;y) ∈ A × B/y = 2x}
2
R = {(x;y) ∈ R / x ∈ [-3;5>; y ∈ [-2;4]}
2
7. Si: A = {x ∈ IN / "x" es impar ∧ 7 ≤ x ≤ 12} 19.Sean los conjuntos:
B = {x ∈ IN / "x" es par ∧ 5 < x < 11} A = {1;2;3;4;5;6}
determinar: R = {(x;y) ∈ A × B/x + y = 15} B = {1;4;9;16;25;36;49}
dar como resultado n(R) 2
R = {(x;y) ∈ A x B/y = (2x + 1) }
Halle su dominio y su rango.
8. Si: P = {x ∈ IN /5 < x + 5 < 10}
2 20.Sean las relaciones:
Q = {x ∈ IR /x - 4 = 0}
Definimos la relación: R = {(x; y) ∈ P × Q/x > y} 2
R = {(x;y)/y = x - 1, x ∈ {1;2;3;4}}
Hallar la suma de los elementos que S = {(x;y)/y = 2x + 1, x ∈ {1;2;3;4}}
conforman el rango de la relación. Halle: n(Dom(R)) + n(Ran(S))
9. Dados los conjuntos: 21.Determinar los pares ordenados (x;y) que
2 2
M = {x ∈ ZZ /x + 2 = 38} verifican la igualdad: (x ; x + y) = (y;2)
2
N = {x ∈ IR / x + 8 ≤ 6x}
22.Si: A = {1;2;3;4;5}
Entonces, M × N, tiene la forma:
R ∧R ⊂A×A
1 2
10.Dados los conjuntos: R = {(x;y)/x < y}
1
A = {2;4} ∪ {x ∈ IR /3 ≤ x ≤ 7/2 }
R = {(x;y)/x + y = 6}; Hallar: Dom(R ∩ R )
B = {x ∈ IR /3 ≤ x ≤ 5} 2 1 2
Entonces: A × B; tiene la forma:
23.Dados los conjuntos:
11.Si: A = {x ∈ IN / "x" es impar; x ∈ ]1;8[} P = {x ∈ IN /1 < x < 4}
Q = {x ∈ IN /1 ≤ x ≤ 4}
B = {x ∈ IN / "x" es par; x ∈ [4;10]}
de las afirmaciones:
Determinar: V = {(x;y) ∈ A x B/x + y < 12}
I. (1;1) ∈ P × Q
II. (2;1) ∈ Q × P
12.Del siguiente enunciado: III.(3;3) ∈ P × Q
S = {(2; 3), (1; 5), (2; 4),(1; 7)} ¿Cuáles son verdaderas?
Determinar el dominio de "S"
24.Dados los conjuntos:
13.Si: A = {1;2;3}; B = {2;5} A = {3;5;7}; B = {2;4;6}
M = {(x;y) ∈ A × B/x + y ≤ 5} se definen las relaciones:
R = {(x;y) ∈ A × B/x + y = 9}
Determinar el n(M) 1
R = {(x;y) ∈ A × B/y = 4}
2
14.Sea: A = {1;2;3;4;5} y las relaciones en "A" Hallar: Dom(R - R )
F = {(x;y) ∈ A x A/x < y} 1 2
G = {(x;y) ∈ A x A/x + y = 5}
25.De B = {1;2;3;4} y las relaciones:
¿Cuántos elementos tiene F ∪ G?
R = {(x;y) ∈ B × B/y = x}
1
15.R es una relación en A = {2; 3; 9} definida R = {(x;y) ∈ B × B/y < x}
2
2 R = {(x;y) ∈ B x B/x < y}
por: R = {(x;y)/y + 1 ≤ x }; hallar: n(R) 3
Hallar: n(R ) + n(R ) - n(R )
3 2 1
16.Sabiendo que:
A = {x ∈ IN/4 < x < 7} ; B = {-1; 0; 1}
26.De A = {x ∈ IN/x ≤ 9} y definimos:
Indicar lo correcto: 2
a) (-1; 0) ∈ A × B b) 7 ∈ A R = {(x,y) ∈ A /y = x}
c) (4; 7) ∈ A × B d) (5; 0) ∈ A × B e) 0 ∈ A 2
T = {(x,y) ∈ A /x < 4 ∧ y > 7}

18. 2 R = {(x;y) ∈ Z × Z/y = ax + b}
S = {(x,y) ∈ A /y = 2x}
Hallar el valor de "a + b"
Hallar: n(R) + n(S) + n(T)
29.Graficar: R = {(x;y)/y = 2x + 1, x ∈ A} donde:
27.Traza la gráfica de la relación:
A = {-1; 0; 2; 3}
2
R = {(x;y) ∈ R /x ∈ <-1;5>; y ∈ <-2;4>}
2
30.Traza la gráfica de la siguiente relación:
R = {(x;y) ∈ R × R/5x - 3y + 7 = 0; x ∈ <-2;4]}
28.Si los pares ordenados (2n;0), (0;-n) y (n;1) 1
pertenecen a la relación:
CLASES DE RELACIONES 2. La relación:
Sabemos que, a partir de un conjunto "A", se "x es hermano de y"
puede definir una relación "R" en "A", es decir: también es simétrica, puesto que:
R∈A×A "Alberto es hermano de José"
Expresar mediante: entonces:
R = {(x;y) ∈ A × A/x Ry} "José es hermano de Alberto"
donde "x R y" indica la condición que debe
cumplirse para que el par ordenado (x;y) ∈ R.
C. "R" es transitiva, si se cumple:
• Ejemplo: (x ;y ) ∈ R ∧ (y ;z ) ∈ R → (x ;z ) ∈ R
Dado: A = {2;3;4;5;6;7}, el conjunto
R = {(x;y) A × A/x + y = 9} Ejemplos:
es una relación en A, cuyos elementos son: 1. Dado el conjunto A = {2;4;6}
(2;7), (3;6), (4;5), (5;4), (6;3), (7;2) se define la relación:
Siendo "R" una relación de "A" en "A" (relación en R = {(2;2),(2;4),(4;4),(6;6),(4;2)}
A), se puede realizar la siguiente clasificación:
si:
A. "R" es reflexiva, si cumple: (2 ;2 ) ∈ R ∧ (2 ;4 ) ∈ R → (2 ;4 ) ∈ R
∀ x ∈ A → (x ;x ) ∈ R (correcto)
es decir, cualquier elemento del conjunto "A",
(2 ;4 ) ∈ R ∧ (4 ;4 ) ∈ R → (2 ;4 ) ∈ R
se relaciona consigo mismo mediante la (Correcto)
relación "R" (4 ;4 ) ∈ R ∧ (4 ;2 ) ∈ R → (4 ;2 ) ∈ R
Ejemplo: Dado el conjunto: A = {2; 3; 4}
se define: (Correcto)
R = {(2;2), (2;3), (2;4), (3;3), (3;4)} (2 ;4 ) ∈ R ∧ (4 ;2 ) ∈ R → (2 ;2 ) ∈ R
si: 2 ∈ A → (2;2) ∈ R (correcto)
(Correcto)
3∈A → (3;3) ∈ R (correcto)
∴ R es transitiva.
4∈A → (4;4) ∈ R (correcto)
∴ R es reflexiva.
2. La relación entre conjuntos:
x ⊂ y ("x" está incluido en "y")
B. "R" es simétrica, si cumple:
es transitiva, puesto que:
(x ;y ) ∈ R → (y ;x ) ∈ R A ⊂ B ∧ B ⊂ C → A ⊂ C
Ejemplos:
En forma gráfica:
1. Dado el conjunto: A = {4; 7; 9}
U
se define la relación:
R = {(4;7), (7;9), (7;4), (9;7), (4;4)} C
B
si: (4;7) ∈ R → (7;4) ∈ R (correcto) A
(7;9) ∈ R → (9;7) ∈ R (correcto)
(4;4) ∈ R → (4;4) ∈ R (correcto)
∴ R es simétrica.

19. Funciones Cuarto Año
D. "R" es una relación de equivalencia, si es Este conjunto de pares ordenados conforma el
reflexiva, simétrica y transitiva a la vez. plano cartesiano:
Ejemplos:
y
1. Con el conjunto A = {1; 3; 5}
analicemos la relación definida en "A" P (a ;b )
R = {(1;1),(3;3),(5;5),(1;3),(3;1)} II I
veamos si "R" es reflexiva
si: 1 ∈ A →(1;1)∈R 0 x
(1 ;1 ) ∈ R ∧ (1 ;3 ) ∈ R → (1 ;3 ) ∈ R
(correcto)
III IV
3 ∈ A → (3;3) ∈ R
(3 ;3 ) ∈ R ∧ (3 ;1 ) ∈ R → (3 ;1 ) ∈ R
(correcto) donde: eje x: eje de abscisas
eje y: eje de ordenadas
5 ∈ A → (5;5) ∈ R 0: origen de coordenadas
(1 ;3 ) ∈ R ∧ (3 ;1 ) ∈ R → (1 ;1 ) ∈ R I, II, III, IV: cuadrantes
(correcto)
luego, R es reflexiva.
Cada par ordenado (a;b) del conjunto R , se
2
Veamos si "R" es simétrica puede representar en el plano mediante un punto
si: (1;1) ∈ R → (1;1) ∈ R (correcto) P, donde:
(1;3) ∈ R → (3;1) ∈ R (correcto) a: coordenada de "P" en el eje "x"
(5;5) ∈ R → (5;5) ∈ R (correcto) b: coordenada de "P" en el eje "y"
Entonces, si definimos una relación "R",
luego "R" es transitiva mediante:
2
R = {(x;y) ∈ R /x R y}
como la relación "R" es reflexiva, simétrica
y transitiva a la vez Se dice que la gráfica de la relación R es un
∴ R es de equivalencia
conjunto de puntos representados en el plano
cartesiano, cuyas coordenadas satisfacen dicha
2. La relación de igualdad:
relación.
R = {(x;y)/x = y}
es reflexiva, pues ∴∀ x → (x,x) ∈ R
• Ejemplo: A partir del conjunto A = {-2; 0; 4}
es simétrica, pues (x;y) ∈ R→ x = y
graficar la relación R, dada por:
→y=x
→ (y;x) ∈ R R = {(x;y) ∈ A × A/x + y > 0}
Resolución:
es transitiva, pues * Construyendo la relación:
( x ,y ) ∈ R ∧ ( y ; z ) ∈ R R = {(-2;4),(0;4),(4;-2),(4;0),(4;4)}
→x=y∧y=z * Los 5 pares representan 5 puntos que se
→x=z ubican en el plano:
→ (x;z) ∈ R
∴ R es relación de equivalencia.
GRÁFICA DE RELACIONES
Se sabe que el producto cartesiano de 2
conjuntos "A" y "B", está dado por:
A × B = {(x;y)/x ∈ A ∧ y ∈ B}
si hacemos: A = B = R (conjunto de número
reales) se tiene el conjunto.
2
R × R = R = {(x;y)/x ∈ R ∧ y = R}

20. y
se define una relación:
4 2 2 2
R = {(x;y) ∈ A /x + y = 1}
3 indicar verdadero (V) o falso (F)
2 I. R es reflexiva
1 II. R es simétrica
-4 -3 -2 -1 x
0 1 2 3 4 III. R es transitiva
IV. R es de equivalencia
-1
Resolución: Construyendo la relación:
-2 G r á f ic a d e la
R = {(-1;0),(1;0),(0;1),(0;-1)}
-3
r e la c ió n " R "
Ahora, analizando cada proposición:
-4 I. ¿R es reflexiva?
No es necesario conocer todos los pares si: -1 ∈ A → (-1;-1) ∈ R (incorrecto)
ordenados de una relación para graficarla; 0 ∈ A → (0;0) ∈ R (incorrecto)
solamente con obtener algunos puntos y después 1 ∈ A → (1;1) ∈ R (incorrecto)
unirlos mediante segmentos es suficiente
(tabulación). luego, R no es reflexiva.
II. ¿R es simétrica?
• Ejemplo: Graficar la relación:
si: (-1;0) ∈ R → (0;-1) ∈ R (correcto)
2
R = {(x;y) ∈ R / x + y - 2 = 0} (1;0) ∈ R → (0;1) ∈ R (correcto)
Resolución: luego, R es simétrica.
* Calculamos algunos pares ordenados
(tabulando): III. ¿R es transitiva?
si: x = -2→ reempl.: -2 + y - 2 = 0→ y = 4 si:
x = -1→ reempl.: -1 + y - 2 = 0→ y = 3 (-1 ;0 ) ∈ R ∧ (0 ;-1 ) ∈ R → (-1 ;-1 ) ∈ R
x = 0→ reempl.: 0 + y -2 = 0→ y = 2
x = 1→ reempl.: 1 + y - 2 = 0→ y = 1 (incorrecto)
x = 2→ reempl.: 2 + y - 2 = 0→ y = 0 basta que no cumpla con esta condición
con estos calculos se construye la tabla: para decir que R no es transitiva.
x -2 -1 0 1 2
IV. Como R no es reflexiva ni transitiva, luego
y 4 3 2 1 0 R no es de equivalencia.
Rpta.: I - F / II - V / III - F / IV - F
hemos obtenido los puntos:
(-2;4), (-1;3), (0;2), (1;1), (2;0)
2. En el conjunto: A = {1;2;4;5;6} se define la
relación:
* Ahora, los ubicamos en el plano y los
a+9
unimos con segmentos.
y R = {(4;1),(1;6),(5;2),(2;5),(4; 2 ),(5;3b -
4 4),(6;6)}
si "R" es una relación transitiva, calcular "a + b"
3
Resolución: Como la relación es transitiva.
2 * (4;1) ∈ R ∧ (1;6) ∈ R → (4;6) ∈ R
a+9
1
Como: (4; 2 ) es el único par con
primera componente 4, entonces:
-2 -1 0 1 2 x a+9 a+9
(4; 2 ) = (4; 6) → 2 =6
La figura corresponde a la gráfica de una
→ a=3
recta.
* (5;2) ∈ R ∧ (2;5) ∈ R → (5;5) ∈ R
Ejemplos:
Como en el caso anterior:
1. Sea el conjunto: A = {-1;0;1}

21. Funciones Cuarto Año
(5; 3b - 4) = (5;5) → 3b - 4 = 5 obtenga la gráfica de dicha relación.
→ b=3
∴a+b=6 Resolución:
Dando diversos valores a "x" y calculando los
3. Se define la siguiente relación en Z: valores correspondientes a "y", obtenemos los
R = {(x ; y) ∈Z x Z / x ≤ y} pares de valores que figuran en la siguiente
La relación R es transitiva. tabla:
¿Verdadero o Falso?
Resolución: x 0 1 2 3 4 5 6 -1
Para que la relación "R" sea transitiva, debe y 0 8 6 0 -4 0 1 8 -2 4
cumplir lo siguiente:
(x ;y ) ∈ R ∧ (y ;z ) ∈ R → (x ;z ) ∈ R cada par de valores corresponde a un punto en
el plano. Al ubicarlos en el plano, se unen
veamos: mediante segmentos y tenemos la gráfica de la
considerando los pares ordenados: relación.
(x,y) ∈ R ∧ (y;z) ∈ R → (x;z) ∈ R
De la figura:
luego, estos elementos deben satisfacer la
condición dada:
20
x≤y∧y≤z→x≤z
→ (x;z) ∈ R 10
lo que queríamos comprobar: 0 3 5
∴ R es transitiva. -2 -2 1 2 4 6
4. Se define una relación en R mediante: -1 0
3 2
(x;y) ∈ R ↔ y = x - 8x + 15x -2 0
problemaS para la claSe
Bloque I a) 1 b) 2 c) 3
1. A partir del conjunto A = {3;4;5} d) 4 e) 5
Se definen las relaciones en A:
R = {(3;3),(4;3), (4;5), (5;5)} 4. Para el conjunto: A = {1;3;5}
1
Se define la relación reflexiva.
R = {(3;3),(3;5), (4;4), (5;4)}
2 R = {(1;a-2), (3;3), (5;b+3), (1;3), (3; a - b)}
R = {(3;3),(4;4), (5;3), (5;5)} Indicar verdadero (V) o falso (F).
3
Indicar cuáles son reflexivas. I. R es simétrica.
a) Sólo R b) R y R b) Sólo R II. R es transitiva.
1 1 2 3 III. R es de equivalencia.
d) Sólo R e) R y R a) VVF b) VFF c) FVV
2 2 3
d) FFF e) VVV
2. Dado el conjunto: A = {1; 2; 3; 4}
Se definen las relaciones siguientes: 5. Se define una relación simétrica S, de tal
R = {(1;1), (2;1), (1;2), (3;3)} forma que:
S = {(1;4), (4;1), (3;4), (4;3)} (4; 2) ∈ S → (2; 2a + b) ∈ S
T = {(2;4), (4;2), (3;2), (3;3)} (5; 1) ∈ S → (1; a + 2) ∈ S
¿Cuáles son simétricas? Hallar el valor de "b".
a) R b) S c) Todas a) 2 b) -3 c) -6
d) R y S e) R y T d) 3 e) -2
3. Se tiene la relación simétrica: 6. Sea T una relación transitiva tal que:
R = {(5; 7), (7; 2a + b), (1; 8), (3b - 1; 1)} (2; 9) ∈ T ∧ (9; m + 2) ∈ T → (2; 11) ∈ T
Definida sobre un conjunto "A". (5; 7) ∈ T ∧ (7; 9) ∈ T → (5; n+2) ∈ T
Calcular (a + b).

22. I. R es reflexiva.
Calcular: m+n II. R es simétrica.
a) 9 b) 7 c) 16 III. R es transitiva.
d) 2 e) 4 a) Sólo I b) I y II c) Sólo III
d) II y III e) Todas
7. La relación R = {(2;a+b), (4;5), (5b;9)}
Tiene por gráfica: 2
B 2. Si el par ordenado (a - 16; a+ 2) pertenece al
segundo cuadrante de un plano cartesiano,
9 calcular la suma de los valores enteros de "a"
que verifican esta condición.
6+b a) 3 b) 2 c) -1
d) 4 e) 5
5
3. Dada la siguiente gráfica.
y
0 A
2 4 a+ 4
Hallar "a . b". 3
a) 10 b) 12 c) 14
d) 16 e) 20 2
1
8. Dada la gráfica de una relación reflexiva en: -3 -2 -1
A = {1, 3, 4, 7} A 0 1 2 3 x
Calcular "m + n + p" (3 p -2 )
-1
a) 4 b) 5 4 -2
c) 6 d) 7
e) 8
(2 n -1 ) -3
m Indicar a qué relación corresponde:
0 A a) y = 2x b) y = 2x -1 c) y = 2x +1
9. Dada la gráfica de una relación R en 1A. 3 4 7
A d) y = x + 1 e) y = x - 1
5
4. Las siguientes relaciones:
3 R = {(a;b), (b;c), (a;c), (c;c)}
S = {(a;a), (b;b), (a;c), (a;b)}
T = {(a;a), (b;a), (c;c)}
1
Se definen a partir de A = {a; b; c}
A Indicar lo correcto.
0 1 3 5 a) R es transitiva
con A = {1;3;5}. Luego: b) S es transitiva
a) R es reflexiva b) R es simétrica c) T es transitiva
c) R es transitiva d) R es equivalencia d) Ninguna es transitiva
e) Todas e) R y S son transitivas
10.Con el conjunto: A = {1;3;4} 5. Con el conjunto A = {1; 2; 3}
Se define la relación: Se define la relación:
S = {(x;y) ∈ A x A / (x + y) es par} R = {(1;1), (2;2), (3;3), (1;2), (2;1)}
Indique lo correcto. Señale lo correcto.
a) S es reflexiva b) S es simétrica a) R no es reflexiva
c) S es transitiva d) S es equivalencia b) R no es simétrica
e) Todas c) R no es transitiva
d) R es de equivalencia
Bloque II e) Todas son correctas
1. En el conjunto A = {2; 3; 5; 6} 6. Graficar la relación en R:
Se considera la relación: 2
S = {(x;y) ∈ R / 2x - y + 1 = 0}
2
R = {(x;y) ∈ A / x = y ∨ x + y = 8 }
Podemos afirmar que:

23. Funciones Cuarto Año
7. Graficar mediante tabulación , la siguiente y y
2
relación: 3x - y = 0
x x
8. Sabiendo que x ≥ 0, graficar la relación
a) b)
2 2 y
mediante tabulación: x + y = 25 y
9. A partir del conjunto A = {2; 5; 6}
Se construyen las relaciones: x x
2 c) d)
R = {(x;y) ∈ A / x ≠ y} y
1
2
R = {(x;y) ∈ A / x + y es impar}
2
2 x
R = {(x;y) ∈ A / xy = 1º0}
3 e)
¿Cuáles son simétricas?
a) R b) R c) R y R 2 2 2
1 2 1 2 3. La gráfica de la relación x + y = r
d) R y R e) Todas corresponde a una circunferencia de centro "0"
1 3
y radio "r", tal como se muestra en la figura:
10.Dado el conjunto A = {1; 2; 3; 4}
y
Sobre el cual se definen las relaciones:
2
R = {(x;y) ∈ A / |x| = y}
1
2
R = {(x;y) ∈ A / y = x + 2}
2 -2 0 x
2
R = {(x;y) ∈ A / 3(4y + 8) = 4(3x + 6)}
3
Luego, serán reflexivas:
a) R b) R y R c) R y R
1 1 2 1 3
Si el área del triángulo sombreado es 3r,
d) R e) R y R
2 2 3 calcular "r".
a) 2 b) 5 c) 2 10
Bloque III
1. Graficar la relación: d) 15 e) 3 2
R = {(x;y) / 2x - 3y - 6 = 0; 1 < x ≤ 6 } 4. Se define la relación:
y 2
y R = {(x; y) ∈ R / (2a - b)x - 3y + b - 5 = 0}
Si: (1; 3) ∈ R, calcular el valor de "a".
a) 3 b) 5 c) 7
x x d) 9 e) 11
a) b)
y y
5. Dada la relación R definida por:
R = {(x;y) ∈ R x R / |x - y| ≤ 4}
Es cierto que:
x x a) R es reflexiva
b) R es simétrica
c) d)
y c) R es transitiva
d) R es de equivalencia
e) R no es equivalencia
x 6. Obtener el área de la figura formada por la
e) gráfica de la relación:
2
R = {(x;y) ∈ R / |x| + |y| = 2}
2. Graficar, mediante tabulación, la siguiente 2
a) 2µ b) c) 4
relación:
d) e) 8
3 2
y = x - 6x + 8x
7. Calcular el área que forma la gráfica de la
relación:

24. 2 y
R = {(x;y) ∈ R / |x - 5| = |y - 2|}
2
Con el eje de ordenadas. 2
2 x
a) 5µ b) 10 c) 15 -2
d) 20 e) 25 e)
8. Graficar la relación en R. 9. Se definen las siguientes relaciones en A =
R = {(x;y) / |x| = |y - 2|} {a;b;c;d}:
y y R = {(a;a),(a;b), (b;b), (b;c), (c;c), (a;c), (d;d)}
2
1
R = {(a;a),(a;b), (b;a), (b;c), (c;b), (c;c), (d;d)}
2
-2 2 x -2 x
R = {(a;a),(a;b), (b;b), (c;c), (c;d), (d;d)}
-2 -2 3
a) b)
y Si se tienen "m" relaciones reflexivas, "n"
y relaciones simétricas y "p" relaciones
2
transitivas, hallar "m + n + p".
x -2 2 x a) 9 b) 8 c) 7
d) 6 e) 5
c) d)
Tarea Domiciliara
1. A partir del conjunto A = {2;8;9} B
Se define la relación: 3
R = {(x;y) ∈ A x A / x - y = 0}
Indicar un elemento en R. 2
2. Dado el conjunto A = {3; 5; 7} y las relaciones 1
en A: R = {(3;3), (5;5), (7;7)}
S = {(3;5), (5;5), (5;7)}
T = {(3;7), (5;5), (7;7)}
0 1 2 3 A
Indica cuál o cuáles son reflexivas. Señale lo correcto:
a) (1;2)∉R b) (3;2)∉R c) (2;2)∉R
3. Sobre el conjunto A = {1; 4; 9} d) (3;1)∉R e) (1;1)∈R
Se definen las relaciones siguientes:
R = {(1;4), (4;1), (1;9)} 7. La relación: R = {(1;4), (2;2), (3;1)}
S = {(1;9), (4;9), (9;1)} Tiene la siguiente gráfica:
T = {(1;1), (4;9), (9;4)} B
¿Cuáles son simétricas? 4
4. Dado el conjunto A = {1; 3; 5; 7}
Sobre el cual se definen las relaciones: (b + 1 )
R = {(1;1), (3;3), (5;5), (7;7)}
(3 c-2 )
S = {(1;5), (3;3), (5;7), (1;7)}
T = {(7;5), (5;3), (7;3)} 0 (a -2 ) 2 3 A
¿Cuáles son transitivas?
Calcular: E = a + b + c
5. Sobre el conjunto: A = {2; 4; 6}
Se construye la relación S. 8. La siguiente gráfica:
S = {(2;2), (2;4), (4;4), (6;6), (4;2)}
¿Es de equivalencia? Justifique.
6. La gráfica de una cierta relación R : A → B
Está dada por:

25. Funciones Cuarto Año
y A
3
2 3
1
2
-3 -2 -1 0 1 2 3 x
1
-1
-2 0 1 2 3 A
-3 Donde A = {1; 2; 3}
Marque lo correcto.
¿A qué relación corresponde? a) R es reflexiva b) R es simétrica
c) R es transitiva d) R es de equivalencia
9. Graficar la relación: 2x - y - 4 = 0 e) Todas
y y y
4 2
16.Si el par ordenado (2 - x; x - 4) pertenece al
x -2 x 4 x tercer cuadrante de un plano cartesiano, ¿cuál
a) b) c) es el menor valor entero que verifica esta
y y
condición?
2
x x 17.Dada la relación:
.-4
d) e) R = {(x;y) ∈ R x R/ x - y + 3 = 0; x ∈ [-1;4>}
Bosquejar su gráfica.
2
10.Graficar la relación: x - y = 0
y y y
x x x a) b) c)
a) b) c)
y y
d) e)
x x
d) e)
18.Graficar la relación:
R = {(x;y) / |x| = |y|}
11.Dado el conjunto A = {4; 5; 6}
Se define la relación reflexiva: y y y
R = {(4; 2m), (5; n+3), (6; 3p)}
Calcular "m", "n" y "p". x x x
a) b) c)
12.Se tiene una relación simétrica R, tal que: y y
(3; 7) ∈ R → (7; 2a - 5) ∈ R
Calcular el valor de "a". x x
d) e)
13.Sea R una relación transitiva tal que:
(3; 5) ∈ R ∧ (5; x - 4) ∈ R → (3; 7) ∈ R
19.Graficar la relación:
Calcular "x".
2 2
R = {(x;y) R x R / (x - 2) + y = 4; x ≤ 2}
14.Con el conjunto A = {2; 4; 7}
Se define la relación:
T = {(x;y) ∈ A x A / x + y = 3º}
¿"T" es simétrica? Justifique.
a) b) c)
15.Dada la gráfica de una relación R en A:
d) e)
20.Graficar, mediante tabulación, la relación
establecida mediante:

26. 3 OH 2
y = x - 4x =
Hallar el área del triángulo OAB, si: HB 1
25.Se tiene dos relaciones definidas en el
a) b) c) conjunto:
A = {0; 1; 2; 3; 4; 5}
2
S = {(x;y) ∈ A / y = 2x + 5}
d) e) 2 2 2
T = {(x;y) ∈ A / x + y = 25}
21.En A = {1; 2; 4; 6; 8} se define la relación: Se puede afirmar acerca de la clase de
R = {(x;y) / 3 es divisor de "x + y"} relación:
¿R es reflexiva, simétrica y transitiva?
Justifique. 26.Mediante tabulaciones, graficar la relación:
2 2
22.Dado el conjunto: A = {2; 4; 7} x - 2x + y - 3 = 0 , con x ≥ 0
y y y
Se define la relación reflexiva.
R = {(2; a - 1), (4; 2a - b), (7; b + c)}
Calcular el valor de: a + b - c x x x
a) b) c)
23.Graficar la relación: y
y
|x| + |y| = 4
x x
d) e)
a) b) c)
27.Dada la relación en R.
S = {(x;y) / - 1 < x - y < 2}
¿Es reflexiva?
d) e)
28.Graficar la relación definida en R
24.A partir de la figura: 2 2
y x - 4x + y - 10y + 13 = 0
A
a) b) c)
0 H B x
x = -y 2 + 9 d) e)

27. Funciones Cuarto Año
función:
Dados 2 conjuntos "A" y "B" no vacíos; se define FUNCIÓN DE "A" EN "B":
F:A→B
A la relación de A en B que cumple:
"A un elemento del conjunto "A" le corresponde un único elemento del conjunto B".
* Ejemplos:
F
A B
x y
c o n ju n to d e c o n ju n to d e
p a r t id a lle g a d a
F G
A B A B
1 4 3 2
2 3 5 4
4 0 6 1
F = {(1;4), (2;3), (4;0)} G = {(3;2), (3;4), (6;1)}
Si es función No es función
(cumple definición) (No cumple definición)
Pues al elemento 3 de A le
corresponde 2 elementos de B.
Observaciones: * (2; a) ∈ F ^ (2;5) ∈ F → a = 5
* (3; b + 1) ∈ F ^ (3; 6) ∈ F → b + 1 = 6
1. (x;y) ∈ F → y = F(x), donde: b=5
x : pre - imagen de y ∴ a + b = 10
y : imagen de x mediante F.
Ejemplo: De la función: F = {(4;1), (6;2), (3;7)} 3. DOMINIO DE UNA FUNCIÓN
(4; 1) ∈ F → F(4) = 1 Conjunto de pre - imágenes
(6; 2) ∈ F → F(6) = 2 RANGO DE UNA FUNCIÓN
(3; 7) ∈ F → F(3) = 7 Conjunto de imágenes
Ejemplo: De la función:
2. (a;b) ∈ F y (a;c) ∈ F → b = c F = {(4;1), (6;2), (3;7)}
Ejemplo: Dominio de F = Dom(F) = {4; 6; 3}
Si F = {(2; a), (3; b + 1), (2;5), (3; 6), (7; 2a - 1)} Rango de F = Ran(F) = {1; 2; 7}
Es función, calcular "a + b"
Resolución:

28. 4. y = F(x) se le llama Regla de Sea "F" una función real (F : R → R) La gráfica
correspondencia de F. de F es el conjunto de todos los puntos en el
Ejemplo: Dado F(x) = 2x + 1, plano cartesiano obtenido mediante:
con Dom(F) = {4, 6, 0}
* x = 4 → F(4) = 2(4) + 1 = 9 G = {(x,y) ∈ R x R / x ∈ Dom (F) ^ y = F(x)}
* x = 6 → F(6) = 2(6) + 1 = 13
* x = 0 → F(0) = 2(0) + 1 = 1 "Una relación F ⊂ R x R es una función real si
Luego: F = {(4;9), (6;13), (0;1)} y solamente si las rectas paralelas al eje "y",
que cortan a la gráfica de F, lo hacen a lo más
GRÁFICA DE UNA FUNCIÓN en un punto".
y y
G
F
1 p u n to 2 p u n to s
x x
F es función, pues la recta paralela al eje "y" trazada, G no es función, pues la recta
paralela al eje "y" trazada,
corta a su gráfica en un sólo punto. corta a su gráfica en más de 1 punto.
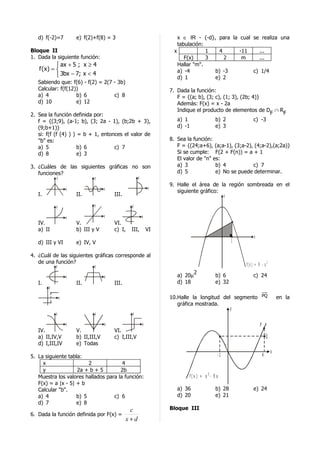
Ejemplos: 2
F(x) = ax + b
x 1 0
1. Si la relación:
F(x) 8 5
2
F = {(a;5), (2; a - 3a), (4; a), (2; 2a - 6), Luego, el producto "a.b" es:
(4; b - 1)} Resolución: de la tabla
Es una función, entonces el valor de: * Si: x = 1 → F =8
(1)
F(b) + F[F(a) - 3] será:
2
Resolución: Luego: F = a(1) + b → a + b = 8 ....... (1)
(1)
* Por ser el conjunto una función, entonces:
* Si: x = 0 → F =5
2 2 (0)
(2; a - 3a) ∈ F ^ (2; 2a - 6) ∈ F → a - 3a = 2a - 6
2
2 Luego: F = a(0) + b → b = 5 ......... (2)
→ a - 5a + 6 = 0 (0)
Resolviendo: a = 2; a = 3 Reemplazando: (2) en (1) → a = 3
∴ a . b = 15
También: (4;a) ∈ F ^ (4; b - 1) ∈ F → a = b - 1
* Si: a = 2 → b = 3 ; reemplazando en F: 3. Dada la regla: F(x) = C (C ∈ Q-)
F = {(2; 5), (2; -2), (4; 2), (2; -2), (4; 2)} Tal que:
→ F = {(2; 5), (2; -2), (4; 2)} No es función. 2
F(7) + F(5) = 20
Hallar: F(2003) + F(2004)
* Si: a = 3 → b = 4 ; reemplazando en F:
F = {(3; 5), (2; 0), (4; 3), (2; 0), (4; 3)} Resolución: F(x) = C (función constante)
→ F = {(3; 5), (2; 0), (4; 3)} Si es función. 2
* Dado: ( F(7) ) + ( F(5) ) = 20
Luego, piden: F + F[F - 3] = F +F = C C
(4) (3) (4) (2)
2
Tenemos: C + C = 20
2. La tabla muestra los valores hallados para la Resolviendo: C = -5 v C = 4
función: Condición: C < 5 ∴ C = -5

29. Funciones Cuarto Año
Luego: F(x) = -5 ∴∀ x ∈ R * x = 1 → F(1) = 7
∴ F(2003) + F(2004) = -5 + (-5) = -10
1 + 3a = 7 → a = 2 Luego: b = 8
4. Indicar la suma de elementos del dominio de:
b c b
F = {(a;b), (1;7), ( 2 ;c), ( 2 ;11)} * x = 2 = 4 → F(4) = c
Si: F(x) = x + 3a 4 + 3a = c → c = 10
Resolución: de la función tenemos:
* x = a → F(a) = b Luego: F = {(2;8), (1;7), (4;10), (5;11)}
a + 3a = b → 4a = b
∴ Dom(F) = {2,1,4,5} → suma = 12
problemaS para la claSe
1. ¿Cuáles de las siguientes relaciones, Representa una función, calcular "ab".
representan funciones? a) 6 b) 9 c) 12
R = {(4;2), (5;8), (9;2), (3;7)} d) 15 e) 18
1
R = {(2;8), (3;9), (2;7), (9;5)}
2 5. Si: F = {(2; a+3), (2; 2a-1), (4; b+3), (a; 3b +
R = {(5;4), (6;8), (7;8), (2;8)} 1), (5; 2)}
3
R = {(9;6), (7;4), (7;8), (7;3)} Es función, calcular "ab".
4 a) 2 b) 4 c) 6
R = {(6;3), (6;3), (6;3), (9;8)} d) 8 e) 10
5
a) R , R b) R , R , R c) R , R
1 2 1 3 5 2 4 6. Dada la función:
d) R , R e) Todas F = {(5;8), (5;a-1), (3;2b), (10; 1), (3; b + 7)}
4 5
Calcular:
2. Señale cuál de las siguientes relaciones son
funciones: E = F(a - 6) + F(b + 3)
R = {(3;2), (5;2), (7;2)} a) 11 b) 12 c) 13
1
d) 14 e) 15
R = {(5;1), (4;3), (8;9), (5;3)}
2
R = {(5;3), (5;4), (5;5)} 7. Si el conjunto de pares ordenados:
3
2
R = {(5;3), (7;8), (6;5), (9;11)} F = {(2;a ), (2;16), (8;a+b), (8;6), (b;5)}
4
Representa una función, indicar la suma de
R = {(5;5), (6;6), (7;7), (8;8)}
5 elementos del dominio.
a) Todas b) R , R , R c) R , R a) 16 b) 18 c) 20
3 4 5 1 3
d) R , R , R e) R , R d) 22 e) 24
1 4 5 2 4
8. Si la relación:
3. Si el siguiente diagrama corresponde a una 2
función: F = {(3; a ), (a; a+1), (2; 5), (3; a+2)}
F Es una función, calcular el valor de:
E = F(F(a) + 2) - F(2 - a)
A B a) 1 b) 2 c) 3
1 2a d) 4 e) 5
1
2
7 9. Sea F una función definida por:
5 3 a -5 F = {(7;3a-1), (a;a-1), (3;a-2), (4;a+2),(5;2a)}
7 9 si: F(2 + F(n)) = a - 1
Halle el valor de "n".
Entonces, la suma de elementos del rango de a) 3 b) 4 c) 7
F, es: d) 5 e) 8
a) 27 b) 22 c) 16
d) 15 e) 10 10.Sea f(x) una función lineal tal que:
f(4) = 1; 2f(2) = 3f(3)
4. Si el conjunto de pares ordenados: entonces podemos afirmar:
F = {(1;2a+1), (a;b -1), (1;a+4), (3;5), (4;6)} a) f(2)=2 b) f(3)=1 c) f(10)=5

30. d) f(-2)=7 e) f(2)+f(8) = 3 x ∈ IR - {-d}, para la cual se realiza una
tabulación:
Bloque II x 1 4 -11 ...
1. Dada la siguiente función: F(x) 3 2 m ...
 ax + 5 ; x ≥ 4 Hallar "m".
f (x) =  a) -4 b) -3 c) 1/4
 3bx − 7; x < 4 d) 1 e) 2
Sabiendo que: f(6) - f(2) = 2(7 - 3b)
Calcular: f(f(12)) 7. Dada la función:
a) 4 b) 6 c) 8 F = {(a; b), (3; c), (1; 3), (2b; 4)}
d) 10 e) 12 Además: F(x) = x - 2a
Indique el producto de elementos de D ∩ R
2. Sea la función definida por: F F
f = {(3;9), (a-1; b), (3; 2a - 1), (b;2b + 3), a) 1 b) 2 c) -3
(9;b+1)} d) -1 e) 3
si: f(f (f (4) ) ) = b + 1, entonces el valor de
"b" es: 8. Sea la función:
a) 5 b) 6 c) 7 F = {(24;a+6), (a;a-1), (3;a-2), (4;a-2),(a;2a)}
d) 8 e) 3 Si se cumple: F(2 + F(n)) = a + 1
El valor de "n" es:
3. ¿Cuáles de las siguientes gráficas no son a) 3 b) 4 c) 7
funciones? d) 5 e) No se puede determinar.
y y y
9. Halle el área de la región sombreada en el
x x x
siguiente gráfico:
I. II. III. y
y y y
x x x
IV. V. VI.
a) II b) III y V c) I, III, VI
x
d) III y VI e) IV, V 1
4. ¿Cuál de las siguientes gráficas corresponde al
de una función? f(x ) = 9 - x
2
y y
2
x x a) 20µ b) 6 c) 24
I. II. III. d) 18 e) 32
y
x 10.Halle la longitud del segmento PQ en la
gráfica mostrada.
y
y y y
x x x P
IV. V. VI.
a) II,IV,V b) II,III,V c) I,III,V Q
d) I,III,IV e) Todas
x
5. La siguiente tabla: -1 4
x 2 4
y 2a + b + 5 2b
Muestra los valores hallados para la función: f(x ) = x 3- 9 x
F(x) = a |x - 5| + b
Calcular "b". a) 36 b) 28 e) 24
a) 4 b) 5 c) 6 d) 20 e) 21
d) 7 e) 8
c Bloque III
6. Dada la función definida por F(x) =
x+d

31. Funciones Cuarto Año
1. Se define la función: f(2) + f(5) = 42 ............ (2)
2x + 3 si: x < 3 a) 7 b) 4 c) 12
 d) 21 e) 6
f(x) = | x − 5 | si: 3 ≤ x < 7
 x + 3 si: x ≥ 7 6. Sea f(x) una función lineal que pasa por los

puntos (4;7) y (5; G(4)) donde G(x) = 2x + 2,
Calcular:
halle para que valor de x, f(x) y G(x) toman el
f(9) - f(f(3))
mismo valor.
a) 3 b) 4 c) 5
a) 3 b) 7 c) 8
d) 0 e) 7
d) 9 e) 6
2. Hallar "ab" de la gráfica:
y 2
f ( x ) = a x 3+ b 7. El área de la figura sombreada es de "a" µ .
Calcular "a".
y
(1 ;2 ) 2
(0 ;a ) f(x ) = 5 - x
2
x
-a a x
a) 1 b) 4 c) 6
d) 8 e) 10 a) 3 b) 5 c) 4
x d) 5/2 e) 3/2
3. Dada la gráfica de la función y = 2 + a, halle
la distancia del punto "P" al origen de
coordenadas. 8. Si F es una función constante que satisface la
y 3F(−2000 )
siguiente condición:
F(100 π) − 1
P
Entonces, el rango de F es:
4 a) -2 b) {-3} c) {-2}
d) {2} e) {3}
x 9. A partir de la función.
2 F = {(7;6), (7;a-2), (5;2b), (9;8), (5;b+3)}
Calcular:
E = F(a-3) + F(b+6)
a) 38 b) 32 c) 53 a) 24 b) 22 c) 14
28 45 d) 18 e) 15
d) e)
10.Sea f(x;y) con dominio x ∈ R; y ∈ R tal que:
4. Sean las funciones definidas por:
f = {(x;y) ∈ R x R / f(x) = 3x + 2}  − xy si: x ≥ 0 ∧ y ≥ 0
g = {(4;n), (7;n+1), (n+1;5)} 
 x
si: f(4) + g(g(a)) = 19  si: x < 0 ∨ y < 0
Halle el valor de "a". f(x; y) =  y
a) 4 b) 7 c) 11 si: x ∈ <0; 1> entonces:
d) 5 e) 9 2 4
E = f[ f [ (1-x) ; y ]; (x-1) ]
5. Halle la pendiente de una función f(x) lineal, se reduce a:
tal que: 2 2
a) y(1-x) b) -x c) -y
f(x+y) = f(x) + f(y) ....... (1) d) x - 1 e) xy
Tarea Domiciliara
1. Si se cumple:
(2x-1; 8) = (5; y+5); Calcular "x+y" 2. Si se cumple:

32. (5; a+1) + (b -1; 6) = (14;8); Hallar "b-a". F G
3. ¿Cuántos pares ordenados posee A x B, si: 5 2 b
A = {x ∈ IN / "x" es par ^ 2 ≤ x < 10 }
c 5 3 b -1
B = {x ∈ IN / "x" es impar ^ 6 < x ≤ 11 }
m a c
4. Sean los conjuntos:
A = {4;5;6} Si: G +G =G
(F(5)) [F(G(5))] [F(F(m))]
B = {1;2;3} Hallar "b".
y la relación R, definida por:
R = {(x;y) ∈ A x B / x + y ≤ 6} 13.Obtener el valor de n(A x B), si:
El número de elementos de R es: x −1
5. Dado el conjunto A = {1;2;3} A = {x ∈ IN /1 ≤ 5 < 2}
Se define la relación: B = {x ∈ IN / |x-5| = 8}
R = {(x;y) ∈ A x A / x + y ≥ 5}
Obtener el número de elementos de R. 14.Dados los conjuntos:
A = {3; 5; 7}
6. ¿Cuántas de las relaciones siguientes son B = {2; 4; 6}
funciones? Se definen las relaciones:
R = {(2;2), (3;2), (4;2)} R = {(x;y) ∈ A x B / x + y = 9}
1 1
R = {(1;0), (1;2), (3;3)} R = {(x;y) ∈ A x B / y = 4}
2 2
R = {(-1;0), (-1;1), (2;3)} Obtener: R ∩ R .
3 1 2
R = {(1;0), (1;1), (1;2)}
4 15.Sea: A = {1; 2; 3; 4; 5} y las relaciones
R = {(-1;1), (1;2), (2;1)} definidas por:
5
Justificar su respuesta. R = {(x;y) ∈ A x A / x = 2y}
1
2
7. ¿Cuál de las siguientes gráficas representa una R = {(x;y) ∈ A / x + y = 5}
2
función? ¿Cuántos elementos tiene R ∪ R ?
y y y 1 2
x x x 16.Indicar aquellos conjuntos que representan
a) b) c) funciones:
y R = {(1;2), (2;4), (3;5)}
y
1
x R = {(1;2), (3;6), (5;2), (5;4)}
x 2
d) e) R = {(3;5), (4;6), (2;1)}
3
R = {(4;6), (4;3), (4;3)}
4
8. Si el conjunto: R = {(3;2), (4;5), (3;1)}
5
F = {(7;a+1), (a;b-2), (7;6), (5;1), (1;3)}
Es una función, calcular "a-b".
17.Indicar cuántas gráficas corresponden a una
función:
9. Si el siguiente conjunto: y y y
F = {(1;2a), (2;2b-1), (5;1), (1;3a-5), (2;7)}
Es una función, calcular F(a-b). x x x
10.Hallar la suma de los elementos del rango de
2 y y y
la función: F = {(2;5), (3;a ), (3;4), (a;10)}
x x x
11.Hallar el valor de "y - x", si:
(3x + y; 2x - 5) = (23; x + 1)
18.Hallar el dominio de la función:
12.El diagrama muestra 2 funciones A y B: F = {(b; a-1), (9; b+3), (a+1; 2a-7), (2a-1; a),
(a+1; 3)}
19.A partir de la función:

33. Funciones Cuarto Año
F = {(2; a+2), (a; b-2), (2; 2a-1), (8; a+5),
(3; 14-b)} 25.Si se cumple:
Calcular: F(a) + F(b) (2x-3; 5) + (3x -7; y + 2) = (7y + 1; 9)
Calcular el resultado de: E = (2; 3) + (x; y)
20.Dada la función:
2 26.Hallar "a+b" a partir de la función:
F = {(4; 8), (b; 3), (5; a ), (4; a+b), (5; 9)}
a−3 b+3
Obtener: F(b) + F(5) + b
F = {(2; c + 2 ), (3;6), (2; 1 − c ), (9;4), (2;3)}
21.Hallar la suma de los pares ordenados (a;b)
que verifican la igualdad: 27.Dada la función:
2 F = {(1;8), (2;6), (3;-1), (4;7), (5;-11)}
(2a; a + b) = (b; 3) Construir el conjunto A, definido mediante:
22.Dados los conjuntos: A = {x / F(x+1) ≥ 1}
A = {x ∈ IN / x = y + 2 ∧ 1 < y ≤ 4}
B = {x ∈ IN / x = 2y ∧ 6 < y ≤ 10} 28.Se definen las siguientes funciones:
Calcular: n(A x B) F = {(x;y) ∈ R x R / y = 3x + 2}
G = {(4;n), (7;n + 1), (n+1;5)}
23.Con los conjuntos de la pregunta anterior, se Si: F +G = 19
construye una relación R, dada por: (4) [G(a)]
R = {(x;y) ∈ A x B / y = 3x + 2} Calcular "a".
Se pide calcular cuántos elementos conforman
la relación. 29.Dada la función:

  1 1  
G =  (1; y − 2), ( y;1 − z), (3;1)  ; , ( x; x )

24.Se define una función F, mediante:   
  x −3 5−x  

F = {(a;x+5), (b;x), (a;y+7), (c;d), (b;3y)}
Calcular el valor de "x.y". Donde: G ⊂ R x R ; x ∈ ZZ
Calcular "x + y + z"
Dominio y rango De una funcion
Dada una función real "F". y
F:R→R
Si: (x; y) ∈ F entonces: y = F(x) 3
Donde recordaremos que:
x = Pre - imagen F
y = Imagen de "x" mediante F. -2
x
5
Dominio y rango
1. Todos los pares ordenados (x; y) se pueden
graficar en el plano cartesiano, recordando que -1
el dominio (conjunto de pre-imágenes) está
relacionado con el eje de abscisas; y el rango Determinar el dominio y rango.
(conjunto de imágenes) está relacionado con Resolución: de acuerdo a las indicaciones
el eje de ordenadas. anteriores.
2. Cuando se tiene la gráfica de una función en el y
plano cartesiano, para hallar el:
a) Dominio: se proyecta la gráfica
perpendicularmente sobre el eje "x" (abscisas), 3
y se unen los intervalos resultantes. R
b) Rango: Se proyecta la gráfica A
perpendicularmente sobre el eje "y" -2
x N
(ordenadas), y se unen los intervalos 5
resultantes. G
• Ejemplo: Dada la gráfica de una función F. O
-1
D O M I N I O
DOM (F) = [-2;5>

34. RAN (F) = [-1; 3> 3x
4. Hallar el rango de: F(x) =
x+5
CRITERIOS PARA CALCULAR EL DOMINIO Y
RANGO
3x
Resolución: y = (Rango : valores de "y")
Dada una función real "F" con regla de x+5
correspondencia y = F(x), para obtener el: → y(x + 5) = 3x
a) Dominio, se despeja "y" en función de "x", yx + 5y = 3x
analizando los valores que pueden tomar "x" yx - 3x = -5y
de forma que "y" exista. − 5y
b) Rango, se despeja "x" en función de "y" x(y - 3) = -5y → x =
analizando los valores que puede tomar "y" de y −3
forma que "x" exista. − 5y
Las condiciones que deben cumplir las Luego; si ∈R→y-3≠0
y −3
variables analizadas (condiciones de
existencia) de manera que sean reales, son: y≠3
A PAR ∴ RAN(F) = IR - {3}
∈ IR → B ≠ 0 A ∈ IR → A ≥ 0
B 1. Hallar el dominio de la función "F" definida
por:
EJEMPLO DE APLICACIÓN 4 2
1. Hallar el dominio de: F(x) = x−4 F(x) = 16 − x
Resolución: De acuerdo a las condiciones de
Resolución: x − 4 ∈ IR → x - 4 ≥ 0 existencia:
x≥4 4
Graficando: 16 − x 2 ∈ IR → 16 - x2 ≥ 0
2
Multiplicando por (-1): x - 16 ≤ 0
Factorizando: (x+4)(x-4) ≤ 0
Punto críticos: x = -4 ∧ x = 4
-∞ 4 +∞
El intervalo solución de "x" será el dominio de
Graficando:
F. -
+ +
∴ DOM(F) = [4; +∞>
-∞ -4 4 +∞
4x ∴ DOM (F) = [-4;4]
2. Hallar el dominio de: G(x) =
x−7
4x 2. Proporcionar el dominio de:
Resolución: ∈ IR → x - 7 ≠ 0 4
x +1 − 4 − x
x−7
x ≠ 7 G(x) = 2x − 6
Es decir, G(x) no existe cuando x = 7 Resolución: El dominio de G(x) se obtendrá:
4
∴ DOM(G) = IR - {7} * x +1 ∈ IR → x + 1 ≥ 0
x ≥ -1 ................. (α)
2
3. Determine el rango de: H(x) = x + 4
Resolución: para el rango, despejamos "x" en 4 − x ∈ IR → 4 - x ≥ 0
*
función de "y".
x ≤ 4 ................. (β)
2 2
y=x +4→x =y-4
y−4 * 2x - 6 ≠ 0 (denominador ≠ 0)
x=± ∈ IR → y - 4 ≥ 0 x ≠ 3 ................. (γ)
y≥4
Graficando: Los cuales deben cumplirse simultáneamente.
Luego, de (α), (β) y (γ):
x ≥ -1 ∧ x ≤ 4 ∧ x ≠ 3
-∞ 4 +∞ -1 ≤ x ≤ 4 ∧ x≠3
∴ RAN (H) = [4; +∞> DOM (G) = [-1;4] - {3}
3. Hallar el rango de la función:

35. Funciones Cuarto Año
3x 2 + 4 Hallar el máximo valor de la función.
Resolución: Dando forma a la regla de
2
F(x) = x − 4 correspondencia.
3x 2 + 4 x +1 2
y = F(x) = =1+
2
Resolución: Sea y = F(x) → y = x − 4 x −1 x −1
2 2 * Usando dato: m ≤ x ≤ m + 2
* Despejando "x": y(x - 4) = 3x + 4 Restamos 1: m - 1 ≤ x - 1 ≤ m + 1
2 2 Como m < -1, entonces m + 1 < 0
yx - 4y = 3x + 4
2 2 1 1 1
yx - 3x = 4y + 4 ≤ ≤
2 Luego: m +1 x −1 m −1
x (y - 3) = 4(y+1)
Multiplicando por 2:
4( y + 1)
2 2 2
2 y −3 ≤ ≤
x = m +1 x −1 m −1
y +1
2 2 2
y −3 m +1 ≤ 1 + x −1 ≤ 1 + m −1
Entonces: x = ± 2 Sumando 1: 1 +
m+3 m +1
y +1
m +1 ≤ F(x) ≤ m −1
y −3 
  

* Luego, si x ∈ IR → ≥0 mínimo máximo
Resolviendo: puntos críticos -1; 3 valor de F valor de F
m +1
∴ máximo valor de F = m − 1
+ - +
6. Calcular el dominio de la función:
-∞ -1 3 +∞ 6 4 2
f(x) = x - 3x + 3x - 12
RAN (F) = <-∞ ;-1] ∪ <3; +∞> Sabiendo que el rango es:
RAN(f) = <-12 ; 16>
2
4. Dada la función F(x) = x - 1 con dominio en
el intervalo Resolución:
[-4;-2] ∪ [-1;1] Se sabe que: f(x) ∈ <-12,16>
Hallar el rango. → -12 < f(x) < 16
Resolución: 6 4 2
-12 < x - 3x + 3x - 12 < 16
En este caso, vamos a obtener el rango a
partir del dominio. Sumando (11) a cada miembro.
Del dato, podemos afirmar que: 6 4 2
-4 ≤ x ≤ -2 v -1 ≤ x ≤ 1 -12 + 11 < x - 3x + 3x - 12 + 11 < 16 + 11
Elevando al cuadrado las inecuaciones: 6 4 2
- 1 < x - 3x + 3x - 1 < 27
2 2 2 3
4 ≤ x ≤ 16 v 0≤x ≤1 -1 < (x - 1) < 27
Restando 1 a cada miembro:
2 2 2
3 ≤ x - 1 ≤ 15 v -1 ≤ x - 1 ≤ 0 Extrayendo raíz cúbica: -1 < x - 1 < 3

  
  2
Sumando 1: 0<x <4
F( x ) F(x)
2 2
→ 0 < x ∧ x < 4 ; resolviendo:
Luego: RAN(F) = [-1; 0] ∪ [3; 15] → x ∈ IR ∧ x ∈ <-2 ; 2>
→ x ∈ <-2 ; 2>
5. Siendo m < -1; se define la función F por ∴ DOM(f) = <-2 ; 2>
x +1
medio de F(x)= ; x ∈ [m;m+2].
x −1
problemaS para la claSe

36. Bloque I 4
9−x
1. Hallar el dominio de las siguientes funciones: x +1 +
3 2
* F(x) = 4x + 8x + 7 F(x) = x −5
2
4 x + 5x
6. Hallar el dominio de:
* G(x) = 3
5
4x − 3 2 F( x ) = x − 4 + 10 − x +
+ x −6
* H(x) = x − 5 x+3 a) [4; 10] - {6} b) [4; 6]
3 5 3 c) [4; 6] ∪ {0} d) [4; +∞>
+ + e) [6; 10]
* I(x) = 4 x−4 x
7. Dada la función definida por:
2. Hallar el dominio en:
F(x) = |x - 5| + x + 2
* F(x) = x − 5 + 3x2
Si DOM(F) = {2; 7; 14}, indicar la suma de
4
7−x +
3 elementos del rango.
* G(x) = x − 4 - x
a) 24 b) 23 c) 22
4 x d) 21 e) 20
x −2 +
* H(x) = x −5
8. Hallar el rango de la función:
3. Relacionar las funciones con sus respectivos 4x − 1
dominios:
F(x) = x + 2
4
F(x) = 3x - 7x + 2 I. x ∈ IR - {9 ; 10} a) IR - {-4} b) IR - {4} c) IR - {2}
II. x ∈ IR - {0 ; 3} d) IR - {-2} e) φ
1 3x
+ 9. Dada la gráfica de la función F(x):
G(x) = x − 3 x −7 III.x ∈ IR - {0} y
IV. x ∈ IR - {0 ; 9}
8
2 x 4
+ − 4
H(x) = 3 x − 9 x V. x ∈ IR
-5 -2
VI. x ∈ IR - {3 ; 7} x
3 9
a) F-I; G-II; H-V b) F-II, G-V; H-VI
c) F-V; G-VI, H-IV d) F-V; G-VI; H-II
e) F-V; G-VI; H-I -7
4. Relacionar las funciones con sus respectivos Obtener el dominio y rango.
dominios:
10.A partir de la gráfica de la función F(x):
F(x) = 2x + x −6 I. x∈[1;+∞>-{3} y
II. x∈<-∞,6]
4 6 5 3
G(x) = x − 2 + 10 − x − x III.
4
x∈[2;10]
IV. x∈[2;+∞> 8
3x 2 x
-6 -2 4 7
+ x −1
H(x) = x − 3 V. x∈[6;+∞>
VI. x∈[1;+∞> -3
a) F - II; G - I, H – IV b) F - V; G - II; H - III
c) F - IV; G - I; H - V d) F - V; G - III; H - I
e) F - VI; G - III; H - I Calcular el DOM(F) ∩ RAN(F), e indicar la
suma de elementos enteros del conjunto
5. Hallar el dominio de la función: pedido.
a) -4 b) -3 c) -2
d) -1 e) 0

37. Funciones Cuarto Año
Calcular: DOM(F) ∩ RAN(G)
Bloque II a) <-1; 2> b) <-1; 2] c) [-1; 2>
1. Hallar el rango de la función: d) [-1; 2] e) [-1; +∞>
6x + 1
2
10.Dada la función: F(x) = 2x + 3x + 2; x ∈ IR
F(x) = 2 x − 3
a) R - {3/2} b) R - {-3} c) R - {-3/2}  a
d) R - {3} e) φ a +1 ;+ ∞ >
Donde RAN(F) = 
2. Hallar el rango de: Calcular el valor de "a".
2 a) 6 b) 7 c) 8
F(x) = x + 4x + 7; x ∈ IR d) 9 e) 10
a) IR b) [1; +∞> c) [3; +∞>
d) <-∞; 1] e) <-∞; 3] Bloque III
1. Dada la función definida por:
3. Hallar el rango de:
F(x) = |x - 3| + x + x + 1
2
2
F(x) = x - 6x + 5; x ∈ IR
Si: DOM(F) = {3,8,0}, indicar la suma de
a) <-∞; -4] b) [-4; +∞> c) <-∞; 4]
elementos del rango.
d) <-∞; 0] e) [4; +∞>
a) 86 b) 81 c) 87
d) 85 e) 83
4. Si el rango de la función:
F(x) = |x - 4| - 2
2. Dada la gráfica de F(x):
es RAN(F) = [-2; 3] y
Hallar el dominio.
5
a) <-1; 8> b) [-1; 9] c) [-9; -1]
d) [-1; 8] e) <-1; 9>
-7 -2
x
2 1 7
5. Dada la función F(x) = |x - 12| + 5 -1
con DOM(F) = <2; 4>
Calcular el RAN(F) -5
a) <5; 13] b) [5; 13> c) <5; 13>
d) [5; 13] e) <5; +∞> Se cumple: DOM(F) ∩ RAN(F) = [a;b> ∪ [c;d]
Calcular "a + b + c + d"
2 a) 0 b) 1 c) -3
6. Dada la función: F(x) = |x - 9| + 2 con d) 13 e) -13
dominio = [2;7]
Obtener el rango de la función. 3. ¿Cuántos enteros presenta el dominio de la
a) <2; 40] b) [2; 42> c) [2; 42> función?
d) [2; 42] e) [2; 40]
4 −x+2 3x
+
7. Calcular el dominio de la función: F(x) = x − 10 x −7
F(x) = |2x - 7| - 8 a) 6 b) 7 c) 8
Sabiendo que el rango es: RAN(F) = <-5; 1] d) 9 e) 10
a) [-1; 2> ∪ <5; 8] b) <+2; 13]
c) <1, 13> d) [1; 5] 4. ¿Cuántos enteros presenta el dominio de la
e) [0; +∞> función?
4 1
8. Obtener el número de elementos enteros del − x 2 + 7x − 6 +
dominio de la función: F(x) = x−4
x−3 + 3−x
F(x) = x2 − 1 5. Obtener la suma de elementos enteros del
a) 7 b) 6 c) 5 rango de la función:
d) 4 e) 3 F(x) = ||x+1| - 2|
Si se conoce que DOM(F) = [-3;1>
9. Dadas las funciones "F" y "G" de variable real: a) 0 b) 1 c) 2
d) 3 e) 4
2−x
6. Hallar el dominio de la función:
F(x) = x − 2 ; G(x) = x + 6x + 8; ∴∀ x ∈ IR
2
2
F(x) = x - x + 1

38. 3  1
 4 ; 1
Si su rango es   9. Sea la función: F(x) = x − 5 + 8 − x
a) <0; 2> b) [0; 1] c) <-2; 2> (x ∈ ZZ )
d) <-3; 3> e) <0; 4> Si la suma de los elementos del rango es:
2 3+ 2
7. Sea la función F(x) = -2(x - 4) + 8 cuyo +a+ a
dominio pertenece al intervalo [a; 4] 6
Hallar "a + b", sabiendo que el rango está
Indicar el valor de "a".
dado por [6; b]
a) 1 b) 2 c) 3
a) 5 b) 6 c) 7
d) 4 e) 5
d) 9 e) 11
10.Hallar el dominio de la función:
8. Calcular el dominio de la función:
2n
| x + 7| −| x − 3| | x − 3 | +x − − x
F(x) = (n ∈ IN) F(x) =
a) <-∞; -2] b) <-∞; 2] c) φ a) <-9; 0> b) [-9; 0> c) [-9; 0>
d) [-2; +∞> e) IR d) [-9; 0] e) <-∞; 0]
Tarea Domiciliaria
1. Hallar el dominio de la función F, cuya gráfica
es: 9. Obtener el rango de la función:
y
2
7 H(x) = x - 2x + 3; x ∈ IR
-9
x
10.Si el rango de la función: F(x) = x + 2
5 Es <5;7], entonces el dominio de F es:
-4
11.Obtener el rango de la función F, cuya gráfica
es:
y
2. Calcular el dominio de la siguiente función: 8
6x − 1 5
F(x) = x − 7
-6
x
-4 3 6
3 x+8 -2
3. Obtener el dominio de: F(x) = 7x +
4. ¿Cuántos enteros presenta el dominio de la -1 0
4 8
F(x) = 1−x + x+8
función: ? a) <-6; 8> b) <-6; 3] c) [-10; 8]
d) [-6; 3> e) [-6; 6>
5. Determinar el dominio de:
12.Relacionar cada función con su dominio:
H(x) = 30 − x − x 2
4x
2 I. F(x) = x − 6 a. IR - {-10}
6. Sea: M(x) = x - 5 5 6x
Con dominio = {2; 3; 4} +
Entonces, los elementos del rango suman: II. G(x) = x x−8 b. IR - {6}
7. Hallar el rango de h(x) = 5 - 2x x +5 6
Si se sabe que DOM(h) = <-3;4] +
III. H(x) = 3 x + 10 c. IR - {0; 8}
8. Hallar el rango de:
13.Determinar el dominio de:
3x − 1
F(x) = 2 x − 5

39. Funciones Cuarto Año
3 y
3−x 4 10
+ 2x − 1
F(x) = x −2
1
14.Hallar el dominio de: -1
x
-2 1
4
F(x) = 2 x + 1 + 3x − 1 -1
-2
15.En la función:
x +1 4x Calcular: DOM(F) ∩ RAN(F)
+
G(x) = 2−x x −1
22.Hallar el dominio de:
El dominio es de la forma [a;b> - {c}
Calcular "a", "b" y "c" (en ese orden) 3x 2 − 2
3 2
G(x) = x + x − 20 x
16.Señale la suma de elementos del conjunto de
2 23.Obtener el dominio de la función:
imágenes de la función: F(x) = x + 2
6
siendo DOM(F) = {-2; -1; 1; 2} | x − 14 | − | x + 4 |
G(x) =
2 24.Dada la función:
17. Sea la función F(x) = x + 4x + 9, cuyo
dominio es: 4−| x| 3x
x ∈ <-10; 3]. Si el rango es: y ∈ [a;b> 4 + 2
| x − 3| x −1
b−a G(x) =
Calcular: Indicar el número de elementos enteros de su
dominio.
18.Hallar el rango de:
6x − 1 25.Hallar el rango de la siguiente función:
F(x) = |x-3| + x
F(x) = 2 x − 10
26.Calcular "m", sabiendo que el rango de la
2 función:
19.Se define la función F(x) = -x + 10x - 21, x ∈ IR.
Entonces el máximo valor que puede admitir F es: 5m + 1
2
F(x) = -3x + x + 5 es de la forma <-∞; m ]
20.Dada la función H(x) = |x - 1| - 5, la cual tiene
27.Determine el rango de la función:
RAN(H) = [-5 ;1>. Calcular la cantidad de
elementos enteros no positivos que posee el H(x) = (|x - 5| + 1 + x). 5−x
dominio. x+6
21.Dada la gráfica de la función "F". 28.Dada la función H(x) = x + 1
Si: DOM(H) = <2;3], hallar el rango.
29.Hallar el dominio de la función:
3 2
F(x) = x + 3x + 3x - 3
Si su rango es RAN(F) = <-5;60]
Dar como respuesta el número de valores
enteros que posee.
grafica De una función
Sabemos que los pares ordenados (x;y) que conforman la función y = F(x) se pueden ubicar en un plano
cartesiano. Esta representación geométrica se le conoce como GRÁFICA DE UNA FUNCIÓN.
Ejemplo:
* Graficar la función: F(x) = 2x - 1 , sabiendo que: DOM(F) = {-2; -1; 0; 1; 2}
Resolución:
Obteniendo los pares ordenados de F.
x = -2 → F(-2) = -5 → (-2; -5) ∈ F

40. x = -1 → F(-1) = -3 → (-1; -3) ∈ F
x = 0 → F(0) = -1 → (0; -1) ∈ F
x = 1 → F(1) = 1 → (1; 1) ∈ F
x = 2→ F(2) = 3 → (2; 3) ∈ F
y
4
G r á f ic a d e F ( x )
3
2
1
1 2 3
-3 -2 -1 0 x
-1
-2
-3
-4
-5
* Luego, ubicamos los pares ordenados:
FUNCIONES NOTABLES
FUNCIÓN CARACTERÍSTICA GRÁFICA
(C > 0 )
y
C
C : Constante
Constante
DOM(F) = R
F(x) = C
RAN(F) = {C}
x
y
C
IDENTIDAD RAN(F) = R
F(x) = x DOM(F) = R
45º
x

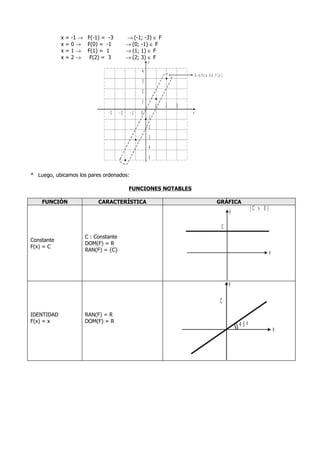
41. Funciones Cuarto Año
y
y
b
a: Pendiente
LINEAL b
b : Intersectado con "y"
F(x) = ax + b
RAN(F) = R
(a ≠ 0) x
DOM(F) = R
x
a>0
a<0
V: vértice de la parábola (h; k) a>0
b y RAN(F) = [k;+∞>
h=-
2a k V (h ;k )
CUADRÁTICA y
2
∆
F(x)= ax + bx + c k=- ó
4a
(a ≠ 0)
Donde:  b  h x h
k = f − 
2  2a 
∆ = b - 4ac x
DOM(F) = R a<0
k V (h ;k )
RAN(F) = De acuerdo a la RAN(F) = <-∞ ; k]
gráfica
y
3 RAN(F) = IR
F(x) = x
Cúbica DOM(F) = IR
x
y
 x; x ≥ 0
| x |= 
VALOR ABSOLUTO − x ; x < 0
F(x) = |x| +
45° 45°
RAN(F) = R
0 x
DOM(F) = R
y
+
RAN(F) = R
F(x) = x 0
RAÍZ CUADRADA +
DOM(F) = R
0 x

42. y
MULTIPLICATIVO
INVERSO DOM(F) = R - {0}
1 RAN(F) = R - {0}
F(x) =
x
x
TRAZADO DE GRÁFICAS ESPECIALES
Lo que viene a continuación es un conjunto de técnicas para trazar las gráficas de funciones más
complicadas, a partir de funciones básicas (estudiadas anteriormente)
F (x+ h ) F (x) F (x-h )
y
y y
HORIZONTAL
x x
h x h
DESPLAZAMIENTO
F(x) se desplaza a la izquierda Posición inicial F(x) se desplaza a la derecha
F (x) + h F (x) F (x) - h
y y y
VERTICAL
h
x
x x h
F(x) se desplaza hacia arriba Posición inicial F(x) se desplaza hacia abajo

43. Funciones Cuarto Año
F (x) F (-x)
y y
HORIZONTAL
x x
Posición inicial F(x) se refleja respecto al eje "y"
F (x) -F (x)
y y
VERTICAL
RFLEJOS
x x
Posición inicial F(x) se refleja respecto al eje "x".
F (x) |F (x)|
y y
VALOR ABSUTO
x x
R e fle jo d e
P a rte P a r t e N e g a t iv a
N e g a t iv a
La parte negativa de
Posición Inicial
F(x) se grafica sobre el eje "x".
Ejemplos: b = -4a ........... (β)
1. Obtener la pendiente de una función lineal "F", Reemplazando (β) en (α): a + (-4a) = 3
sabiendo que F(1) = 3 y F(2) = 2F(3) -3a = 3
Resolución: ∴ a = -1
* Si "F" es función lineal, entonces
F(x) = ax + b (donde a: pendiente) 2. Sea F(x) una función cuadrática cuya gráfica
pasa por los puntos (0;12), (2;0) y (3; 0).
* Datos: Hallar el valor de F(-1).
F(1) = 3 → a(1) + b = 3 → a + b = 3 ..... (α) Resolución:
F(2) = 2F(3) → a(2) + b = 2 [a(3) + b] * Si F(x) es cuadrática, luego

44. 2
F(x) = ax + bx + c. Para calcular F(-1) es
2
preciso obtener "a", "b" y "c". * Finalmente, la función F(x) = 2x - 10x + 12
∴ F(-1) = 24
* De los datos:
(0; 12) ∈ F → F(0) = 12 3. Graficar las funciones siguientes:
2 a) F(x) = |x-2|
a(0) + b(0) + c = 12 → c = 12
b) G(x) = |x| + 5
(2;0) ∈ F → F(2) = 0
2
a(2) + b(2) + 12 = 0 →2a + b = -6 .......... (α) c) H(x) = −x
(3;0) ∈ F → F(3) = 0 2
d) I(x) = (x+2) + 3
2
a(3) + b(3) + 12 = 0 →3a + b = -4 ........... (β)
Resolución:
a) F(x) = |x-2| b) G(x) = |x| + 5
F (x) F (x)
y y
y = |x | + 5
y = |x | y = |x -2 |
5
x y = |x |
0 x
La gráfica de F(x) se desplaza hacia la derecha La gráfica de G(x) se desplaza hacia arriba
2 unidades 5 unidades.
−x 2
c) H(x) = d) I(x) = (x + 2) + 3
y
y
y = √-x
y = √x
2
y = (x + 2 ) + 3 3
5 y = x 2
0 x -2 0 x
La gráfica de H(x) se refleja hacia la izquierda, En este caso ocurre doble
desplazamiento: (respecto al eje "y") 1. 2 unidades a la izquierda.
2. 3 unidades hacia arriba.
2
4. Graficar: F(x) = |x - 10|
Resolución: Usamos valor absoluto (ver cuadro anterior)

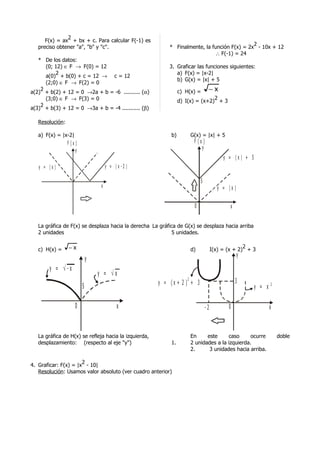
45. Funciones Cuarto Año
y
y 10
0 x
x
P a rte R e f le jo d e la
N e g a t iv a -1 0 P a r t e N e g a t iv a
2 2
F(x) = x - 10 F(x) = |x - 10|
y
5. Indicar la gráfica de F(x) = 7 - |x - 2|
Resolución: 7
* Gráfica 1: y = |x| (función valor absoluto)
y 1
f(x )
-2 x
Indicar el gráfico de f(-x) - 1
x
Resolución:
* y = f(-x) es simétrica a f(x) respecto al eje
* Gráfica 2: y = |x - 2| se desplaza dos "y". (reflejo horizontal)
unidades a la derecha. y
y
1
2 x
2 x
* Gráfica 3: y = |x - 2| es simétrica a:
y = - |x-2| con respecto al eje x. * y = f(-x) - 1 se desplaza una unidad hacia
(Reflejo vertical). abajo.
y y
2
x 2
x
-1
7. Sea la función F(x) descrita por el gráfico.
* Gráfica 4: y = 7 - |x - 2| se desplaza hacia y
arriba 7 unidades.
y
7
x
2 x
Indicar el gráfico de F(2-x)
Resolución:
6. Según el gráfico de f(x): * Nos piden graficar: y = F(2 - x) = F[-(x - 2)]
* Inicialmente: y = F(x)

46. y y
2
-1 x
x *
y
* Gráfica 1: y = F(x-2). Se desplaza 2 2
unidades a la derecha.
y 2
-1 x
b
2 x
Luego, el triángulo sombreado es la figura
* Gráfica 2: y = F[-(x - 2)]. Es simétrica en el
formada por la intersección de F(x) y el eje
eje "y" respecto a la función: y = F(x-2)
y "x", cuya altura conocemos
(2 unidades). Para hallar la base (b)
efectuamos:
2 - |x + 1| = 0
(Intersección con "x")
|x + 1| = 2
x + 1 = 2 v x + 1 = -2
x
x=1 v x = -3
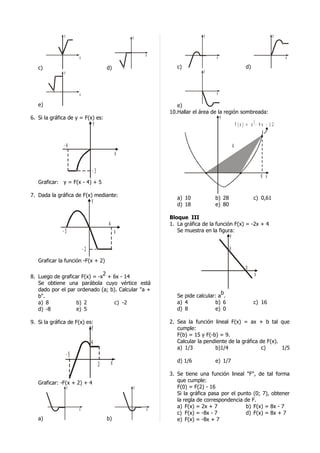
8. Hallar el área del triángulo formado por la
intersección de la función: F(x) = 2 - |x + 1| y Luego, la base "b" está dada por la separación
el eje "x". entre x = 1 y x = -3; es decir: b = 4
*
b×h 4×2
y
∴ área = 2 = 2 = 4µ2.
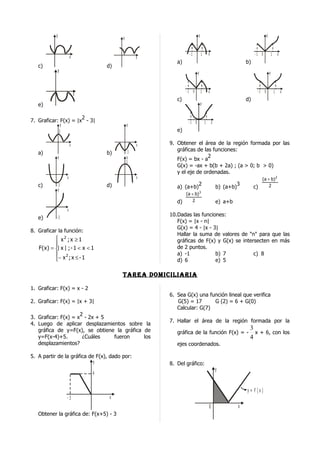
9. Sean las funciones
y = |x |
2
F(x) = x - 4x + 5 y G(x) = x - 1
Que presentan puntos "A" y "B" comunes entre
x
si. Si de dichos puntos se bajan
* perpendicularmente al eje de abscisas, indicar
y el área encerrada bajo la recta, el eje "x" y
dichas perpendiculares.
Resolución:
y = |x+ 1 |
* Graficando F(x) y G(x) en el plano:
y F
-1 x B
*
y A
1
-1
x
0 T 2 R x
-1
* "A" y "B" son puntos de intersección; al
bajar perpendiculares al eje "x" se obtienen

47. Funciones Cuarto Año
los puntos "T" y "R". La figura cuya área 2
x - 4x + 5 = x - 1 (Intersección)
nos piden calcular es el trapecio ABRT
Resolviendo: x = 2 v x = 3
Si: AT : base menor
x = 2→ G(2) = 1 → punto A = (2; 1)
BR : base mayor
x = 3→G(3) = 2 → punto B = (3; 2)
TR : Altura
Luego :
* Del gráfico, se puede calcular:
 AT + BR  AT = 1
Área =   TR ................ (α)
 2  1 + 2  3

 2  
BR = 2 Área =   1 = 2 µ2
Para calcular las bases, hay que obtener los
puntos "A" y "B":
TR=1
problemaS para la claSe
Bloque I y
1. Graficar las funciones siguientes:
a) F(x) = 2x – 4 b) F(x) = -3x + 12 2
x
2. Graficar las funciones:
a) F(x) = |x-2| + 4 b) F(x) = -|x-1| + 5 e)
3. Graficar las funciones: 5. La gráfica de y = F(x) es:
2 2 y
a) F(x) = (x-3) + 5 b)F(x) = 10x - x - 23
3
4. Graficar: F(x) = -|x - 6| + 2
y y
1
2 2 x
0 1 2 4
6 x 6 x ¿Cuál de las gráficas corresponde a la función
a) b) y = F(x+4) -3?
y y y y
2
x
6 x
x x
c) d) a) b)

48. y y y y
x
x x x
c) d) c) d)
y y
x x
e) e)
10.Hallar el área de la región sombreada:
6. Si la gráfica de y = F(x) es: y
y 2
F (x) = x - 4 x - 1 2
-4 A
x
-3
8 x
Graficar: y = F(x - 4) + 5
7. Dada la gráfica de F(x) mediante:
a) 10 b) 28 c) 0,61
y
d) 18 e) 80
Bloque III
4 1. La gráfica de la función F(x) = -2x + 4
-3 x Se muestra en la figura:
y
-2 a
Graficar la función -F(x + 2)
b
2 x
8. Luego de graficar F(x) = -x + 6x - 14
Se obtiene una parábola cuyo vértice está
dado por el par ordenado (a; b). Calcular "a +
b
b". Se pide calcular: a .
a) 8 b) 2 c) -2 a) 4 b) 6 c) 16
d) -8 e) 5 d) 8 e) 0
9. Si la gráfica de F(x) es: 2. Sea la función lineal F(x) = ax + b tal que
y cumple:
F(b) = 15 y F(-b) = 9.
4 Calcular la pendiente de la gráfica de F(x).
a) 1/3 b)1/4 c) 1/5
-5
x d) 1/6 e) 1/7
2
3. Se tiene una función lineal "F", de tal forma
Graficar: -F(x + 2) + 4 que cumple:
y y F(0) = F(2) - 16
Si la gráfica pasa por el punto (0; 7), obtener
la regla de correspondencia de F.
a) F(x) = 2x + 7 b) F(x) = 8x - 7
x x
c) F(x) = -8x - 7 d) F(x) = 8x + 7
a) b) e) F(x) = -8x + 7

49. Funciones Cuarto Año
4. Obtener el área de la figura formada por la Bloque III
10 − 2x 1. ¿En cuántos puntos se intersectan las gráficas de
F(x) = f(x) = 5 - x y g(x) = |x + 3|?
gráfica de la función 5 y los ¿Cuáles son estos puntos?
ejes cartesianos a) 1; (1,4) b) 2; (1,4) y (3,5)
2 c) 1; (3,5) d) 2; (1,5), (3,4)
a) 5 u b) 10 c) 15
d) 40 e) 20 e) 1; (1,5)
5. Hallar el área de la región formada por la 2. Si h es una función lineal de pendiente 3 e
función: intercepto con el eje "y" 5. Halle la regla de
2 correspondencia de la función g(x), si:
F(x) = - x + 4, con los ejes coordenados. g(x) - x = h(1) + h(x+1)
3 a) 4x + 4 b) 4x + 12 c) 4x + 16
2 d) 3x + 12 e) 3x + 16
a) 48 µ b) 16 c) 24
d) 12 e) 9/4
3. Sea la función lineal F(x) tal que pase por el
6. Determine el área de la región formada por la punto (4; 11).
gráfica de la función F(x) = - |x| + 4 y el eje Además: 2F(1) = F(2) + 3.
de abscisas. Calcular el valor de la pendiente.
2 a) 1 b) 2 c) 3/2
a) 8 µ b) 12 c) 16 d) 4 e) 3
d) 32 e) 64
4. Hallar el área de la región formada por las
7. Se tienen las funciones: gráficas de las funciones: F(x) = |x - 5| y
2 G(x) = 3
F(x) = x - 4x + 5 y G(x) = x - 1
Cuyas gráficas se cortan en los puntos "A" y 2
a) 18 µ b) 16 c) 12
"B". d) 9 e) 6
Se pide obtener la suma de las ordenadas de
dichos puntos. 5. Sean las funciones:
a) 5 b) 4 c) 3 2
d) 2 e) 1 f(x) = x - 2x - 3
g(x) = x + p
8. Las gráficas de las funciones: Cuyas gráficas se cortan en 2 puntos, tales
2 que al unirse forman la diagonal de un
F(x) = x + 8 y G(x) = 6x se intersectan en los cuadrado. Si uno de los puntos mencionados
puntos (a;b) y (c;d) es (3;0); hallar el área de dicho cuadrado.
Calcular: E = a + b + c + d 2
2 a) 3µ b) 6 c) 9
a) 36 µ b) 38 c) 40 d) 12 e) 15
d) 42 e) 44
6. Si la gráfica de la función y = F(x) es:
9. Indicar el área de la región formada por: y
F(x) = |x - 2| - 6 y el eje "x". 4
2
a) 36µ b) 18 c) 42
d) 15/2 e) 4/3
10.Halle el área de la región sombreada. -3 3 x
y
Graficar la función y = |F(x-2) - 3|
y y
-5
x x x
2 a) b)
F (x )= x -4 9
2
a) 72µ b) 144 c) 288
d) 36 e) 18

50. y y
y y
-1 1 x -1 0 1 x
x x
a) b)
c) d)
y y y
-1 0 1 x -1 0 1 x
x
c) d)
e) y
2
7. Graficar: F(x) = |x - 3| -1 0 1 x
y y
3 e)
x x 9. Obtener el área de la región formada por las
-3 gráficas de las funciones:
a) b)
y y 2
F(x) = bx - a
3
G(x) = -ax + b(b + 2a) ; (a > 0; b > 0)
y el eje de ordenadas.
x x ( a + b) 2
c) -3 d) 2 3 2
y
a) (a+b) b) (a+b) c)
3
(a + b)
d) 2 e) a+b
x
10.Dadas las funciones:
e) -3
F(x) = |x - n|
G(x) = 4 - |x - 3|
8. Graficar la función:
Hallar la suma de valores de "n" para que las
 x2 ; x ≥ 1 gráficas de F(x) y G(x) se intersecten en más

F( x ) = | x | ; - 1 < x < 1 de 2 puntos.
 2 a) -1 b) 7 c) 8
− x ; x ≤ - 1 d) 6 e) 5
Tarea Domiciliaria
1. Graficar: F(x) = x - 2
6. Sea G(x) una función lineal que verifica
2. Graficar: F(x) = |x + 3| G(5) = 17 G (2) = 6 + G(0)
Calcular: G(7)
2
3. Graficar: F(x) = x - 2x + 5
7. Hallar el área de la región formada por la
4. Luego de aplicar desplazamientos sobre la
gráfica de y=F(x), se obtiene la gráfica de 3
gráfica de la función F(x) = - x + 6, con los
y=F(x-4)+5. ¿Cuáles fueron los 4
desplazamientos? ejes coordenados.
5. A partir de la gráfica de F(x), dado por:
y 8. Del gráfico:
y
4
y = F (x)
-3 x
0 x
Obtener la gráfica de: F(x+5) - 3

51. Funciones Cuarto Año
Hallar el área de la región sombreada, y y
sabiendo que F(x) = |x-6|
9. Determinar los puntos de intersección de las x x
gráficas de las funciones: a) b)
y y
2
F(x) = x y G(x) = 3x - 2
10.Hallar el área de la región sombreada: x x
y c) d)
y
2
F (x )= -x + 9
x
e)
x
15.A continuación se muestra la gráfica de F(x):
y
11.La figura:
y
b x
-5 x
¿Cuál de las siguientes gráficas representa a la
función: -F(-x)?
y y
corresponde a la gráfica de F(x) = ax + 15.
Calcular "a+b".
x x
12.Si la gráfica de F(x) = |x - a| + b (a > 0; b >
a) b)
0)
Está dada por: y
y
x
c) d)
y
4 b -9
2 a -5 x x
e)
Calcular "a - b" 16.Sabiendo que la gráfica de una función lineal
pasa por los puntos (8;38) y (0;-2), se pide
13.Obtener el vértice de la parábola, cuya gráfica calcular la pendiente de dicha función.
2
está representada por F(x) = -x + 6x - 10. 17.Se tiene una función "F" cuya regla de
correspondencia verifica la igualdad:
14.Dada la gráfica de F(x): 2(3 - F(x) ) = x
y
Calcular el área de la figura que forma la
2 gráfica de "F" con los ejes coordenados.
18.Luego de graficar: F(x) = |x| - m (m > 0) se
-3 observa que dicha gráfica forma con los ejes
1 x 2
coordenados, un triángulo cuya área es 64µ .
-1 Calcular el valor de F(-2).
¿Cuál de las siguientes gráficas corresponde a 19.Halle los puntos de intersección de las gráficas
F(x-3) + 1? de:
2
F(x) = x - 4x + 17

52. G(x) = 3x + 5
E indique la suma de coordenadas de uno de 25.Sabiendo que F es una función lineal de
ellos. pendiente 3 e intersecta al eje "y" en 5;
obtener la regla de correspondencia de la
función G(x),
20. Dado el gráfico: si: G(x+12) - x = F(1) +
y
2
V 26.La gráfica de la función F(x) = x + bx + c es
una parábola que pasa por los puntos (0;2) y
(1;5). Luego, dicha gráfica está dada por:
x 27.La figura formada por las gráficas de F(x) = |
x-5| y G(x) = P (0 < P < 5) es un triángulo
2
cuya área es 16µ . Se pide graficar G(x).
2 y y
Donde: F(x) = -x + 6x - 5
Hallar el área de la región sombreada.
(V : Vértice de la parábola) x x
a) b)
2 y y
21.Graficar: F(x) = -|x - 1|
22.Si la gráfica de una función F(x) está dada por: x x
y
c) d)
y
x
x e)
28.Al graficar las funciones: f(x) = |x-5| y
G(x) = |x+3| ; se observa que hay solo un punto
de intersección entre ellos. Calcular la distancia
La gráfica de -F(-x) es:
de dicho punto hacia el eje de abscisas.
23.Graficar:
2
x2 ; x < 1 29.Graficar: f(x) = x - 2|x| - 3

F(x) = 
 5 ;x ≥ 1
 30.Hallar la relación que deben cumplir m y n
para que las gráficas de:
24.Si: (a - 2; b + 1) es el único punto de 2
F(x) = x + x + m
intersección de las gráficas de: F(x) = |x| y G(x) = n - 3x
G(x) = 6 - x Se intersecten en un solo punto.
Calcular "ab".

53. Logaritmos Cuarto Año
Tema nº 03: l o g a r i T m o S
Capacidades:
 Define logaritmo.
 Aplica propiedades de logaritmos.
 Resuelve ecuaciones con logaritmos
 Resuelve problemas con logaritmos, aplicando su definición y propiedades.
Desarrollo del Tema:
NOTACIÓN:
Log a → N ú m e r o d e l o g a r it m o ( a > 0 )
b
B a s e d e l lo g a r it m o ( b > 0 ∧ b ≠ 1 )
Se lee: Logaritmo de "a" en base "b".
DEFINICIÓN: El logaritmo se define como el valor (c) al que hay que elevar la base (b) para obtener el
número (a).
c
Asi: Log a = c ⇔ a = b
b
Donde: a>0
b>0;b≠1
Ejemplos. Calcular cada caso e indicar el número de soluciones
4
* Log 81 = 4 ⇔ 81 = 3 * Log 169 = ⇔
3 13
6
* Log 64 = 6 ⇔ 64 = 2 *Log 625 = ⇔
2 5
• Resolver: Log (3x - 2) = 2
x
Resolución:
De la definición:
2
Log (3x - 2) = 2 ⇔ 3x - 2 = x
2
x 0 = x - 3x + 2
x -2
x -1
Ahora tenemos que:
x=2 v x=1 (Posibles soluciones)
Pero: base del logaritmo: x ≠ 1
Luego la única solución es 2.
El número de soluciones = 1
* Resolver:
2
Log (2x - x + 1) = 2
(-x - 1)
E indicar el conjunto solución.
Resolución:
De la definición:

54. 2 2 2
log (2x - x + 1) = 2 ↔ (-x -1) = 2x - x + 1
(-x-1)
2
Efectuando: 0 = x - 3x
Ahora tenemos que: x = 0 v x = 3
Pero base de logaritmo = - x - 1 > 0
Luego, no hay solución. Ec. Incompatible.
RELACIÓN FUNDAMENTAL m m
5ta. log a = log a
bn n b
c
b = a ................ (1) m m
Log a = c................ (2) Si a = b: log b =
bn n
b
n
Reemplazando (2) en (1): 6ta. log a = log a
b bn
log a
b b =a
logbc logba
7ma. a =c
Ejemplos: calcular cada caso:
lo g 3 lo g 3
4 (x -2 ) CAMBIO DE BASE
• 4 = 3 • (x - 2 ) =
lo g 4 log x a
lo g 4 (2 x) log a = x > 0; x ≠ 1
5 b
• 5 = 4 • (2 x) = log x b
• Resolver:
1
Si x = a: log a =
logx3x-2 b
x = 27 log a b
Resolución:
log 3x-2 REGLA DE LA CADENA
Tenemos que: x x = 27
x-2 3
Entonces: 3 =3 log a . log b . log c . log d = log a
b c d e e
Luego: x-2=3
x=5 DEFINICIONES
• Resolver:
4 -3x Logaritmo Decimal: Llamado también
lo g 3 logaritmo vulgar o de Briggs, su base es 10.
4
lo g 4 = - 8
3 loga = log a
10
Resolución:
Ejemplo:
log 4 34-3x
log 4 = -8 4
3 * log10 000 = log 10 = 4
10
4-3x
log 3 = -8 -1
3 * log(1/10) = log 10 = -1
10
4 - 3x = - 8 → x = 4
Logaritmo Neperiano: Llamado también
PROPIEDADES OPERATIVAS
logaritmo natural, su base es "e" (número de
Neper) cuyo valor es e = 2,718281...
1ra. log b = 1 ; log 1 = 0
b b Lnx = log x ; x > 0
e
2da. log A + log B = log (AB)
b b b Cologaritmo (Colog)
-1
Colog x = log x ; x >0 b>0;b≠1
3ra. log A - log B = log (A/B) b b
b b b
Antilogaritmo (Antilog)
n
4ta. nlog A = log A x
b b Antilog x = b ; x ∈ IR, b > 0 ; b ≠ 1
b
Con la propiedad:

55. Logaritmos Cuarto Año
Antilog log x = x
b b
ejercicioS DeSarrollaDoS
E = log 3. log 12 - log 3 + log 12
2 6 2 6
1. Calcular:
E = log 3 (log 12 - 1) + log 12
2 6 6
M = 3loga x + 7 x loga 3 E = log 3 (log 12 - log 6) + log 12
2 6 6 6
log32 E = log 3 . log 2 + log 12
Si se sabe que: x = 2 ;a=2 2 6 6
Resolución: E = log 3 + log 12 = log 36 = 2
Reemplaza el valor de "a"; aplicamos P.7. 6 6 6
M= x log2 3 + 7 x log2 3 4. Efectuar:
-1 2 3
(1+log xy + log x ) log x
M = 8 x log2 3 x2 y2 x3y3
Ahora reemplazamos el valor de "x" en M. Resolución:
1
M = 8.(2log3 2 )log2 3 2
= (log x + log xy + ) log x
3
x2 x2 log y2
x2 x3y3
M = 8.2log3 2.log2 3 2 2 3
Por la regla de la cadena: = (log x + log xy + log y ) log x
x2 x2 x2 x3y3
M = 8.2 = 4
3 3 3 3 3
= (log x y ) . log x = log x =
2. Hallar "x" en: x2 x3y3 x2 2
x.log2 + log(log2) = log(log16)
Resolución: 10
En el primer término aplicamos: P.4. 5. Si: x =
3 . Halle n de:
x log x
log2 + log(log2) = log(log16) ( x n )log x 3 = 3 3
+ 21+ 4 log 4 x
Tenemos una suma de logaritmos aplicamos
P.2. Resolución:
2
x x n log x 3 = 3log3 x + 21.2 4 log4 x
log(2 .log2) = log(log16)
x
Comparando: 2 . log2 = log16 log 3n
x
2 . log 2 = log2
4 x x = x 2 + 2.2 4 log2 x
Aplicamos: P.4. log 2 x 2
3n = x 2 + 2.2
x
2 . log2 = 4log2
3n = x 2 + 2 x 2 ⇒ 3n = 3 x 2
x
2 =4 ⇒ x=2 Reemplazando el valor de "x".
1
10 2
3. Calcular: n
3 = 3. 3 ⇒3 = n
3.3 5
1 1
E = log 3. log 12 -
2 6 + 6
6
log 3 2 log12 6 n
3 = 3 5 ∴n=
Resolución: 5
1 1
E = log 3. log 12 -
2 6 +
log 3 2 log12 6
ejercicioS para la claSe
1. Calcular: M = 2log25 + 10log3 - log264 a) 3 b) -2 c) 2
d) 5 e)

56. d) 1 - a + 2b e) 2 + a
2 log62
2. Calcular: H = log33 + 36 + log 125
5 Ln( x 2 −11 )
a) 9 b) 8 c) 6 14. Resolver: e = 9 x − 29
d) 5 e) 3 a) 9 b) 3 c) 2
3. Calcular "x": log3(2x - 1) = 2 d) 6 e) 4
a) 6 b) 5 c) 8
d) -5 e) 3 15. Hallar "x".
2 1
logx + 3 log x - logx = log 81
4. Hallar el valor de "x" en: 3 6
log (x - 1) = log 3 + log 4 a) 3 b) 9 c) 1/9
2 2 2
a) 6 b) 12 c) 13 d) 1/3 e) 27
d) 8 e) -13
5. Calcular el valor de "x" en:
log (3x - 5) = log 18 - log 9
3 3 3 16. Resolver:
a) 2/3 b) 7/3 c) 1/3
d) 3 e) -2/3 log( x 2 + 7 x − 5)
=2
log( x + 3)
6. Calcular el valor de "x" en: a) 8 b) 13 c) 14/13
log (log (2x - 1)) = 1 d) 14 e) 4
2 3
a) 5 b) 6 c) 7
d) 8 e) 10 17. Reducir: M = 2log log 100 + log log 2 - log log 16
a) 2 b) 1 c) 0
7. Calcular: E = log168 + log8127 + log12525 d) log2 e) log log 2
a) 7/6 b) 13/6 c) 5/6
d) 5/12 e) 2
18. 8. Efectuar:
1 1
+
8. Resolver: (log2x)2 - 5log2x - 24 = 0 1 + log y x 1 + log x y
Indicar el producto de soluciones a) 1 b) -1 c) 0
a) 64 b) 32 c) 16 d) log x e) log y
y x
d) 256 e) 128
19. Resolver:
9. Reducir: H = antilog5(log52 + colog5(log39)) 17
log x + log 27 x + log 9 x =
a) 25 b) 5 c) 1 3 2
d) 1/5 e) 1/25
a) 9 b) 3 c) 3
3
10. Si log2 = a y log3 = b. d) 27 e) 3
Hallar el valor de: log72
a) 3a + 2b b) 6ab c) 4ab 20. Resolver: log3x . log3(9x) = 35
d) 3a + 4b e) 2a + 3b Indique el producto de sus soluciones.
-1 -2 3
11. Indicar el producto de soluciones de la a) 3 b) 3 c) 3
2
2 2 d) 3 e) 3
ecuación: log x - logx - 24 = 0
10 4 2
a) 10 b) 10 c) 10 21. Reducir:
3 5
d) 10 e) 10
3 log 3 3 log 2 3 log
4
64
5 3
25 + 81 + 2
12. Hallar: E = log197 antilog197 23 + colog28 a) 16 b) 25 c) 18
a) 23 b) 26 c) 20 d) 27 e) 32
d) 19 e) 17
22. Si: a3b3 = a + b . Hallar "x" de:
13. Si: log2 = a , log3 = b logabx
(a + b) = 64
Hallar: log48
a) 10 b) 8 c) 6
a) 4a + b b) 4ab c) 1 + 2a

57. Logaritmos Cuarto Año
d) 4 e) 2 Hallar: log2
1 1
23. Calcular: a) (a + 3b - 3) b) (a - 3b + 3)
2 3
1 1 1
M = 9 log 8 ( + log 4 3 2 ) + 6 log 3 8 c) (3b - a - 3) d) (a - 3b + 3)
3 2
3 3
a) 49 b) 12 c) 51 1
d) 38 e) 63 e) (3b - a + 3)
3
24. Reducir:
1 1 28. Efectuar:
+ 3 2 1
2 + log y x 1 + log xy y + +
a) 1 b) 0 c) log xy log 2 45 + 3 log 3 40 + 2 log 5 72 + 1
x
a) 2 b) -1 c) 1
d) log y e) log x
xy xy d) 1/2 e) -1/2
29. Calcular: E = colog6 antilog3 (log312 + 1)
25. Revolver: Ln(2x) . loge . log 10 = 3
x a) 1/2 b) 2 c) -2
a) 2 b) 2 c) 4 d) 1/4 e) -1/2
d) 1/2 e) 4
2
k + 1 Calcular:
30. Si: a =
k
26. Reducir: E = log0,25antilog64colog8(1/2) k
log a + log a + log a + . . . + log a
a) 1 b) -1 c) 1/2 b 1 b 2 b 3 b 99
d) -1/4 e) 1/4 4/7
donde: = 10
a) 3 b) 2 c) 3,5
27. Si: log27 = a ∧ log 15 = b d) 4 e) 2,5
Tarea Domiciliaria
1. Calcular: log 36 + log 81 + log 0,25
6 3 2 1 1
+
1 + 2 log 4 3 1 + 2 log 9 2
log58 log35 log9
2. Calcular: E = 25 -3 + 100
9. Calcular:
3. Si: log9 = a, log6 = b ; Hallar: log 8 F = co log 4 anti log 4 (2 + log 4 3)
3
4. Resolver: 10. Efectuar: antilog
3
colog 63 +
3
 x colog 9
3logx - log32 = 2log   363
2
11. Calcular:
5. Resolver: (logx)2 - 7logx + 12 = 0 A=9
log 2 5. log 3 2
+4
log 11 3. log 2 11
E indicar el producto de soluciones:
12. Resolver:
6. Si: log2 = x, log3 = y log( 35 − x 3 )
Hallar: log 144
=3
log( 5 − x )
E indicar la mayor solución.
7. Si:
2 3 n 6
Log 4 + log 4 + log 4 + ... + log 4 = log 4 13. Resolver:
2 2 2 2 2
El valor de "n" es: log 2
(log 2 ( x − 1)) = 4
8. Reducir: 0
14. Resolver: log (3 + log x) = 4
2x 2
Indique la solución.

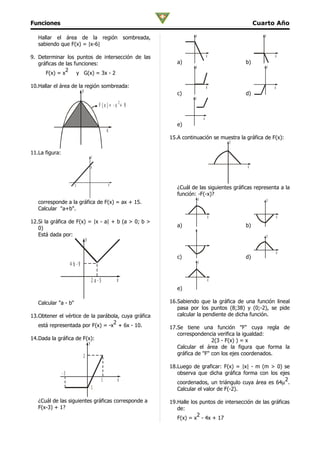
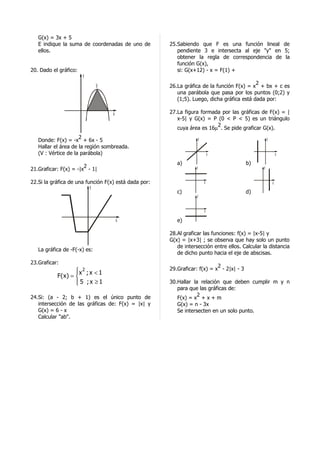
58. 23. Indicar el producto de soluciones de:
15. Si: (m+n)4 = m.n 2log x - 12log 9 = 5
9 x
4logmnx2
(m + n) = 4; (x > 0)
24. Si: log2 = a ∧ log 3 = b
16. Reducir: Hallar: log 60
6
3 3
+ 25. Resolver:
2 + log 2 6 1 + log 12 2
log x −1 (2 x 2 − 8 x +17 )
x −1 = x +1
17. Reducir:
E indicar el producto de soluciones
M = (logx xy + 1)(logx 2 y y + 1) log x
( xy )2
16 + 8 log 2 x = log 2 x − 4
18. Calcular: colog antilog (log 12 + 1)
6 3 3
26. Resolver:
19. Obtener: E = log antilog log log (512) a+b 1
2 2 3 2  2  = 2 [log a + log b]
log  
27. Si:  
20. Resolver: antilog (log (Lnx) + log9) = 18 2 2
a + b = xab, el valor de "x" es.
2 28. Calcular:
21. Resolver: log (x + 7x) = 3
2
3
E indique la suma de sus soluciones. A = log antilog colog 0,25 - 2log2 + Lne - 2
log 2 3
log 32
log 9 5 5 29. Hallar "x" en:
22. Calcular: E=4 colog (1 + log (x-1) ) = log 4
3 2 1/2
ejercicioS para la claSe
1. Calcular: log3(2 - x) 2
3 = x - 2x - 4
log 2 5 3 a) 3 b) -2 c) -6
2 + log 6 6
H= d) 2 e) -1
log 3 3
a) 16 b) 18 c) 25 6. El valor de "x" en la ecuación:
d) 27 e) 9 logx81
3 = x es:
a) 1 b) 3 c) 1/2
2. 2. Calcular el valor de: d) 1/9 e) 1/27
M = log 10 + log 3 3 − log 5 5
7. Si log 9 = a , log 6 = b ;
a) 2 b) 0 c) 3 Calcular el logaritmo vulgar de 25
d) -1 e) 1/2 a) a + 2b - 2 b) a - 2b + 1
c) a + 2b - 1 d) a - 2b + 2
3. Calcular el valor de "x" en: e) 2a - 2b + 2
log (5x + 1) = 4
3
a) 15 b) -15 c) 16 8. Resolver: 8 + log3(4log3x) = log3(36log3x)
d) 20 e) 17
a) 27 b) 9 c) 81
4. Calcular "x" en: d) 16 e) 144
x = log 7 3 ( l og 3 7
) 9. Sea: f(x) = log3x
a) 1 b) 0 c) -1 Hallar el valor de "x" en:
d) 1/2 e) 3/2 f(81) - f(x) = f(x) - 2f(3)
a) 81 b) 27 c) 3
5. Resolver e indicar el producto de soluciones d) 1/3 e) 9
en:

59. Logaritmos Cuarto Año
10. Sean:
3 g(x) = log 1 x 19. Resolver: 2log(logx) = log(7-2logx) -
f (x) = + log 9 x log5
2 y 8
a) 3 b) 5 c) -3;5
Calcular: E = g(f(243)) d) 10 e) 8
a) 3/2 b)-2/3 c) -1/4
20. Resolver la ecuación:
d) -1 e) -1/2
x + log (1 + 2x) = xlog5 + log 6
Hallar: x + 1
11. Halle "x" que verifica: a) 0 b) 1 c) 2
log 2 n = log 2 (log x n) d) 3 e) 8
a) n
n
b) n c) n a log 9 x
n 21. Si: x =4
n n-1
d) e) n Hallar el logaritmo de 6 en base 2.
a 1 a +1
x
12. Halle: x si: a) a +1 b) a + 1 c) a
Log7.Lnx d) a+1 e) 2a
Log e = Log(Lnx)
7
e → número de NÉPER 22. Efectuar:
2 -1
a) e b) e c) e 1 1
e E= − + log x y + 1
10 e 1 − log xy x 1 − log xy y
d) e e)
a) log xy b) log x c) log xy
x y y
13. Hallar "x" de: d) log x e) 1
22 xy
(Antilog Log Antilog (Log 4) )
3 4 3 3
a) 8 b) 16 c) 64 23. Calcular "x" de:
d) 128 e) 1024 log 2 a
a x
+ log ax a. log1 / a (2 x ) = 0
14. Resolver: log 2 x a
2 2
log (x-4)+log 2 = log (5x - 16x - 12) - 1 a) a b) a c) a
3 3 3
a) 2 b) 6 c) 4 4
a 4
d) 8 e) Hay 2 respuestas d) e) a
15. Resolver: 24. Si: logxyx2 = 2a
log log(x - 5) + log2 = log log (x + 1)
Donde x > y son enteros consecutivos.
e indicar la suma de soluciones.
Hallar: Log y
a) 11 b) 12 c) 24 xy
d) 8 e) 10 a) 1+a b) 1-a c) 1-2a
a a
16. Resolver: 5log x - 3log x = 28 d) 1+ e) 1-
2 4 2 2
a) 64 b) 128 c) 256  p+q
d) 512 e) 1024 25. Si: 10x + 10y = p ; x - y = log 
 p−q

 
1 x y
17. Resolver: 3log x - =8log 2 Hallar: 10 - 10
2 log 2 x
x  p+q
Indicar una solución entera. a) 
 
 b) p - q c) q
a) 1 b) 2 c) 3  p−q
d) 4 e) 5 d) 2q e) logp - logq
18. Resolver: log 12 - 3log 4 + log 6 = 4
x x2 x
26. Luego de resolver la siguiente ecuación:
log 2 - log 2 = log 2
x x/16 x/64
a) 3 b) -
3 c) ± 3 Indicar el producto de sus soluciones.
d) 2 e) -1 a) 12 b) 17 c) 1

60. d) 16 e) 24 a) 1 b) 3 c) 2
d) 1/2 e) -1
27. Calcular "x" en:
log x 29. Si "x" e "y" son valores que satisfacen el
x1−Inx = e 5 sistema:
log e 5In 10 5 log e
 10   e   10  e x = y e ..........
 .......... (1)
......
 5
   
 10   
 e  
a)  e  b)   c)   4 x = e(4 + Ln 2 y ) .......... 2)
 ...(
In10
 e5   10 
In10 donde "e" es el número de NEPER, halle "xy".
   5 2 3
 10    a) 3e b) 3e c) 2e
d)   e)  e  5
d) 2e e) 4e
28. Sabiendo que "x", "y", "z" verifican:
1 1 1 30. El valor absoluto de la diferencia de las
+ =
x−y y−z x−z soluciones de la ecuación:
−2 log 5 x
Hallar: 1  1 
5  + x log 2   = − log 3 81
log( x − y ) + log( y − z)    32 
log( x − z) a) 6 b) 5 c) 4
d) 3 e) 2
Tarea Domiciliaria
5 2
1. Hallar "x" Si: log x + log x =28
3 3
6. Si se sabe que:
log 15 (15 x 2 −2 x + 7 ) log 14 (14 x 2 −2 x +7 )
2. Resolver: 225 − 196 =0
log 1 (x − 1) − log 1 (x + 3) = 1 Dar como respuesta el mayor valor de "x".
2 2
7. Hallar el valor de "x" en:
3. Si: Lognm = 2 ∧ Logmp = 3
log( x + 1 + 1)
3
=3
2 4 log x − 40
Calcular: log (m p )
n3
8. Resolver la ecuación:
4. Resolver: log 5 (2 x 2 −13 x +19 ) log 5 169
13 =2
3 1
log 2 x + log 2 ( x − 2) = 1 y calcular el producto de las soluciones.
3
y dar como respuesta la suma de las
50 2
soluciones. 2 2
9. El logaritmo de en base es "y"
Calcular: log 5+log 10+y
50 10y
5. Dada la ecuación:
e x − 4e − x
y= 10. Resolver:
2
log 3.log 4.log 5 ...log 2002 log x = log 2002
Encontrar "x", para y = 1,5. 2 3 4 2001 y 2003

61. Logaritmos Cuarto Año
Calcular la suma de cifras de: (x + y + 2003)
19. Resolver el sistema y dar el valor de "y":
11. Resolver: log(log5 8)
  log5 8 − 1
(log x 2) log x 2  = log x 2
 
 16  64
Indicar la suma de soluciones. 20. Resolver la ecuación:
log 2 x 2 log a x
12. Hallar el valor de "x" en: − = log a
x − log a x
log 2 a log 1 a
1 + log2 (x + 4) x
=1
log 2
( x + 3 + x − 3)
21. Resolver la ecuación:
log ( x 2 −7 x + 21) log 4 x a
13. Resolver: 2
7 =3 7 4 4
log a ax + log x ax + log a 4 + log x 4 =a
a x
Indicar una solución.
14. Del sistema adjunto, proporcionar: logxy 22. Resolver:
log a log b logx logx2 logx3 logxx x2+x
a .x=b . y ... (1) (logb) .(logb) (logb) ...(logb) = (logb)
log b log a
b .x=a . y ... (2)
23. ¿Qué valor de "x" verifica la igualdad
anti log 4 x = anti log 2 [co log 6
(3 log 3
3)]
15. Si "e" representa la base de logaritmos
neperianos, resolver (L = Ln)
log x 24. Hallar el valor de "a" en la siguiente
 Lx − e  1
log x 
 Lx + e 
 =L 
e expresión:
   
( )
a a a
16. Si: x = logb . antilogb . cologb . antilogb(- log a
aa .loga a a .loga a= 3
a
-1
b ) Calcular:
10
3
( )
2
logb 2 x + cologx b  + colog 1 bx + b
x −2 2 25. Calcular "E", si: x =

 

x
 log x
log 2 x log x 
17. Resolver la siguiente ecuación: E = log x  3 3
+4 +6 6 
 
 
3 log(log x )
log [log(log x )]
log(log x) = 27
26. Resolver el sistema. Hallar "x".
2 2
18. Hallar el valor de "x" en el siguiente sistema log xy - log = 8 . . . (1)
y x x y logx logy
de ecuaciones: x = y ; 8 = 5 2 =4 ……...... . (2)

62. log2 log5
(2x) = (5y)
27. . Si se verifican las ecuaciones, hallar "xy"
logx logy
5 =2

63. Ecuaciones con Valor Absoluto Cuarto Año
Tema nº 04: ecuacioneS con valor abSoluTo
Capacidades:
 Resuelve ecuaciones con valor absoluto.
Desarrollo del Tema:
Definición: ejemplo:
 x ; x≥0
| x |= 
− x ; x < 0
3
2 43 3
(
  = − 2 − 3
− 
4
)
−
Propiedades:
1) |x| ≥ 0 ; ∀ x ∈ R
2) |xy| = |x| |y| ∀ x , y ∈ R
x |x|
3) = ; y≠0
y |y|
4) |x|2 = x2
5) |x| = |-x|
n
6) x = n| x |
ECUACIONES CON VALOR ABSOLUTO
| x |= a ↔ a ≥ 0 ∧ ( x = a ∨ x = −a)
| x |=| y |↔ x = y ∨ x = − y
Ejemplo:
IV III II I
-1 2 3
1) |2x + 1| = 5x + 3
5 x + 3 ≥ 0 ∧ (2x + 1 = 5 x + 3 ∨ 2x + 1 = −(5 x + 3))
En I: x–3+x+1=x–2
3  2 4 x>3 ∧ x=0
x ≥ − ∧ x = − ∨ x = − 
5  3 7 ⇒ No hay solución
4
C.S. =   En II: -x + 3 +x + 1 = x – 2
7 
2< x < 3 ∧ 6=x
⇒ No hay solución
2) |2x2 – 2x + 5| = |x2 + 2|
En III: -x + 3 + x +1 = -x + 2
⇒ 2x 2 − 2x + 5 = x 2 + 2 ∨ 2x 2 − 2x + 5 = − x 2 − 2 -1 < x < 2 x = -2
x 2 − 2x + 3 = 0 ∨ 3 x 2 − 2x + 7 = 0 ⇒ No cumple
x∈ C x∈ C
∴ C.S. ∈ C En IV: -x + 3 – x – 1 = -x + 2
0=x
⇒ No cumple.
3) |x – 3| + |x + 1| = |x – 2|
∴ C.S. = ∅

64. problemaS para la claSe
Resolver los siguientes casos: (Hallar el y +=
3 6
conjunto solución) 13)
1) |x – 2| = 5 f + 6
14) 4
=7
2) |3x – 5| = -2
3) |3x – 1| = x 15) 5r − = +
4 3r 8
4) |x – 8| = 3
16) 4 g −2 = g +13
5) |2x – 3| = 7
6) |3x – 5| = 2x 17) 5 − 3k − 2 = 2k
7) |6x – 8| = 2
18) 8m − = m −
3 3 2
8) |2x – 9| = x + 2
9) |x – 8| = 2x 6z + = − z
1 5 4
19)
10) |x2 – 5x| = |6|
3d −5
11)|x – 2| = - 5 20) 2
= −
d 1
4x − 1
12) = 2x
3
problemaS para la caSa
Hallar el conjunto solución: c) {3/2 ; 3} d) {6 ; 8} e)
N.A.
1) |x – 5| = 3
a) {8 ; 2} b) {8 ; 0} c) 7) |x2 – |x – 2|| = x – 1
{6 ; 1} a) C.S. = {1 ; -1 ; 3}
d) {3 ; 4} e) N.A. b) C.S. = {2 ; -3 ; 1}
c) C.S. = {1 ; -2 ; 9}
2) |2x – 3| = 5 d) C.S. = {1 ; -1 ; 4}
a) {-4 ; -1} b) {4 ; -1} e) N.A.
c) {3 ; -1} d) {5 ; -2} e)
N.A. 8) |3 – |x|| = 2
a) C.S. = {-2 ; 1 ; 3 ; 0}
3) |5x – 6| = -2 b) C.S. = {-3 ; 2 ; 1}
a) {4/5 ; 8/5} b) {4 ; 8/5} c) C.S. = {-5 ; -1 ; 1 ; 5}
c) {4 ; 9} d) {4/3 ; 8/3} d) C.S. = {-2 ; 1 ; 5 ; 9}
e) N.A.
e) N.A.
9) Resolver: 5 x −3 = 4 x +1
4) |2x – 7| = 13
a) {10 ; 3} b) {-3 ; 5} A) 4 B) 2/9 C)4
c) {10 ; -3} d) {-3 ; 9} e) ó 2/9
N.A. D)-4 ó -2/9 E) -4
5) |6x – 2| = 2x
a) {5 ; 9} b) {1 ; 4} 10) Resolver: x 2 −4 = 3x
c) {1/8 ; 3/4} d) {1/2 ; 1/4} e) A) -1 B) 4 C)1
{2 ; 4} ó4
D)-1 ó 4 E) C ∪D
6) |7x – 9| = |x|
a) {3/2 ; 9/8} b) {3 ; 8}

65. Ecuaciones con Valor Absoluto Cuarto Año
3x + 1 1 7  1 1 
11) Resolver: =4 D)  ;  E)  ; 
x −1
4 3 3 7 
A) 4 B) -3/7 C)5 ó
3/7
D)-5 ó 3/7 E) N.A. 19) Resuelva:
( x − 3) 2 − 9 x − 3 + 20 = 0
Dando como respuesta la suma de los
12) Resolver: x 2 + x −20 = 0
elementos de su conjunto solución.
A) 5 y -4 B)4 y -4 C)5 y
-5 A) 10 B) 12 C)4
D)-5 y 4 E) -4 D)6 E)9
13) Resolver: x −2 = 4 20) Resuelva x − 1 + x − 1 = x − 1
Siendo la solución: C.S . = { − a; b} A) {1;−1} B) { 0;−1} C)
Calcular: a + b
{ 2;1}
D) { − 1;−2} E) { 0;1}
A) -6 B) 8 C)-4
D)0 E)4 21) Resuelva x2 +1 − x = x
14) Resolver: x + 5 = 2x − 4 , e indicar la A) {1;−1 + 2;1 + 2} B) {1; 2 }
suma de las raíces obtenidas. C) {1;1 + 2 } D) {− 1;+ 2 }
E) {− 1 + 2 ;1 + 2 }
1
A) 26/3 B) 28/3 C) 9
3
D)9 E)-1/3
2x − 5 + 2x + 1 = 2(x + 5)
22) Resolver: ;
15)Dadas las ecuaciones: hallar el menor valor de "x".
I. 3x − 5 + x − 7 = 0 a)-2 b)-5 c) -3 d)2 e)5
II. x 2 + 2 = 2x + 1 2(x + 1) − 2 = 8
23) Resolver: ; hallar la suma
Calcular la suma de todas las raíces de valores de "x".
a)-2 b)-1 c) 0d) 1 e) 16
que se obtienen de I y II
A) 5 B) 3 C)9 x−5 +3= x−5 +8
D)2 E)4 24) Resolver: 2 ; hallar el
producto de valores de "x".
16) Determinar el numero de soluciones de a) 50 b) -50 c) 10 d) 5 e) 0
la ecuación x − 1 = 2003
3 x+5 −2 x+5 = 8
A) 5 B) 3 C)1 25) Resolver: ; hallar
D)2 E)4 el mayor valor de "x".
a) 3 b) 4 c) 5 d)6 e)7
2
17) Resuelva x + 2 − 1 − 5 x + 2 − 1 − 6 = 0
3x − 5 = 2x + 15
A) { 3;2} B) { 5;−9} C) { 5;9}
26) Resolver:
valor de "x".
Hallar un
D) { − 5;9} E) { − 1;5} a) 5 b)-2 c) 10 d) -20 e) -10
2x + 3 = x − 12
18) Resuelva 2 x + 3 + 4 = 5x 27) Resolver: , hallar el
producto de valores de "x".
1 3  7 
A) {1;3} B)  ;  C)  
7 7  3 a) 35 b) -45 c) -35 d) 15
e) -75

66. x + −5 = − 8  1
28) Si: ; e) − 3,−5, 
y + a − 3 = 12  3
Además
¿Indique el mayor valor que puede tener "y"? 37)Las soluciones de la ecuación :
a) -1 b) 15 c) 12 d) 20 e)18
18 − 3x − x 2 = 3 − x son :
29) Indique la suma de valores de: "x+y" a) –5 y 3 b) –7 y –5 c) –6 y 2
si se cumple que: d) –5; -7 y 3 e) –5; -6 y 3
x+1 + 3 =8
y−1 + 2 =7 2
38) Resolver: 3 x − 3 − 14 x − 3 − 5 = 0
a) 0 b) 20 c) -20 d) -12
e) 8 a) { − 2,2} b) { − 3,4} c) { − 2,8}
d) { − 5,3} e) { − 3,1}
30) Resolver la siguiente ecuación:
39) Resolver : 3x − 5 = 40 − 6x
2
6+ x = x+9 + x−2 e indique el
a) { − 5,2} b) { − 3,2} c)
número de elementos de su conjunto
solución. { − 5,−3} d) { − 5,3} e) { − 3,5}
a) 0 b) 20 c) 20 d)12
e) 8
40) x −2 −3 = x + 4
31)resolver e indicar el número de
elementos de su conjunto solución. 1 −5
a) b) c)
x2 − 5 x + 6 = 0 2 2
a) 4 b) 2 c) 5 d) 6 e) 8 11 − 5  − 5 1
 ,  d)1 e)  , 
2 2   2 2
32) hallar el conjunto solución de:
3x − 9 + x + 2 = 2 x − 6 + 2 x + 4 41)Después de resolver la ecuación :
a) 1/2 b) -1/2 x − 5 + 3 = 2 ; se puede decir que:
c) 2 d) 12 e) 7
33) hallar la suma de las raíces de la ecuación: solución es x = 5
a) Su
2 b) Su solución es x = 8
2 x − 3 + 7 x − 21 = 15
c) Su solución es x = 0
a) 11/2 b) 6 c) 7 d) 9/2 e) 5
d) Es una ecuación indeterminada
e) Es una ecuación imposible.
34)Resolver :
2
x +2 −1 −5 x +2 −1 −6 = 0 42)Las soluciones de la ecuación :
a) { − 9,5} b) { − 3,2} c) { − 5,9} x +x 3= 0 ; son :
d) { − 5,3} e) { − 8,4} a) –1; 0 b) –2; -1 c) –2; 0
d) –1; 1 e) 0; 1
35) Resolver : x − 3 = 3x + 2
x − 4 + 2 x + 9 = 20
 5 1 43) Resolver:
a) { − 5,2} b) − ,  c) { − 2,3} Dar como respuesta el máximo
 4 4
valor entero del conjunto
d) { − 5,3} e) { − 5,5}
solución
36)Resolver :
a) -2 b) -1 c) 2 d) 1 e) 3
2x + 1 − 3x − 2 + x − 5 = x + 2 2
x − x − 42 = 0
 1 11  2 11 44) Resolver :
a) − 5, ,  b) − 3, , 
 3 3  3 3 Dar la suma de soluciones.
 1 a) 0 b) 1 c) 2 d)3 e) 4
c) − 2,−3,  d) { − 5,3}
 3

67. Ecuaciones con Valor Absoluto Cuarto Año
45)Resolver la ecuación siguiente : Dar la suma de soluciones.
x + x − 12 = 3 − x
2
a) 1 b) 3 c) 5 d) –5 e) -3

68. Tema nº 05: ecuacioneS De graDo Superior
Capacidades:
 Resuelve ecuaciones de grado superior.
Desarrollo del Tema:
Ecuaciones Polinómicas ( x − 1), ( x + 2), x
P( x) = a0 x n + a1 x n −1 + a2 x n −2 + ........ a0 = 0
+
Son ecuaciones de la forma:
a 0 , a1 ,......., n los
a Definición:
Donde: coeficientes ‘‘r’’ es una raíz de multiplicidad "k" de un
( a ≠ 0) . polinomio P(x) si:
n ∈ IN , n ≥ 1 es el grado de la ecuación. P(x) = (x − r)k ⋅ Q(x); Q(r) ≠ 0
k ∈ IN; k ≥ 2
Definición.
‘‘r’’ es una ‘‘raíz’’ o ‘‘cero’’ del polinomio:
Ejemplo:
P( x ) ⇔ P(r ) = 0 Indicar las raíces del polinomio:
P( x ) = ( x + 2) 3 ( x − 1) 6 ( x − 3) x 4
Ejemplo:
e indicar la multiplicidad de dichas
Sea el polinomio:
raíces.
P( x ) = x 3 + 3x 2 − 4 x − 12 = 0 Resolución:
Se observa que: Igualamos cada factor a cero:
Si : x = 2; P(2) = (2) 3 + 3(2) 2 − 4(2) − 12 = 0
P(2) = 0 ( x + 2) 3 = 0 ⇒ ( x + 2)( x + 2)( x + 2) = 0
Entonces x = 2 es una raíz de la ecuación. De donde:
x + 2 = 0 → x = −2
Teorema del factor x + 2 = 0 → x = −2
‘‘r’’ es una ‘‘raíz’’ o ‘‘cero’’ del polinomio
x + 2 = 0 → x = −2
P( x ) ⇔ ( x − r) es factor de P(x).
Ejemplo:
∴ x = −2 es una raíz de multiplicidad 3.
Sean: 1; −2; 0 las raíces o ceros del De igual manera para
polinomio P(x), hallar sus factores. (x − 1)6 = 0 ⇒ x = 1
es una raíz de
Resolución: multiplicidad 6.
1er factor: (x − (1)) = (x − 1)
2do factor: (x − (−2)) = (x + 2)
3er factor: (x − 0) = x ( x − 3) = 0 ⇒ x = 3 es una raíz simple.
Entonces P(x) tendrá como tres de sus x 4 = 0 ⇒ x = 0 es una raíz de multiplici dad 4.
factores:
Método básico de resolución de una ecuación polinómica.
1° Se factoriza.
2° Cada factor se iguala a cero.
Ejemplos: x 2 ( x + 5) + 9( x + 5) = 0
1. Resolver:
3 2
x + 5x + 9x + 45 = 0
( x + 5)( x 2 + 9) = 0
Resolución: Igualando cada factor a cero.
Factorizando: ∗ x + 5 = 0 ⇒ x = −5
∗ x 2 + 9 = 0 ⇒ x 2 = −9
x = ±3i

69. Ecuaciones de Grado Superior Cuarto Año
Las raíces son: −5; 3i; −3i Finalmente las raíces de la ecuación son:
1, −2, 5, −2.
2. Resolver:
x 4 + 20 = 2 x 3 + 15 x 2 + 4 x 3 2
3. Si x es raíz de: x − 4x + 1 = 0
0
Resolución:
Halle:
La ecuación se puede escribir:
4 3 2 x3 + 7
0
x − 2 x − 15 x − 4 x + 20 = 0 E=
2x 2 + 3
0
La factorización no es inmediata, se Resolución:
puede resolver aplicando la regla de Como "x " es raíz debe verificar la
0
Ruffini: ecuación:
1 −2 −15 −4 20 x 3 − 4x 2 + 1 = 0
0 0
x =1 1 −1 − 16 − 20 Despejamos:
1 −1 − 16 − 20 0 x3 :
0
x = −2 −2 −6 20 x 3 = 4x 2 − 1
0 0
1 −3 − 10 0 Reemplazando:
∴ dos raíces son : 1,−2 E=
(4 x 2
0 )
−1 + 7
Notar que se aplicó Ruffini hasta que
2x 2
0 +3
quedaron 3 términos formándose una 4x2 + 6
0
ecuación de 2do grado: E=
2
2x 2 + 3
0
1x − 3x − 10 = 0
( x − 5)( x + 2) = 0 E=
(
2 2x 2 + 3
0 )
2x 2
0 +3
Resolviendo: x= 5 y x = −2
E=2
Teorema de Cardano – Viete
Este Teorema permite encontrar una relación entre las raíces de un polinomio P(x) y sus
coeficientes.
Si: x ; x ; x ; … x son las ‘‘n’’ raíces de la ecuación polinominal:
1 2 3 n
n n−1 n−2
P(x) = a x + a x +a x +…+a x+a =0;a ≠0
0 1 2 n−1 n 0
Entonces se cumple:
Suma de raíces:
a 1
x + x + x + ... + x =
1 2 3 n a 0
Suma de productos binarios de las raíces:
a2
x1x2 + x1x3 + x1x4 + … + xn-1 xn =
a0
Suma de productos ternarios de las raíces:
a3
x1 x 2 x 3 + x1 x 2 x 4 + ... + x n−2 x n−1 x n = −
a0
Producto de las "n" raíces:
an
x 1 x 2 x 3 ...x n = (−1) n
a0

70. Ejemplo: Resolución:
Sean las raíces: x , x , x
1 2 3
1. Para una ecuación de 3° Grado
Forma General: 1 1
+ = x3
Del enunciado: 1
x x2
x 2 + x1
= x3
Si "x ", "x ", "x " son las raíces de la Efectuando:
x1 x 2
1 2 3
ecuación en "x": x +x =x x x
de donde: 2 1 3 1 2
Tenemos que: Sumando "x " para formar la suma de
3
a1
x +x +x = − raíces:
1 2 3
a0 x 2 + x1 + x 3 = x 3 x1 x 2 + x 3
a2 Usamos las propiedades de suma y
x x +x x +x x =
1 2 1 3 2 3 producto de raíces:
a0
−a = −c + x 3
x x x = −
a3 ⇒ Negativo pues el
1 2 3 Despejamos la raíz "x ":
a0 3
grado es impar c − a = x3
2. Para una ecuación de 4to Grado Ejemplos:
Forma General: Sabiendo que la ecuación tiene 4 raíces:
"x ", "x ", "x ", "x "
1 2 3 4
nx 3n−11 + (k − n)x 3 − 2nx 2 + nk = 0
Si "x ", "x ", "x ", "x " son las raíces de Además:
1 2 3 4 1 1 1 1 4
la ecuación en "x", tenemos que: + + + =
a1 x1 x 2 x 3 x 2 x 3 x 4 x1 x 3 x 4 x1 x 2 x 4 5
x +x +x +x = −
1 2 3 4 Hallar "k".
a0
Resolución:
x x + x x + x x + x x + x x + Para que la ecuación presente 4 raíces
1 2 1 3 1 4 2 3 2 4
a2 debe ser de 4to grado:
x x = 3n − 11 = 4
3 4
a0
x x x + x x x + x x x + x x x = n=5
1 2 3 1 2 4 1 3 4 2 3 4 Reemplazando:
a
− 3 5 x 4 + (k − 5) x 3 − 10 x 2 + 5k = 0
a0 De la condición operando se obtiene:
a
x x x x = + 4 ⇒ Positivo pues el x 4 + x1 + x 2 + x 3 4
1 2 3 4 =
a0 x1 ⋅ x 2 ⋅ x 3 ⋅ x 4 5
grado es par.
Reemplazamos la suma y producto de
Ejemplo: raíces:
4 2 − (k − 5 )
En la ecuación: x + ax + bx + c = 0
5 4
La suma de inversas de dos de sus raíces =
es igual a la tercera raíz. Indicar una de 5k 5
ellas. 2
Resolviendo: k = 1.
ejercicioS para la claSe
1. Resolver:
3 2
2x + x = 15x Si tiene raíces:
x1 < x 2 < x 3

71. Ecuaciones de Grado Superior Cuarto Año
x1 + x 2
8. Sea: "x " , "x " , "x " y "x " raíces de:
x3 1 2 3 4
Indicar:
a) 1 b) -5/6 c) -6/5 3x 4 − 4 x 3 + 5 x 2 + 9 x + 7 = 0
d) -2/185 e) -10/3 Calcular:
E = x 1 + x 2 + x 3 + x 4 + x1 x 2 x 3 x 4
2. Resolver: a) −3 b) -8/3 c) 7/3
2 2 2
(x - 9)(x - 3x) - 10(x - 9) = 0 d) 11/3 e) −1
si sus raíces son: x < x < x < x
1 2 3 4
4 3 2
x x + x2x4 9. Resolver: x - 2x - 7x + 8x + 12 = 0
Halle: 1 3
si tiene raíces:
x1 < x 2 < x 3 < x 4
a) −21 b) 9 c) −19
d) 30 e) 28
Indicar:
x1 x 2 + x1 + x 3 + x 4 x 3
3. Indicar la suma de los cuadrados de los a) 7 b) 8 c) 9
ceros no racionales de la ecuación: d) 11 e) 12
x 3 + 2x 2 − 7 x − 2 = 0
3 2
a) 14 b) 13 c) 10 10. Si la ecuación: 2x + 7x - 3x - 3 = 0
d) 5 e) 2 tiene una raíz racional. Indique la suma
de sus raíces irracionales.
4. Si: "x " y "x " son las raíces de la a) 3/2 b) −3 c) 3
2 3 d) -3/2 e) 1/2
3 2
ecuación: 2 x + 3x − 23 x − 12 = 0
11. Si una raíz de la ecuación:
Además:
x1 < x 2 < x 3
mx 3 + nx 2 + mx + n = 0
x − 2x 2 + x 3
Calcular: 1 (m ⋅ n ≠ 0)
a) 0 b) 2 c) 1
d) −2 e) −1 es: x = −3
1
5. Siendo "x ", "x " y "x " raíces de la -1
1 2 3 Calcular: E = m . n + 1
3 2 a) 1/3 b) 4/3 c) 3/4
ecuación: 3x - 2x + 7x + k = 0
d) 1 e) 4
1 1 1 8
+ + =
x x x 2 x 3 x1 x 3 7 12. Si "x " es una raíz de la ecuación:
Además: 1 2 0
Hallar "k" 5
a) 7/4 b) -7/4 c) 1 x - 3 = 4x
d) -1 e) 1/4 Hallar el valor de:
2x 5 − 5
0
6. Sea la ecuación: 8x 0 + 1
x 3 + (k − 3) x 2 + nx + (2k − 1) = 0 a) 1/2 b) 2/3 c) -3/5
de raíces "x ", "x ", "x "; si: d) −4 e) 1
1 2 3
1 1 1 1 2 2 2
+ + = 13. Resolver: (x + 2) = 6x + 3
x1 x 2 x 2 x 3 x1 x 3 7
e indicar su mayor solución.
Halle "k" a) -3 b) 4 c) 1
a) 5 b) 4 c) 3 d) 3 e) 16
d) 7 e) 26/9
14. La ecuación:
7. La ecuación: n+3 n+2
n- 1 2 2x - (n + 1)x + nx + 5 = 0
(n + 1)x + 7x - 2nx + 3n = 0 tiene 7 raíces. Hallar la suma de estas.
tiene tres raíces x ; x ; x a) 1,5 b) −2,5 c) 4,5
1 2 3
d) 2,5 e) −4
Halle:
E = x1 + x 2 + x 3 + x1 x 2 x 3
a) -1/5 b)-19/5 c)-1 3 2
15. Sea: P(x) = 9x - 36x + 44x - 16
d) -17/5 e) -2
Hallar la mayor de las raíces.

72. a) 2 b) 3 c) 2/3 23. Si: x , x y x son las raíces de la
1 2 3
d) 4 e) 4/3
ecuación: x 4 + 7x − 5 = 0
26. Para que en la siguiente ecuación: Calcular:
3x 5 + 8 x 4 + x + m = 0 3 5 5 5
x1 − + x3 −
2 + x3 −
3
El producto de sus raíces sea igual a la x1 x2 x3
suma de coeficientes de la ecuación, "m"
a) 0 b) −7 c) −14
debe tomar el valor de:
d) −21 e) 10
a) −3 b) −9 c) −12
24. Determinar el valor de ‘‘m’’ si las raíces
d) 7 e) 12
de la ecuación cúbica:
27. En la ecuación cúbica: x 2n−5 − (4n − 1) x 2 + mx + 5 = 0
x 3 + ax 2 + bx + c = 0 Están en progresión aritmética.
a) 16 b) 25 c) 36
se sabe que la suma de las inversas de
d) 49 e) 64
dos de sus raíces es igual a la tercera,
luego una raíz es:
2
a) b − a b) c − b c) c − a 25. Calcular (a + b) , si la ecuación:
d) a − b e) b − c 3 2
x − 14x + 72x − ab = 0
tiene sus raíces proporcionales a 1, 2 y 4.
28. Calcular la suma de las once raíces que
a) 64 b) 100 c) 225
presenta la ecuación polinomial:
d) 81 e) 121
4 x 2n+3 + 3x 2n−7 + 4 = 0
a) -3/2 b) -2/3 c) -1/2 26. Si una raíz de la ecuación:
d) -1 e) 0 3 2
x - 12x + 39x - n = 0
Es la semisuma de las otras dos.
29. Sea "a", "b" y "c" raíces de la ecuación:
3 Calcular:
E = n−3
2x - x + 5 = 0
a) 6 b) 5 c) 4
b3 + 1
E= d) 3 e) 1
Calcular: b−3 27. Sea la ecuación:
a) 1/2 b) 2 c) c 2 x 3 − 5x 2 = 5x − 1
d) -3/2 e) 3
Cuyas raíces son: −1; α; β
Resolver:
3
20. Dada la ecuación: x + ax - 5 = 0
α2 β2
con a ∈ IR cuyas raíces son "x ", "x " y "x
1 2 3 +
6α − 1 6β − 1
Calcular la suma de cubos de dichas
raíces. a) 1 b) 2 c) −3
a) -3 b) -15 c) 9 d) 4 e) −2
d) 15 e) 18
28. Si: α es una raíz de la ecuación:
4 3 2 2
x = -x - 1 y β es una raíz de la
21. La ecuación: x + 9 x + 18 = x + 11x
5
Tiene como una de sus raíces: ecuación: x = x + 2
a) -2 b) 1 c) 3 5 3
Indicar el valor de: β − α β + 2
d) 9 e) 6 a) 1 b) 2 c) 3
d) 4 e) 5
22. Resolver la ecuación:
2 x 3 + 9 x 2 + 10 x + b = 0 x1 = 3 − 2 3; x 2 = −3;
29. Si: "x "
si las raíces son proporcionales a 1, 2, 6. 3
2 son raíces de la ecuación:
Calcular: b − 1.
3 2
a) 1 b) 3 c) 8 x + ax + bx + c = 0
d) 15 e) 24
Determinar:
(a − x 3 )
si: c = 4 3 − 6

73. Ecuaciones de Grado Superior Cuarto Año
4 30. Calcular el valor de ‘‘m’’, sabiendo que
2 3+ las raíces de:
a) 3 b) − 8 − 2 2 3 2
4x - 24x + mx + 18 = 0
Son:
c) − 9 + 3 d)
2 3 x1 = α + β
4 x2 = α
−2 3
e) 3 x3 = α − β
a) 18 b) 21 c) 23
d) 25 e) 27
Tarea Domiciliaria
3 2 Presenta por raíces: "x "; "x "; "x ", y
1. Al resolver: x = 3x + 4x 1 2 3
Se obtiene las raíces "x ”; "x ”; "x ", además: x + x = 0,
1 2 3 1 2
que cumplen que: x >x .
1 2
x <x <x Calcular: (x + x )x
1 2 3. 1 3 2. Calcular: (x + 3x − x )
1 3 2
2. Resolver:
7. Se tiene la ecuación:
( x 2 − 16)( x 2 + 5 x ) + 4( x 2 − 16) = 0 x n − 4 x 3 + 7x + n = 0
cuyas únicas raíces son:
Si sus raíces son: x = x < x < x
1 2 3 4. x 1 = a + 2n
Halle:
x 2 = −a − n
x1 + x 4
x2 + x3 x 3 = 2a − n
x 4 = −a
1. Sea la ecuación: Calcular: ‘‘a’’.
3 2
x - (2n + 1)x + (7n + 2)x - 6n = 0
de raíces: "x ", "x ", "x " que cumple: 8. Sea la ecuación:
1 2 3
5 4 3
1 1 1 9 x - (5 + n)x - (3 - 2n)x + n + 1 = 0
+ + = que presenta a una de sus raíces: x = 1
1
x 1 x 2 x 2 x 3 x 1 x 3 24
Calcular: 5 + n.
Calcular "n" 9. Calcular la menor raíz de:
2 2 2 2 x 3 + x 2 − 13 x + 6 = 0
4. Resolver: (x − 1) = 8(x − 1)
e indicar la menor raíz de la ecuación.
10. Sea la ecuación:
n+4 n+2
5. Sea la ecuación: 4x - 2x -x-8=0
3 2 2 Cuyas raíces únicas son "x ", "x ", "x "
5x - (3m - 1)x - px + 5n - 6 = 0 1 2 3
de raíces: y "x ".
4
x1 = −n Calcular:
1 F=x +x +x +x +x .x .x .x
x2 = − 1 2 3 4 1 2 3 4
5
x 3 = 13 11. Se tiene la ecuación:
n 2
Calcular la suma de valores que toma ‘‘n’’. x - (k - 6)x - (k + 3)x + n = 0
de raíces "x ", "x ", "x " únicas.
1 2 3
3 2
6. Si se cumple que: 3x - x - 12x + 4 = 0 Calcular ‘‘k’’ si la suma de raíces es igual
al producto de ellas.
12. Sea la ecuación:

74. 4 3 2 2
x - (n - 3)x - (n - 1)x + (2n - 7)x + 2 = 0 9 + 4x 0
de raíces "x "; "x "; "x " y "x " que 3 2
1 2 3 4 x0 − x0
verifican que:
x + x + x + x = 2n − 7
1 2 3 4 21. Si la ecuación:
Indicar el valor de "n". 2n-5 2 n-1 2
4x + (n - 2)x + nx + n - 8 = 0
13. Resolver: tiene 5 raíces. Hallar el producto de las
raíces.
x 4 − x 3 − 7x 2 + x + 6 = 0
Si sus raíces son: x < x < x < x 22. Si ‘‘a’’ es una raíz de la ecuación:
1 2 3 4
Indicar: x + x − (x + x ) 4
1 2 3 4 x - x - 4 = 0. Hallar:
4
4a
3 2 F=
14. Si la ecuación: 2 x − 3x − x + 1 = 0 a+4
tiene una raíz racional. Indique la suma
de sus raíces irracionales.
23. Si las raíces de la ecuación:
3 2
15. Sean las raíces de la ecuación: x - 8x + 7x + k = 0
son proporcionales a 1, 2 y 5.
8 x 4 − 16 x 3 − 3x 2 + x − 24 = 0 Calcular ‘‘k’’.
"x ", "x ", "x ", "x ".
1 2 3 4
Calcular: 2
24. Si la ecuación: 3x - 3x - 1 = 0
M = x1 x 2 x 3 x 4 − (x1 + x 2 + x 3 + x 4 ) Tiene por raíces "x " ∧ " x ".
1 2
Calcular:
16. Se tiene la ecuación: 1 1
x 2n +1 − nx n − 2 x 3 + x 2 − x + (n − 3) = 0 H = 3x1 − + 3x 2 −
x1 x2
que presenta 9 raíces. Calcular el
producto de sus raíces.
25. Sabiendo que la ecuación:
3 2
17. Si: ‘‘x ’’ es una de las raíces de: x - abx + qx + 27 = 0
0
4 tiene sus raíces proporcionales a −1, 3, 9.
3x - 7 = 9x. Calcular:
Calcular ‘‘a . b’’.
4 + 9x 0
H= 4 26. Si: "x " y "x " son raíces de:
x0 − 1 1 2
4 3 2 2x(x - 3) = (x + 3)(x - 1)
18. En la ecuación: x + x + 6 = x + 7x 5 5 3 3 4 4
Indicar sus raíces. x1 + x 2 + 3(x1 + x 2 ) − 8(x1 + x 2 )
Calcular:
19. Calcular la suma de los cuadrados de 27. Calcular la suma de las doce raíces que
las raíces irracionales de la ecuación: presenta la ecuación polinomial:
x 3 − 4x 2 − 2x + 5 = 0 3x
4n+4
- (n + 1)x
4n-2 7
+ nx - (n + 1)x + 8 = 0
20. Sabiendo que "x " es una de las raíces 3 2 2
0 28. Dada la ecuación: ax - a x + ax - 4 = 0
3 2 a∈lN. Si una raíz es ‘‘a’’. Halle el
de: 4x - 8x = 9
Calcular: producto de las otras 2 raíces.

75. Inecuacaciones de Grado Superior Cuarto Año
Tema nº 0 6: i n e c u a c i o n e S D e g r a D o S u p e r i o r
Capacidades:
 Resuelve inecuaciones de grado superior , aplicando criterios adecuados.
Resolver las siguientes inecuaciones:
2 x − 15 5 2
a) > ( 2 − x) > ( 8 − 5x)
2 3 3
2 x − 1 3x − 2 2 x + 1 2
b) + > +
5 6 2 3
3x + 8
c) ≥ −2
x −1
2x − 3 x +1
d) − ( x − 1) ≥
5 4
Resolver las siguientes inecuaciones lineales:
a<x<b ⇒ a<x ∩ x<b
a) El intervalo para el cual se verifica la desigualdad :
3x − 1
3< < 5 ; es :
x−5
b) El número entero “x” que cumple con la desigualdad :
x 12 x + 1
< < ; es :
x + 1 19 x + 2
c) Al resolver la inecuación :
x+4 3
−1 > y sumar los valores enteros que la satisfacen, se obtiene :
x−5 2
Desarrollo del Tema:
1. INECUACIONES LINEALES O DE PRIMER GRADO : Es de la forma :
ax + b > 0 ó ax + b < 0
La solución de esta inecuación es análoga a la solución de una ecuación lineal.
Ejemplo : 5x – 3 < 2x –1 < x + 7
NOTA :
Luego:
5x – 3 < 2x – 1 ∩ 2x – 1 < x + 7
x < 2/3 ∩ x<8
x ∈< -∞, 2/3 >
2. RESOLUCIÓN Y DISCUSIÓN :
Sea la inecuación : ax + b > 0 .......... (1)

76. ax > -b
Si a > 0, dividiendo ambos miembros entre una cantidad positiva el sentido de la
desigualdad no varía.
b
x>−
a
Si a < 0, dividiendo ambos miembros entre una cantidad negativa, el sentido de la
desigualdad se invierte.
b
x<−
a
Si a = 0, la inecuación (1) se reduce a : b > 0
Ella se verifica para todo valor de “x” si b es positivo y se denomina inecuación
indeterminada. Si b es negativo o nulo, carece de raíces y se denomina inecuación
imposible.
Se ha visto que la resolución de una inecuación de primer grado con una incógnita da
lugar a soluciones elementales de la forma :
x>a
Si x > a, se dice que el número “a” es el límite inferior de los valores de la incógnita, lo que
significa que cualquier número mayor que “a” es una solución de la inecuación. La inecuación
x > a se ilustra gráficamente del siguiente modo : sobre el eje numérico se marca el punto
correspondiente al número “a”, los valores de la incógnita “x” que verifican la inecuación, se
representan por los puntos que se encuentran a la derecha del punto “a”.
x>a ó a<x
Como el valor “x” no toma el valor infinito, éste representa el límite superior. La solución se
designa en forma genérica como :
a<x<∞
y aplicando la notación de intervalos como :
x ∈ <a, +∞>
que se lee : “x” pertenece (∈) al intervalo abierto a, +∞
x<b
Si x < b, se dice que el número “b” es el límite superior de la incógnita, lo que significa que
cualquier número menor que “b” es una solución de la inecuación. La inecuación x < b se
ilustra gráficamente del siguiente modo : sobre el eje numérico se marca el punto
correspondiente al número “b”, los valores de la incógnita “x” que verifican la inecuación, se
representan por los puntos que se encuentran a la izquierda del punto “b”. En este caso, el
límite inferior es el valor de menos infinito.
x<b
La solución se designa como :
-∞ < x < b ó x ∈< -∞, b > -∞ b +∞
0
prÁcTica DirigiDa
En cada uno de los ejercicios dados, aplica x
la información teórica recibida. d) 66 < + 2 < 98
4
x
1. Hale el conjunto solución de cada una e) 21 < − 3 < 33
de las inecuaciones :
2
a) 120 < 21x – 6 < 204 f) 4(3x - 1) < 4(x + 9)
b) 5(x + 3) + 4 < x – 1
c) 3x – 14 ≤ 7x – 2 2. Hallar los valores de “x” que satisfacen
a la limitación siguiente :
2x – 5 < x + 3 < 3x – 7

77. Inecuacaciones de Grado Superior Cuarto Año
a) < 5, 8 > b) < 5, 10 > c) < 1, 7 > 2 x − 15 5 2
d) < -4, 8 > e) < 3, 5 > > ( 2 − x) > ( 8 − 5x)
2 3 3
a) 2 b) 4 c) 3 d) 5
3. El intervalo para el cual se verifica la e) 6
3x − 1
desigualdad : 3 < < 5 ; es :
x−5 11. Resolver :
a) 5 < x < ∞ b) 3 < x < 5 1
c) -∞ < x < 5 d) 12 < x (x – 1)*2 ≤ (3*x)* ≤ (1+2x)*5, si en R
2
< ∞ e) 15 < x < ∞
a−b
definimos la operación a*b =
4. El número entero “x” que cumple con la 2
x 12 x + 1 7 8 6 8
desigualdad : < < ; es : a)  ,  b)  ,  c) <
x + 1 19 x + 2  3 3  3 3
a) 1 b) 2 c) 3 d) 4 e) 5 7 8
, ]
5. La solución de la inecuación : 3 3
3 7 
>1 ; es : d)  ,8 e) N.A.
x−4 3 
a) 1<x<4
b) 4<x<7 12. La suma de los valores enteros y
c) -∞ < x < 1 ; 4 < x < ∞ positivos de “x” que satisfacen a la
d) -∞ < x < 4 ; 7 < x < ∞ siguiente inecuación :
e) 4<x<5;7<x<∞ 5 x +13 8 x +1
5 7 ; es :
3 2
> 27 4
6. Al resolver la inecuación : a) 1 b) 2 c) 3 d) 6
x+4 3 e) 10
−1 >
x−5 2
y sumar los valores enteros que la 13. El triple de un número es mayor que 14
satisfacen, se obtiene : y menor que 16. ¿Cuál es el número?.
a) 40 b) 44 c) 45 d) 50 e) 56 a) 5 b) 7 c) 9 d) 11
e) 15
7. ¿Cuáles son los números naturales que
al multiplicarlo por 6, siempre da un 14. Resolver :
6x − 3 x−3
número menor que 36?
− ( 2 x − 6) ≥
2 4
8. Jorge fabrica un número determinado a) [ -7, +∞> b) [ -7, 8> c) [ -7, 0]
de mesas. Si duplica su producción y d) [7, 25] e) [7, +∞ >
vende 60, le quedan más de 24. Luego
fabrica 10 más y vende 28. Tendrá 15. Resolver :
entonces menos de 10 mesas. ¿Cuántas 3x + 8
mesas se fabricaron? ≥ −2
a) 96 b) 43 c) 45 d) 88 e) 120 x −1
a) < -∞, -6/5 ] ∪ < 1, +∞ >
9. El intervalo en el cual debe estar b) < -∞, 5/6 ] ∪ < 2, +∞ >
comprendido el número “n” para que la c) < -∞, -1 ] ∪ < 2, +∞ >
raiz de la ecuación : d) < -∞, -1 ] ∪ [ 1, +∞ >
3 2n − 1 e) < -∞, 6 ] ∪ [ 7, +∞ >
= sea menor que 1 , debe ser :
x x+n
a) –2 < n < 4 16. Resolver :
b) –4 < n < 2 1 x−3 2
c) -∞ < n < -4 ; 2 < n < ∞
< <
5 x +1 3
d) -∞ < n < -2 ; 4 < n < ∞ a) < 4, 11 > b) [ 4, 11 ] c) < 4,
e) -∞ < n < 2 ; 4 < n < ∞ 12 ] d) < 0, 7 > e) N.A.
10. ¿Cuántos números enteros, satisfacen la 17. Resolver :
inecuación?

78. 6 5 d) < -∞, -2> ∪ < 0, 1 >
− > −2 e) N.A.
x −1 x − 2
a) < -∞, -1/2 > ∪ < 1, 2> ∪ < 3, +∞>
20. Resolver :
b) < -∞, -1 > ∪ < 5, 6> ∪ < 6, +∞>
c) < -∞, -2 > ∪ < -1, 2> ∪ < 3, +∞>
2x + 1 − x − 8 > 3
d) < -∞, -1/2 > ∪ < 3, +∞> a) [ 8, 12 > ∪ < 24, ∞ >
e) < -∞, -1/2 ] ∪ < 1, 2> ∪ [ 3, +∞> b) [ 3, 15 > ∪ < 15, ∞ >
c) [ 0, 9 ] ∪ < 10, 18 ]
18. En R definimos la operación * por : d) [ 8, 12 ] ∪ [ 24, ∞ >
a+b e) N.A.
a*b = ; según esto, resolver :
2 21. En un gallinero había un cierto número
( 2 x − 1) *1 ≤ ( 2 * x ) * 3 ≤ ( 3 + 2 x ) * 5 de gallinas. Se triplico este número y se
vendieron 95, quedando menos de 87.
4
a) [ 5/6, +∞ > b) [ 7/9, +∞ > Después se duplicó el número de
c) [3, 19] d) [ 6/7, +∞ > gallinas que había al principio y se
e) N.A. vendieron 40, quedando mas de 79.
¿Cuántas gallinas había inicialmente en
19. Resolver : el gallinero?
a) 20 b) 30 c) 40 d) 60
x +3
( 0.04) 2 x −1 > x ( 0 .2 )
2 x −1
e) 80
a) < -∞, -3 > ∪ < 0, 1/2 > 22. Investiga y resuelve las existencias de
b) < -∞, 0 > ∪ < 0, 1 > ejercicios de diversas complejidades que
c) < -∞, 5 > ∪ < 1, 5/6 > pudieran existir con inecuaciones
lineales o de primer grado.
INECUACIONES DE SEGUNDO GRADO
EXPLORACIÓN Y MOTIVACIÓN
Estimado alumno, exploremos nuestros saberes previos:
a) Resolver : 3 x 2 − 10 x + 3 < 0
b) Resolver : x 2 + 6 x + 15 > 0
c) Resolver : (x 2
+ 2 x − 3)( 3 x − 4 − x 2 ) > 0
x2 + x + 2
d) Resolver : 3 ≤0
x − x 2 − 2x
e) Resolver : ( x − 2 − x )( x2 2
+ 2 x − 8) < 0
f) Resolver : x 2 − 4 x + 6 < 0
g) Resolver : x 2 + 6 x + 15 > 0
1 1
h) Resolver la siguientes inecuación : > 2
x − 2 x − 15 x − x − 2
2
3. INECUACIONES DE SEGUNDO GRADO CON UNA INCÓGNITA : Una inecuación de
segundo grado con una incógnita es aquella que puede reducirse a la forma :
ax 2 + bx + c > 0 ó

79. Inecuacaciones de Grado Superior Cuarto Año
ax 2 + bx + c < 0
Siendo a ≠ 0 y positivo, si “a” fuera negativo se multiplican ambos miembros por –1 para
hacerlo positivo, con lo cual se cambia de sentido a la desigualdad.
Resolver una de estas inecuaciones es hallar entre que intervalos debe variar “x” para que
satisfaga a la condición impuesta.
4. RESOLUCIÓN : Para determinar las soluciones de una inecuación de segundo grado se
aplica cualquiera de estos dos procesos :
1. Se factoriza el trinomio ax 2 + bx + c , si no fuera factorizable directamente se
encuentran las raíces x’ y x’’ de la ecuación :
ax 2 + bx + c = 0 , con lo cual se tendrá :
( x − x')( x − x' ') > 0 ó
( x − x')( x − x' ') < 0
Es decir, la inecuación dada se reduce a dos inecuaciones lineales que permiten resolver
el problema.
2. Aplicando las propiedades del trinomio ax 2 + bx + c y la representación gráfica, dan las
soluciones con gran sencillez.
prÁcTica DirigiDa
1. Resolver la inecuación : x 2 − 8 x + 12 > 0 e) N.A.
a) 6 < x < +∞ ∪ -∞ < x < 2 X −1 X +2
6. Si: ≥ Hallar la
b) 2 < x < +∞ ∪ -∞ < x < 0 ( X + 1)( X + 2) ( X + 1)( X − 1)
c) 1 < x < +∞ ∪ -∞ < x < 1 suma del valor entero máximo y mínimo
d) 6 ≤ x < +∞ ∪ -∞ < x ≤ 2 del conjunto solución.
a)-1 b)2 c)0 d)4 e) –5
2. Resolver : x 2 + 2 x − 35 < 0
a) x ∈ < -7, 5 > 7. Hallar el mayor valor de “m” que
b) x ∈ < -2, 7 > cumple la relación: 33 + 14 x + x 2 ≥ M
c) x ∈ < 0, 7 >
d) x ∈ < -2, 5 >
∀x ∈ ℜ
e) N.A. a)-16 b)-11 c)-12 d)-13 e)-14
8. Hallar el menor valor entero del
3. Resolver : x 2 − 10 x + 25 > 0 conjunto solución en:
a) x ∈ R – {5} b) x ∈ R
2
c) Absurdo d) x = 5 x − 2x + 3
e) x ∈ < -5, 5> ≤ −3 .
2
x − 4x + 3
4. ¿Qué valores de “x” verifican la a)2 b)3 c)-1 d)0 e) –3
3x + 2 4x − 7
desigualdad? +2< 2
x−5 x−5 x 2a 8a
a) x ∈ < 4, 7 > b) x ∈ < 1, 5 > 9. Resolver: − ≤
2 2
; si a<0
x−a x+a x −a
c) x ∈ < 0, 2 > d) x ∈ < -1, 7 >
e) N.A. [
a) − 3a , − a > U < a , 2a > b) < -3a, -a >
c) < a,2a > d)< 3a, 5a>
5. Resolver : 4 x 2 − x − 5 > 0 e) [-a, 3a >
a) x∈R
10. Resolver :
b) x ∈ < - ∞, -1/4> ∪ < 5, +∞ >
x
c) x ∈ < - ∞, -5> ∪ < 0, +∞ > x2 − ≤ 6
d) x ∈ < - ∞, -3/5> ∪ < 1, +∞ > 3+ 2

80. a) < 2, 3 > b) < − 2 ,− 3 > a) 12 b) 13 c) 14 d) 15
[ ]
e) 16
c) < − 2 , 3 > d) − 2, 3
e) < −∞,− 2 ]∪[ 3 ,+∞ ] 14. Hallar el mayor número real “m” tal
que se cumpla :
11. Resolver :
m ≤ x 2 − 4 x + 41 ; para todo “x” real.
(x 2
+ 2 x − 3)( 3 x − 4 − x 2 ) > 0
a) 37 b) 38 c) 39 d) 40 e) 41
a) x ε <-3, 1> b) x ε <-3, 1] 15. Resolver : 2 x + 1 − x − 8 > 3
c) x ε <-1, 3> d) x ε [-3, 1]
e) N.A. a) x ∈ [ 8, 12 > ∪ < 24, +∞ >
b) x ∈ < - ∞, -1> ∪ < 0, +∞ >
12. La solución de la inecuación : c) x ∈ < 9, 18 ] ∪ [ 5, +∞ >
d) x ∈ < - ∞, 0> ∪ < 24, +∞ >
x2 + x − 6 e) x ∈ < - ∞, -1/2> ∪ < 5, +∞ >
<0
x 2 + 13 x + 30
–10 < x < 2 16. Resolver : 2 x − 5 > x 2 − 2 x + 10
f) –10 < x < -3; -3 < x < 2
a) x ∈< 5, +∞ > b) x ∈[ 5, +∞ >
g) -∞ < x < -2; 3<x<5 c) x ∈< 2, +∞ > d) x ∈< 5/2, +∞ >
h) –3 < x < 2 e) x ∈< -∞, 5/2 > ∪ [5, +∞ >
i) -∞ < x < -3; -3 < x < ∞
17. Investiga y resuelve las existencias de
13. Hallar el menor número real M tal que ejercicios de diversas complejidades que
se cumpla : 6 + 6 x − x 2 ≤ M ; para todo pudieran existir en un sistema de
“x” real inecuaciones cuadráticas o de segundo
grado.
inecuacioneS De graDo Superior
a) Resolver : x 3 − 2 x 2 − 8 x > 0
b) Resolver : x 4 − 4 x 3 − 15 x 2 + 19 x + 30 < 0
x2 + x + 2
c) Resolver : 3 ≤0
x − x 2 − 2x
2 x − 74
d) Resolver: x 2 + 3x + 8 ≤
x−7
Resolver las siguientes inecuaciones :
a) Resolver :
x 4 − 2 x 3 − 5 x 2 − 11x − 1
> −1
x2 + x + 4
b) Resolver :
4( x − 1) < ( x + 5)(3 x + 4)
c) Resolver :
x 2 − 5x + 6
≥0
x 2 + x − 42
d) Resolver la siguientes inecuación :
− x 3 + x 2 + 22 x − 40
≥0
x ( x + 7)

81. Inecuacaciones de Grado Superior Cuarto Año
5. INECUACIONES DE GRADO SUPERIOR : Una inecuación de grado superior a dos con
una incógnita es aquella que se puede reducir a la forma :
a 0 x n + a1 x n −1 + a 2 x n − 2 + ... + a n > 0
ó
a 0 x n + a1 x n −1 + a 2 x n − 2 + ... + a n < 0
Donde n ≥ 3 y a0 ; si a0 no fuera positivo se hace positivo.
6. RESOLUCIÓN : Para determinar las
soluciones de una inecuación de grado superior con una incógnita, se encuentran las “n”
raíces :
x1 < x2 < ... < xn de :
a 0 x n + a1 x n −1 + a 2 x n − 2 + ... + a n = 0
Con lo cual se obtiene :
(x – x1)(x – x2) ... (x - xn) > 0
ó
(x – x1)(x – x2) ... (x - xn) < 0
Donde el producto del primer miembro tiene sus factores ordenados de mayor a menor.
7. MÉTODO ANALÍTICO :
a) Si las raíces son reales y desiguales, se encuentran los intervalos formados por estas
raíces y los valores extremos +∞ y -∞ ; colocando signos alternadamente (+) y (-),
viniendo de derecha a izquierda, en los intervalos consecutivos del producto.
b) Para la solución se toman los intervalos que tienen signo igual al sentido de la
desigualdad.
c) Si hay raíces dobles, los trinomios que
- + _- +
dan origen a estas raíces iguales se
pueden dejar de escribir en la
-∞ x1 xn +∞ inecuación, teniendo cuidado de no
x2
tomar en la solución los puntos para
los cuales existe la raíz doble.
d) Si hay raíces complejas (estas se presentan por pares conjugados) los trinomios que
dan origen a estas raíces complejas conjugadas son siempre positivas, por lo cual se
pueden dejar de escribir en la inecuación.

82. prÁcTica DirigiDa
En cada uno de los ejercicios dados, aplica la información teórica recibida
1. Resolver la inecuación : c) < -∞, -1 > ∪ < 2, +∞ >
x 3 − 9 x 2 + 26 x − 24 < 0 d) x ∈ R –{-1}
a) x ∈ < - ∞, -1/4> ∪ < 5, +∞ > e) < -7, -1 > ∪ [ 3, 4 >
b) x ∈ < - ∞, 2> ∪ < 3, 4 >
c) x ∈ < - ∞, -1> ∪ < 8, +∞ > 7. Resolver :
d) x ∈ < - ∞, -2> ∪ < 5, +∞ > x 5 − 2 x 4 − x 3 − 2 x 2 − 20 x + 24 < 0
e) N.A.
a) < -∞, -2 > ∪ < 2, +∞ >
2. Resolver : b) < -∞, -1 > ∪ < 0, +∞ >
c) < -∞, -2 > ∪ < 1, 3 >
( x − 2)( x − 4) 2 <0 d) < -∞, 0 > ∪ < 1, 3>
( x + 3)( x − 7 ) e) N.A.
x∈< -∞, -3 > ∪ < 2, 7 > -{4}
x∈< -∞, 0 > ∪ < 3, 5 > -{4} 8. Resolver :
x∈< -∞, -3 > ∪ < 0, 7 > -{4} 2
x − x − 12
x∈< -∞, -3 > ∪ < 2, +∞ > -{4} <0
N.A. 2
x − 2x + 3
a) x ∈ < -3, 4 > b) x ∈ < -3, 0 >
3. Resolver : c) x ∈ < -3, +∞ > d) x ∈ < -3, 7 >
( x − 1)( x − 3) ≥ 0 e) x ∈ < -3, 4 > ∪ < 7, +∞ >
( x − 4 ) 2 ( x + 5) 9. Resolver :
a) x ∈ <-5, -3> ∪ [ 3, 4 > ∪ < 4, +∞
2x 4 + 3x 3 − 6x 2 − 5x + 6
> <0
b) x ∈ < -∞, -3 > ∪ < 2, +∞ > x 3 − 7 x 2 + 18x − 40
c) x ∈ < -∞, -3 > ∪ < 2, 7 > -{4}
d) x ∈ < -5, 1 ] ∪ [ 3, 4 > ∪ < 4, +∞ a) < -∞, -2 ] ∪ [ -3/2, 5>
> b) < -∞, -2 > ∪ < -3/2, 5>
e) N.A. c) < -∞, 0 ] ∪ [ 1, 5>
d) < -∞, -2 ] ∪ [ 2, +∞ >
4. ¿Qué valores de “x” verifican la e) N.A.
desigualdad?
x +1 10. Resolver :
<0
x + 8 x 2 + 14 x + 12
3 (x 2
+ 2 x − 3)( 3 x − 4 − x 2 ) > 0
a) <-10, 0> b) <-6, 0 > c) a) x ε <-3, 1> b) x ε <-3, 1] c) x ε
<-6, -1> <-1, 3> d) x ε [-3, 1] e)
d) <-2, 5 > e) N.A. N.A.
5. Resolver : 11. Resolver :
x 4 + 2x3 − 9x 2 − 2x + 8 > 0 x 2 − 2 x − 15 > x + 1
a) < -∞, -4 > ∪ < -1, 1 > ∪ < 2, +∞ > a) < -∞, -1] ∪ [ 3, +∞ >
b) < -∞, -6 > ∪ < 0, +∞ > b) < -∞, -1> ∪ < 3, +∞ >
c) < -∞, -1 > ∪ < -1, 0 > ∪ < 1, +∞ > c) < -∞, -3]
d) < -4, 2> d) < -∞, 0] ∪ [ 1, +∞ >
e) < -∞, -1 > ∪ < 0, 1 > ∪ < 3, +∞ > e) N.A.
6. Resolver : 12. Resolver :
2 x 4 − 7 x 3 − 11x 2 + 22 x + 24 < 0
a) < -3/2, -1 > ∪ < 2, 4 >
x +1
8 x +3 < x −1 32 2 x +3
b) < -3/2, 0 > ∪ < 1, 4 > Rpta. : < -∞, -1> ∪ < 1, +∞ >

83. Inecuacaciones de Grado Superior Cuarto Año
pudieran existir en un sistema de
13. Investiga y resuelve las existencias de inecuaciones grado superior.
ejercicios de diversas complejidades que

84. Tema nº 0 7: i n e c u a c i o n e S c o n v a l o r a b S o l u T o
Capacidade
s:
 Resuelve inecuaciones con valor absoluto, aplicando criterios vistos en clase.
Desarrollo del Tema:
Teoremas  1 
a ∈ IR  − 4 ; 3
 |x| > a ↔ x > a ∨ x < -a ∴ C.S. =  
 |x| < a ↔ a > 0 ∧ -a < x < a 3. Resolver:
2 2
|x + x - 2| < |x | + |x - 2|
 |x| = |y| ↔ (x + y)(x - y) = 0 Resolución: |a + b| < |a| + |b|
∴∀ x; y ∈ IR; |x + y| ≤ |x| + |y| sólo si: ab < 0
(Desigualdad triangular) Dando forma a la inecuación propuesta:
Nota: 2 2
|(x ) + (x - 2)| < |x | + |x - 2|
|x + y| = |x| + |y| ↔ xy ≥ 0 del teorema se tiene:
|x + y| < |x| + |y| ↔ xy < 0 2
x (x - 2) < 0
2 x-2<0↔x≠0
1. Resolver: x ≥ 3|x| + 4 x<2
Resolución: x ∈ <-∞; 2> - {0}
2 2
Se sabe que: x = |x| . Luego se tendrá: le restamos el cero, pues: x = 0, no verifica la
2 inecuación original.
|x| ≥ 3|x| + 4
2
|x| - 3|x| - 4 ≥ 0
4. Resolver: |x + 1| < |x - 2|
(|x| - 4)(|x| + 1) ≥ 0
Resolución:
Observa que: |x| + 1 > 0; ∴∀ x ∈ IR
Elevando al cuadrado:
En consecuencia: |x| - 4 ≥ 0 ↔ |x| ≥ 4 2 2 2 2
x ≥ 4 ∨ x ≤ -4 |x + 1| < |x - 2| ↔ (x + 1) < (x - 2)
2 2
∴ x ∈ <-∞; -4] ∪ [4; +∞> (x + 1) - (x - 2) < 0
Diferencia de cuadrados:
2. Resolver: |5x - 2| ≤ 3x + 4 [x + 1 + x - 2][x + 1 - x + 2] < 0
Resolución: (3)(2x - 1) < 0
4 6x - 3 < 0 → 6x < 3
I. 3x + 4 ≥ 0 ↔ x ≥ - ... S
3 1 1
1 - ∞;
II. |5x - 2| ≤ 3x + 4 2
→ -(3x + 4) ≤ 5x - 2 ≤ 3x + 4 x< 2 ∴x∈
→ -2 ≤ 8x ∧ 2x ≤ 6
1 5. Resolver:
→- ≤x∧x≤3 2
(x - 2) > 4|2 - x| + 5
4 Resolución:
 1  Por propiedades:
- 4 ; 3 2 2
→ x ∈  ... S (x - 2) = |x - 2|
2
|2 - x| = |-2 + x| = |x - 2|
III. x ∈ S ∩ S
1 2 Reemplazando:
Graficando: 2
|x - 2| - 4|x - 2| - 5 > 0
−∞ +∞ (|x - 2| - 5)(|x - 2| + 1) > 0
Pero: |x - 2| + 1 > 0 ∴∀ x ∈ IR
4 1 ∴ |x - 2| - 5 > 0
- - 3
3 4 |x - 2| > 5
x - 2 > 5 ∨ x - 2 < -5
x > 7 ∨ x < -3
Graficando:

85. Inecuaciones con Valor Absoluto Cuarto Año
x ∈ <-∞; -3> ∪ <7; +∞>
-∞ -3 7 +∞

86. problemaS propueSToS
2
1. Resolver: |x - 3x - 1| < 3
a) <-∞; 1> ∪ <1; 2> b) <-1; 1> ∪ <2; 4> 10.Sabiendo que: b > 0 ∧ |x - a| < 2b
c) <-1; 1] ∪ <2; 4] d) <0; 1> ∪ <2; 4> Hallar la variación de:
e) <-1; 1> ∪ <4; +∞> b
x - a + 3b
2 1 1 1
2. Resolver: |x - 2x - 4| ≥ 4 ;1 - 1; ;1
a) 3 b) 5 c) 5
a) <-∞; -2] ∪ [4; +∞>
b) <-∞; -2] ∪ <0; 2] 3 1 1
1; - ;
c) <-∞; -2] ∪ <0; 2] ∪ [4; +∞> d) 2 e) 5 5
d) <-∞; -2] ∪ [0; 2] ∪ [4; +∞>
e) <-∞; -2] ∪ [2; 4] 6. Si: |x - 3| < 5; halle el intervalo en el que se
encuentra la siguiente expresión:
2 2
3. Resolver: (x - 5) - 10 ≤ 3|5 - x| F(x) = |(x - 2) - 5|
a) [0; 10] b) <0; 10> a) [-5; 31] b) [0; 31> c) [0; 36>
c) IR - {0; 10} d) φ d) <0; 36] e) [-5; 32>
e) <-∞; 0> ∪ <10; +∞>
2 2
7. Resolver: |x - x - 3| < |x + 2|
2
4. Resolver: (x - 2) - 15 > 2|2 - x| 1 1
- ∞; - ∞; -
a) IR - [-2; 6] b) IR - [-2; 7] a) 2 ∪ <1; 5> b) 2 ∪ <1; 5>
c) IR - [-1; 7] d) IR - [-3; 7] 1 1
e) IR - [-3; 6] - ;1 - 5; -
c) 2 ∪ <5; +∞> d) 2 ∪ <1; +∞>
5. Resolver: e) <-∞; -5> ∪ <1; +∞>
2
(|x - 1| + |x - 2|)(|1 - x| - |2 - x|) ≤ x - 6
8. Si: |x - 1| < 1, Halle el menor valor entero de |
a) x ∈ IR b) x ∈ φ 2
c) x ∈ IR - {2} d) x∈<-∞; -1] ∪ [3; +∞> F|, además: F(x) = x - 4x + 7
e) x ∈ [-1; 3] a) 8 b) 4 c) 5
d) 6 e) 7
2 2 2
6. Resolver: |x - 2| ≤ 3|x - 2| + 4 2 2
9. Resolver: |x + x - 1| ≤ |x - x + 3|
a) [- 2 ; 2 ] b) [0;
6 ] a) [2; +∞> b) <-∞; 2]
c) <-∞; 2> d) <-∞; 1> ∪ [2; +∞>
c) [-
3 ;
3 ] d) [-
6 ;
6 ] e) N.A.
e) [0;
3 ] 10.Halle el conjunto "A" por extensión si:
3 2
A = {x ∈ IR / |x - 1| ≤ |x + x + 1|}
7. Resolver: ||x| + 2| ≤ |x|
2 a) [1; 2] b) [0; 2] c) <2; 3>
a) <-∞; -2] ∪ [2; +∞> b) [-2; 2] 2
c) [0; 2] d) [-2; 0] d) [0; 4] e) [0; ]
e) [1; 2]
16. Si: |x| < 3. Hallar el mínimo valor de "P".
2
8. Resolver:
2
|x - 4| ≤ (x + 2)
2 Con P(x) = (x +2) + 5.
a) x ∈ [0; 2] ∪ {-2} b) x ∈ [0; 6] - {2}
2
c) x ∈ IR
+
- {-2} d) x ∈ IR
+
∪ {-2} 17. Resolver: |x - x + 1| ≤ 1. Luego indicar un
0 0 elemento del conjunto solución.
e) x ∈ IR
2 2
2 2
19. Resolver: 2x + 11 ≤ x + |7x| - 1
9. Resolver: |x - 3| < |x - x + 2|
1 1 2
- ∞; -∞ ; - 20. Resolver: x - 8x + 10 + |x - 4| ≤ 0
a) 2 ∪ <1; 5> b) 2 ∪ <1; 5>
1
- ∞; 21. Resolver: ||x| - 3| ≥ ||x| - 1|
c) <-∞; -2> ∪ <1; 5> d) 4 ∪ <1; 5>
e) <-∞; 1> ∪ <1; 5> 2 2
22. Resolver: |x + 3x - 10| ≤ | x + x - 6|

87. Inecuaciones con Valor Absoluto Cuarto Año
2 2
23. Resolver: |x - 2| > 3|x -2|+ 4 x x 7
24. Si: |x - 2| < 4. Halle el intervalo en el que se
encuentra la siguiente expresión: H(x) = 2 2 ≤ 4
28. Resolver: +3
| ( x − 6 ) + 36 |
2
29. Dados los conjuntos:
2
25. Resolver: |x -1| - x + 1 > 0 A = {x ∈ IR / |x - 2| < |x +1| }
B = {x ∈ IR / |x - 4| + |x - 2|< |x +3| }
26. Resolver: |5x - 4| ≤ |3x + 2| + 2 |x -3| Hallar: A ∩ B.
27. ¿Cuál será el conjunto de números enteros no 30. Si: a > 0 ∧ b < 0
negativos que cumplan la desigualdad? Además al resolver:
|x - 1| + |x| ≤ 1 - 2x 2
|bx - 3b| + |3a - ax| < a - b
2
Se obtiene como C.S.: <p; q>
Hallar: p + q.

88. T ema nº 08: SiSTema De inecuacioneS
Capacidade
s:
 Resuelve problemas sobre sistema de inecuaciones.
Desarrollo del Tema:
SISTEMA DE INECUACIONES
a) Graficar y dar las soluciones comunes del sistema :
x > 5 ............... (1)
x > -3 ............... (2)
b) Dar las soluciones comunes del sistema :
x > -2 ........... (1)
x < 3 ........... (2)
c) Resolver el siguiente sistema :
( x – 1 )( x + 2 ) > ( x + 4 )( x – 2 ) ... (1)
( x + 3 )( x + 1 ) > ( x + 4 )( x – 3 ) ... (2)
d) La suma de los valores enteros de “x”
que satisfacen al siguiente sistema :
5x – 1 > 0 ............ (1)
3x – 11 < 0 ............ (2)
7x – 23 < 0 ............ (3)
24x – 5 > 0 ............ (4)
Resolver el siguiente sistema de inecuaciones:
a) En el sistema de inecuaciones :
2x + 5y < x – 4 ................ (1)
3x – 2 > 4x – 8 – 2y ................ (2)
El número de valores enteros, positivos y diferentes de “x” que dan valores enteros para
“y”, es:
b) El valor entero y positivo de “x” que satisface al siguiente sistema :
3
x −3 y =1 .......... (1)
127 < x − y < 217 .......... (2)
c) Entre Jaime y Carlos tienen menos de 6 hijos, Carlos tiene mas hijos que Eusebio, y
aunque Jaime tuviera un hijo menos, seguiría teniendo más hijos que Eusebio. ¿Cuántos
hijos tiene cada uno de ellos?
d) Se sabe que el cuádruplo del número de monedas que hay dentro de una bolsa es tal, que
disminuido en 5, no puede exceder de 31, y que el quíntuplo del mismo número de
monedas aumentado en 8, no es menor que 52. ¿Cuál será dicho número?
BÁSICO CONCEPTUAL:
8. SISTEMA DE INECUACIONES : Se llama sistema de inecuaciones, al conjunto de
inecuaciones que se verifican para los mismos valores numéricos de las incógnitas.
Así las inecuaciones :
ax + b > 0 ............ (1)

89. Sistema de Inecuaciones Cuarto Año
cx + d > 0 ............ (2)
ex + f > 0 ............ (3)
Forman un sistema de tres inecuaciones de primer grado con una incógnita.
Resolver dicho sistema, es determinar los límites entre los cuales están comprendidas las
soluciones comunes a todas las inecuaciones.
Si las inecuaciones no admiten ninguna solución común, se dice que el sistema es
incompatible, imposible o absurdo.
Si en el sistema hay alguna inecuación incondicional, podrá suprimirse, pero si hubiese
alguna imposible, el sistema sería incompatible.
9. RESOLUCIÓN : Para determinar las soluciones de un sistema de primer grado con una
incógnita, se debe de tener en cuenta lo siguiente :
3. Se hallan las soluciones de cada inecuación por separado.
4. Se comparan para establecer las soluciones comunes a todas las inecuaciones.
La elección de las soluciones comunes se facilita si las soluciones de cada inecuación se
representan sobre el eje numérico.
prÁcTica DirigiDa
En cada uno de los ejercicios dados, aplica c) x = 1 ; y = 3 d) x = 10 ; y = 1
la información teórica recibida e) x = 2 ; y = 7
1. Dar las soluciones comunes del sistema
5. La suma de los valores enteros de “x”
x < -1 ............ (1)
que satisfacen al siguiente sistema de
x < 4 ............ (2)
inecuaciones :
a) -∞ < x < -1 b) -∞ < x < 0
c) -∞ < x < 2 d) –1 < x < +∞ 13 x − 5 3 x − 8 2 x + 7
+ > + 1 ...... (1)
e) –1 ≤ x < +∞ 2 5 3
3x − 1 x +1 x
2. Dar las soluciones de : −1 < − ...... (2)
x > 2 .............. (1)
5 2 7
a) 5 b) 9 c) 14 d) 20 e) 27
x < -1 .............. (2)
a) < -∞, -1 ] ∪ [ 2, +∞ >
6. Hallar las soluciones enteras y positivas
b) < -∞, 0 > ∪ < 3, +∞ > de “x”, “y”, “z” que satisfacen al siguiente
c) < -∞, -1 > ∪ < 2, +∞ > sistema :
d) < -∞, 0 ] ∪ [ 3, +∞ > 2x + 3y +5z > 23 .......... (1)
e) < -∞, 0 > ∪ < 1, +∞> 2x – y + 5z < 13 .......... (2)
y–z >1 .......... (3)
3. Hallar los valores enteros de “x” e “y” y<4 ......... (4)
en: f) x=1,y=2,z=3
5x – 3y > 2 ................. (1) g) x=5,y=3,z=1
2x + y < 11 .................. (2) h) x=4,y=1,z=1
y > 3 .................. (3) i) x=0,y=2,z=4
a) x = 2 ; y = 4 b) x = 4 ; y = 3 j) N.A.
c) x = 3 ; y = 4 d) x = 4 ; y = 2
e) x = 1 ; y = 3 7. Siendo “x”, “y”, “z” los valores enteros que
satisfacen al siguiente sistema de
4. Hallar las soluciones enteras y positivas inecuaciones :
de “x” é “y” que satisface al siguiente x + y + z > 14 ........... (1)
sistema : x – y + z < 6 ........... (2)
2x – 5y > x + 4 ............ (1) Y < z ........... (3)
3x + 13 > 2y + 4x ............. (2) Z < 7............. (4)
a) x = 7 ; y = 5 b) x = 3 ; y = 9 El valor de la expresión:

90. x
y 3 − z 2 − 8 ; es: 1
c) < x <1 d) 1 < x < 5
a) 1 b) 2 c) 3 d) 4 2
e) 5 1
e) − 2 < x < ; 1< x < 5
2
8. En el sistema de inecuaciones :
2x + 5y < x – 4 ............... (1) 13. La solución del sistema de inecuaciones :
3x – 2 > 4x – 8 –2y ............... (2)
El número de valores enteros, positivos x+2
11x −5 − 1 > 0 .......... (1)
y diferentes de “x” que dan valores
enteros para “y”, es:
x −3
4 x + 5 − 2 x −1 > 0 ......... (2) , es :
a) 1 b) 2 c) 3 d) 4 e) 5 k) 5<x<7
l) 3<x<5
9. El valor entero de “x” que satisface al m) –2 < x < -1
siguiente sistema de inecuaciones : n) -∞ < x < -2 ; 5 < x < 7
x + y > 76 ............. (1)
o) 3 < x < 5 ; 7 < x < +∞
x – y < 10 ............. (2)
x + 2y < 112 ............. (3) ; es :
14. La solución del siguiente sistema de
a) 34 b) 35 c) 42 d) 43 e) 44
inecuaciones :
10. Las soluciones enteras y positivas de “x” 4 x 2 + 3x + 2 > 0 ........... (1)
é “y” que satisfacen al siguiente sistema x 2 + 6 x − 72 < 0 ........... (2)
de inecuaciones : x 2 − 12 x − 45 >0 ............ (3)
y − x 2 − 3 x + 8 > 0 .......... (1) a) -12 < x < -3 b) –3 < x < 6
2 y − x < 4 .......... (2) c) 6 < x < 15 d) -∞ < x < -12
a) x1 = 1 ; y1 = 1 b) x1 = 2 ; y1=1 e) 15 < x < ∞
c) x1 = 1 , y1 = 1 ; x2 = 2 ; y2 = 2
d) x1 = 1 , y1 = 1 ; x2 = 1 ; y2 = 2 15. Entre que límites debe estar
e) x1 = 1 , y1 = 1 ; x2 = 2 ; y2 = 1 comprendido el valor de “K” para que el
x 2 − kx + 1
11. Resolver el siguiente sistema de valor de la fracción : esté
x2 + x +1
inecuaciones:
comprendido entre (-3) y (+3) para
x+2 x−3 todo valor de “x”.
> ................... (1)
x+9 x+3 a) –5 < k < 1 b) –2 < k < 0
x −1 x − 5 c) –1 < k < 6 d) 2 < k < 8
< ................... (2) e) –4 < k < 7
x − 4 x −1
a) –8 < x < 5 ∪ 10 < x < 41
16. Dado : x > 0, y > 0, x > y é z ≠ 0 ,
b) –3 < x < 0 ∪ 1<x<3
la desigualdad que no siempre es
c) –∞ < x < 2 ∪ 2 < x < 33
correcta es:
d) –3 < x < 1 ∪ 21 < x < 33
a) x + z > y + z b) x – z > y – z
e) –3 < x < 1 ∪ 1 < x < 41
x y
c) xz > yz d) 2
> 2
12. La solución del sistema de z z
inecuaciones : e) xz > yz
2 2
x +7 x−8
< ................ (1)
x + 2 x −1 17. Investiga y resuelve las existencias de
x+4 x−3 ejercicios de diversas complejidades que
> ................ (2) ; es : pudieran existir en un sistema de
x−5 x+2 inecuaciones lineales o de primer grado.
3 1 3
a) − < x < b) − 2 < x < −
4 2 4

91. Sistema de Inecuaciones Cuarto Año
Tema nº 9: binomio De newTon
Capacidades:
 Define correctamente el factorial de un número.
 Opera con factoriales.
 Opera con números combinatorias.
 Resuelve problemas sobre binomio de Newton
Desarrollo del Tema:
Introducción: El desarrollo del binomio de Newton se aplica para poder determinar los términos del
resultado de potencias binomios, cuando los exponentes son números naturales mayores que tres, pues
cuando los exponentes son pequeños podemos aplicar productos notables.
Cuando se asignan valores a las variables se pueden generar diversas sumatorias con número
combinatorios, las cuales serian difíciles de sumar sin usar el binomio de Newton, por ejemplo se llega a
20 20 20 20 20 20
calcular que: C 0
+ C1 + C2 + C3 + C4 + ... + C20 = 220 en forma directa, pues 220 es el resultado de
desarrollar; (1 + 1)20 por Binomio de Newton.
CONCEPTOS PREVIOS
FACTORIAL PROPIEDADES:
El factorial de un número sólo está definido en el 1. Si a! = b! ⇒ a = b , ∀ a, b ∈ Z+
conjunto de los número naturales y es igual el Ejemplo: x! = 24 ⇒ x! = 4! ⇒ x = 4
producto del número dado, por todos los número (2x – 1)! = 6 ⇒ (2x – 1)! = 3!
naturales menores que él, sin incluir el cero. → 2x – 1 = 3
2x = 4 ⇒ x = 2
NOTACIÓN 2. Si a! = 1 ⇒a = 1 ∨ a = 0
Para indicar el factorial de un número empleamos
cualesquiera de los siguiente símbolos ! ó L.
3. n! = n (n – 1)! , ∀ n ∈ Z+ ∧ n > 1
n! ∨ n Ejemplo: 6! = 6 . 5 . 4 . 3 . 2 . 1
Se lee: “factorial de n” 5!
Por definición: n =⋅
1 2 ⋅3 ⋅ ...n
4 6! = 6 . 5!
(n + 2)! = (n + 2) (n + 1)!
Ejemplo: 6! = 1 . 2 . 3 . 4 . 5 . 6 = 720 (n – 3)! = (n – 3) (n – 4)!
4! = 1 . 2 . 3 . 4 = 24
n! = 1 . 2 . 3 …………. (n – 2) (n – 4. n! = n(n – 1) (n – 2) … (n – k + 1) (n – k)!
1)n “k” multiplicaciones indicadas
Donde: n – k ≥ 0
Por definición: 1! = 1
Por convención:0! = 1 Ejemplo: 7! = 7 . 6 . 5!
7! = 7 . 6 . 5 . 4!
7! = 7 . 6 . 5 . 4 . 3!
ejercicioS reSuelToS
18 ! 16 !×17 × 18
1) Simplificar: N= Como =
16 ! 16 !
Solución: Simplificando = 17 × 18 = 306
Emplearemos una de las propiedades
anteriormente descritos.
18 ! (p − q) !
Podemos escribir: N = 2) Simplificar: I=
16 ! (p − 8) !

92. Solución: 4) Calcular n: n! x 4 x 5 x 6 x 7 = 7!
(p − q) ! 1 Solución: Escribiremos el factorial de 7
I= = convenientemente
(p − 8) (p − q)! (p − 8) ⇒ n! x 4 x 5 x 6 x 7 = 3! X 4 x 5 x 6 x 7
Luego: n! = 3!
3) Simplificar: ∴n=3
a (a − 1) !
E= 5) Hallar “a” si: 720 = (a – 8)!
a! Solución:
Solución: Recordemos que 720 = (a – 8)!
a(a – 1) ! = a!, luego: Nos damos cuenta que: 720 = 6!
a (a − 1) ! Reemplazando, tenemos:
E= 6! = (a – 8)!
a!
6=a–8
a = 14
ejercicioS propueSToS
1) Para cada caso, encontrar el valor equivalente 13 ! + 12 ! + 11 !
l. M=
de: 11 !
5! 2) Simplificar:
a. =N
2!
8 ! +6 ! (n + 36 ) !
b. M= a. P=
6! (n + 35 ) !
13 ! 9 ! n(n − 1) !
c. =P b. G=
14 ! 8 ! (n + 2 ) !
21 ! − 20 ! (r − 5 ) !
d. C= c. Q=
19 ! (r − 4 ) !
15 ! − 13 ! (p + 1) !
e. K= d. N=
13 ! (p + 2) !
5 ! +1! 2 × 30 !
f. M= e. R=
0! 29 ! + 28 !
13 ! × 0 ! 13 ! × 2 ! ( x + 2) !
g. A= + f. P=
14 ! 12 ! ( x − 2) !
6 ! +7 ! +8 ! 20 ! + 22 ! − 22( 20 ! )
h. P= g. P =
5! 20 ! + 19 ! + 21 !
1! + 2 ! + 3 ! p ! (p + 2 ) !
i. J= h. R =
2! (p − 1) ! (p + 3) !
23 ! + 24 ! + 25 !
j. N=
23 ! a! b!
3) Hallar a + b, si =8
6! +7! +8! 3!
k. P=
6! 8 × 5 !×12 × n
4) Determinar en: = 5!× 4
3!
nÚmero combinaTorio
Se define como el número total de grupos que se pueden formar con “n” elementos tomados
de “k” en “k”, de modo que los grupos se diferencias por lo menos en un elemento.
n n
NOTACIÓN: C k
∨ 
k
 

93. Sistema de Inecuaciones Cuarto Año
Se lee: combinaciones de “n” elementos tomados de k en k, o simplemente combinaciones de
n en k.
n n! Ejemplo:
DEFINICIÓN: C k
=
(n − k ) ! k ! 9 9⋅8⋅7 ⋅6⋅5⋅ 4
C 6
=
1⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6
= 84
Donde: n, k ∈ Z ; n ≥ k ≥ 0 7 7⋅6⋅5⋅4
Además: n es el índice superior C4 = 1 ⋅ 2 ⋅ 3 ⋅ 4 = 35
k es el índice inferior
2) Combinatorios Complementarios
EJEMPLOS: n n
C k
= Cn −k
9 9! 9×8× 7 × 6 !
C 6
=
(9 − 6) ! 6!
=
3!×6 !
= 84 Ejemplo:
8 8⋅7⋅6 8
C =C5
1⋅ 2 ⋅ 3
= 56
3
=
7 7! 7 × 6× 5× 4 !
C =
(7 − 4) ! 4!
=
3 !× 4 !
= 35 9 9 9 ⋅8⋅ 7
C6 = C3 = 1 ⋅ 2 ⋅ 3 = 84
4
5! 10 10 10 ⋅ 9
6
C6 = 0 ! 5!
=1 ∴
n
Cn = 1 C8 = C2 = 1 ⋅ 2 = 45
Observación: Se recomienda usar
n n! n
C1 = (n − 1) ! 1!
=n ∴
n
C1 = n esta propiedad cuando K >
2
.
n
= 1 , ∀ n ∈ Z+ 3) Suma de combinatorios
PROPIEDAD: C 0 n n n +1
C =C =C k k +1 k +1
20
C = 20 7 7 8
Ejemplos: 0 Ejemplo: C +C = C 2 3 3
42
C = 42 20 20 21
1 C +C = C 7 6 7
10
C 0
=1
4) Degradación de índices
40
C =1
C
n n n −1
k Ck −1
0
k
=
17
C 1
= 17
10 910 9
C
17
0
=1 Ejemplo: C 5 C4 = 2 C4
5
=
12 12 11 11
PROPIEDADES: C4 = 4 C3 = 3C3
Resultados importante:
Sean: n, k ∈ Z+ ; n ≥ k:
n n
n n ( n −1)(n − 2).........(n − k +1) 1- C =C0 n
= 1 ; n ∈ Z+
1) C =
1 ⋅ 2 ⋅ 3............... k
= n ; n ∈ Z+ − {1}
k n n
2- C =C
1 n −1

94. ejercicioS reSuelToS
n −5 Reemplazando:
C 7
= 16 x +1 9
1) Hallar n:
C
n −8
4
C 5
= C5
Identificando términos: x+1=9
Solución: ∴x=8
Efectuando, obtenemos:
(n −5) ! 9 9 10 11 12
(n − 5 −7) ! 7 !
3) Hallar S: S = C +C +C +C +C
2 6 6 6 6
=16 Solución:
(n −8) ! 9 9 10 11 12
(n − 8 − 4) ! 4 ! S = C 2
+ C 6
+ C 6
+ C 6
+ C 6
9
C 7
4 ! (n − 5) ! (n − 12 ) ! 10
(n −1 2 ) ! 7 ! (n − 8) !
=16 C 7
11
C 7
12
4 ! (n − 5) (n − 6 ) (n − 7 ) (n − 8 ) !
=16 C 7
7 × 6 × 5 × 4 ! (n − 8 ) ! ∴C +C
12 12 13
7 6
= C 7
(n − 5) (n − 6 ) (n − 7 ) = 7 × 6 × 5 ×1 6 x x
4) Calcule x: C 29
= 10 C30
Solución:
Desarrollando, se tiene:
(n − 5) (n − 6 ) (n − 7 ) = 1 6 ×1 5 ×1 4
x! x!
= 10
29 ! ( x − 29) ! 30 ! ( x − 30) !
x! 10
Si igualamos los términos que indican las =
29 ! ( x − 29) ( x − 30) ! 29 ! 30 ( x − 30) !
flechas, obtenemos: n = 21
1 10 1
x x 9
= =
2) Halle x: C +C = C
4 5 5
x − 29 30 3
Solución: ⇒ x − 29 = 3 ⇒ x = 32
De las propiedades, nos damos
x x x +1
cuenta: C +C = C
4 5 5
DeSarrollo Del binomio De newTon
Sea P(x ; y) = (x + y)n , n ∈ Z+, y recordemos que:
(x + y)2 = x2 + 2xy + y2
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
(x + y)5 = ?
.
.
.
(x + y)n =
⇒ El objetivo de éste capitulo es encontrar las potencias del binomio (x + y) cuando n ≥ 5.
Para ello vamos a estudiar 2 métodos o formas de poder conocer el desarrollo de (x + y)n:

95. Sistema de Inecuaciones Cuarto Año
EL TRIÁNGULO DE PASCAL
Analicemos las primeras potencias de (x + y) y escribamos solamente sus coeficientes en el
siguiente esquema triangular. Para ello consideremos (x + y) ≠ 0:
( x + y)° = 1
( x + y)1 = 1 1
( x + y) = 2
1 2 1
( x + y) = 3
1 3 3 1
( x + y) 4 = 1 4 6 4 1
( x + y) = 5 1 5 10 10 5 1
( x + y) 6 = 1 6 15 20 15 6 1
. .
. .
. .
¿Qué observamos?
Observamos que cada elemento (coeficiente) que está dentro del triángulo resulta de sumar
los elementos que están encima de el, y el primero y el último de cada potencia es 1.
Procediendo de esta manera podemos conocer:
(x + 7)7 = 1 7 21 35 35 21 7 1
Por otro lado, observando los desarrollos de (x + y)n; n = 2; 3; 4 estos son polinomios
homogéneos completos y ordenados (en forma decreciente respecto a la primera variable y en
forma creciente a la segunda). Por lo que ahora si podemos conocer el desarrollo de P(x ; y)
= (x + y)n, cuando n ≥ 5.
Veamos el caso particular de P(x ; y) = (x + y)7:
(x + y) 7 = x7 + 7x6y + 21x5y2 + 35x4y3 + 35x3y4 + 12x2y5 + 7xy6 + y7
MÉTODO DE LOS COEFICIENTES BINOMICOS
Analicemos los coeficientes en el desarrollo de (x + y)4 y (x + 5)5:
(x + y)4 = 1 4 6 4 1
↑ ↑ ↑ ↑ ↑
4 4 4 4 4
C 0 C 1 C 2 C 3 C 4
Luego, el desarrollo de (x + y)4 puede escribirse como:
4 4 4 4 4
( x + y) 4 = C0 x 4 + C1 x 3 y + C2 x 2 y 2 + C3 xy3 + C4 y 4
De manera similar
5 5 5 5 5 5
( x + y )5 =
C0 x 5 + C1 x 4 y + C2 x 3 y 2 + C3 x 2 y 3 + C4 xy 4 + C5 y 5
Con todo lo anterior, podemos enunciar el siguiente teorema:
Dado el polinomio P(x ; y) = (x + y)n , n ∈ Z+, el desarrollo de P(x ; y) es:
n n n n
( x +y) n =C0 x n +C1 x n − y +
1
............ + n − xy n − +Cn y n
C 1
1

96. Donde los números combinatorios son llamados coeficientes binomiales.
Ejemplo: Halle el desarrollo de (x + y)6
6 6 6 6 6 6 6
( x + y)6 =
C0 x 6 + C1 x 5 y + C2 x 4 y 2 + C3 x 3 y 3 + C4 x 2 y 3 + C5 xy 5 + C6 y 6
PROPIEDADES
Sea P(x ; y) = (x + y)n , n ∈ Z+
1) El desarrollo es un polinomio homogéneo, completo y ordenado de grado “n”.
2) El número de términos del desarrollo es (n + 1)
3) Los coeficientes de términos equidistantes de los extremos son iguales.
4) La suma de coeficientes del desarrollo es 2n.
∑coef (P(x ; y)) = 2n
Ejemplo:
(x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5
Notamos que: GRADO = 5
NÚMERO DE TÉRMINOS = 6
∑coef. = 32 = 25
Observación:
1. Si el binomio es (x – y), luego la ∑coef. del desarrollo de (x – y)n es CERO.
Veamos para el caso de (x – y)5:
(x – y) 5 = x5 – 5x4 + 10x3y2 – 10x2y3 + 5xy4 – y5
∑coef. = 1 – 5 + 10 – 10 + 5 – 1 = 0
2. En P(x ; y) = (x + y)n, si hacemos x = 1 ∧ y = 1, tenemos:
n n n
P(1 ; 1) = (1 + 1)n = C0 + C1 + .............. + Cn = 2
n
Ahora, si hacemos: x = 1 , y = -1:
n n n n
P(1 ; -1) = (1 – 1)n = C − C + C ................. ± C = 0
0 1 2 n
n n n n n n
⇒
C0 + C2 + C4 + ................... = C1 + C3 + C5 + ...........
TÉRMINO GENERAL
• Contando de izquierda a derecha:
n
t k +1 = Ck x n −k y k
Donde t k +1 es el término de lugar (k +1)
Ejemplo:
En el desarrollo de P(x) = (x2 + 2y3)6 determina el tercer término.
Solución:
6 6
t 3 = t 2 +1 C 2 ( x 2 ) 4 ⋅ ( 2 y 3 ) 2 = 4 C 2 x 8 y 6
• Contando de derecha a izquierda:
n
t k +1 = Ck x k y n − k
Ejemplo:
En el desarrollo de Q(x) = (x3 – 2y6)5 determine el término de lugar 4 con respecto al final.
Solución:
5 5
t 4 = t 3+1 = C3 ( x 3 )3 (−2 y 6 ) 2 = 4 C3 x 9 y12
←
TÉRMINO CENTRAL
Sea P(x ; y) = (x + y)n

97. Sistema de Inecuaciones Cuarto Año
• Si n es par: el desarrollo del binomio tendrá un único término central, el lugar que
n n
n n
+ 1 , luego: t c = t  n +1  Cn 2 x y
2 2
ocupa es  
2 2 
• Si n es impar: el desarrollo del binomio tendrá dos términos centrales, los lugares que
ocupa son:
n +1 n + 3
∧
2 2
ejercicioS reSuelToS
1) Hallar el 5to término en el desarrollo de: (x + y)7
Solución:
7
n = 7 , k = 4 ⇒ t 5 = t 4 +1 = C 4 x 7 − 4 y 4
7× 5× 6
t5 = × x 3 y 4 = 35x 3 y 4
1× 2 × 3
2) Indicar el penúltimo término de la expansión de (x2 – 1)8
Solución:
8
n = 8 , k = 7 ⇒ t PEN = t 8 = C7 ( x 2 )8 − 7 (−1) 7
t pen = −8x 2
10
 1 
3) Indicar el término independiente en el desarrollo de:  x 6 +



 x4 
Solución:
n = 10
k
10 6 10 − k  1 
t k +1 = C k ( x ) ⋅ 4 
x 
10
t k +1 = Ck x 60 − 6 k ⋅ x − 4 k
10
t k +1 = Ck x 60 −10 k
* Para que el término sea independiente, no debe tener ninguna variable, sólo el
coeficiente. Por lo cual:
60 – 10k = 0 → k = 6
10 ⋅ 9 ⋅ 8 ⋅ 7
10
⇒ t IND = C6 = = 210
1⋅ 2 ⋅ 3 ⋅ 4
problemaS para la claSe
1) Hallar el término central en el desarrollo  
14
10 3) En el desarrollo del binomio x − 1 

 3 b  x

de:  4a − 
 8 ¿Qué lugar ocupa el término de 2do
grado?
2) Calcular la siguiente suma:
7 7 7 7
S = C0 + C1 + C2 + .... C7

98. 4) Señale el valor del término del extremo final en el desarrollo de
independiente del desarrollo de: (a2 + 2b)17?
9
 x2 3 
 12) ¿Qué valor toma “n” en: (x11 + x-2)17 de
 3 + 4 modo que el producto de los términos
 
centrales sea constante?
5) Señale el coeficiente de término de
77 76
grado 7 en el desarrollo de (x7 + x-7)7. 13) Si: 3 Cn = 11Cn −1 , hallar: (n / 7) !
6) Hallar el término independiente en el 10 11
4n 4 C3 + 5 C4
 1 14) Simplificar:
desarrollo de:  x 3 +  , n ∈ Z+. 10 C5
9
 x
15)Usando propiedades, simplificar:
7) Determine “m + n”, si el 4to término del 13 14 14 13
desarrollo de: n
(x + 2) es 80x . m
K=
C C +C C
5 10 5 8
16 12 16 12
8) Hallar el valor de “m”, si el cuarto C C C C
6 4 10 7
término del desarrollo de (a – b)m 2
contiene la décima potencia de “a”. 16) Señale el término independiente de “x”
9
 0,5 x 2 
 1
n
en el desarrollo de;  + 
 x 0,5 
9) En el desarrollo de:  3x 3 +  ; la  
 x
suma de coeficientes de su desarrollo es n ! + (n + 1) ! + (n + 2) !
234. ¿Qué lugar ocupa un término que 17) Simplificar: n ! + (n + 1) !
contiene a “x” elevado a un exponente
igual al número de su lugar?
18) Determine el coeficiente del término
central de: P(x , y) = (x + 2y)6
10) ¿Cuántos términos posee el desarrollo
de (x3 + x-n)n sabiendo que 2 de sus
19) En el desarrollo de (1 + x)45 sólo los
términos consecutivos contienen “x” y x
coeficientes de los términos de lugares
respectivamente?
(2n + 1) y (n + 2) son iguales. Halle “n”.
11) ¿Cuál es el coeficiente del
20) Determine el valor de “x”, si el tercer
antepenúltimo término, contado a partir
término es doble del sexto término en el
desarrollo de: (2x + 1)7.
problemaS para la caSa
1) Calcular “x“ en: e) N.A.
x x −1 x −2
C +C
2 2
+ C2 = 136
3) Resolver:
a) 9 b) 10 x x x
c) 11 d) 8 e) N.A. 2 C4 = 2 C3 − C2
a) x = 4 b) x = 5
c) x = 9 d) x = 6 e) a
2) Resolver el sistema: yb
 x = x
C y +1 Cy −1 4) Calcular el término independiente en el
 x 21 x desarrollo de: (-3 + 2x2)5
C y = C y − 2 a) 6(3)5
b) 9(3)2
 10 c) 27 d) -5(3)5 e) N.A.
a) x = 10 ∧ y = 5
b) x = 12 ∧ y = 6 5) Calcular “n” en:
c) x = 10 ∧ y = 6 2n! – (n – 1) (n – 1)! = 6! + 5!
d) x = 9 ∧ y = 3 a) 6 b) 5

99. Sistema de Inecuaciones Cuarto Año
c) 4 d) 9 e) 8 14
 1 
x − 
x +1 y +5  x
6) Si se cumple: C y
= C4 .
a) 9 b) 8
Calcular: (x + y) c) 7 d) 6 e) 5
a) 20 b) 12
c) 3 d) 13 e) 15 22
 3
12) Si en el desarrollo de:  2 x 2 + 
7) Hallar el término independiente en el  x
desarrollo de: existe un término de la forma: αx2,
6
x 3 ¿Qué lugar ocupa dicho término?
 −  a) 5 b) 7
3 x c) 6 d) 8 e) 9
a) -15 b) -12
c) -20 d) 13 e) 20 13) Calcular el coeficiente del sexto término
del desarrollo de : (x + 2y)n,
8) Determine el tercer término en el sabiendo que su quinto término es:
desarrollo de: (x + 3)n, si se sabe que k
su cuarto término es 270xa.
2k C4 x k − 4 y 4
a) 90x3 b) 30x3 a) 1700 b) 1792
c) 60x2
d) -90x3 e) c) 1692 d) 1600 e)
N.A. -17792
24 24 14) Hallar n + k, si se sabe que el cuarto
9) Resolver: C x2
= C2 x
término del desarrollo de (x + 2y)n es
a) 5 b) 3 80xk.
c) 1 d) 2 e) 6 a) 3 b) 4
10) Calcular el término independiente en el c) 5 d) 6 e) 7
9
 1 
desarrollo de:  x +  15)Hallar el valor de n, sabiendo que:
4
 x n ! (n ! − 3)
a) 80 b) 84 = 18
c) -84 d) 81 e)-81 n!+4
a) 4 b) 8
11) Calcular el lugar del término que c) 12 d) 16 e) N.A.
2
contiene a x en el desarrollo de:
binomio De newTon
Deducción del binomio de newton para exponentes naturales.
Si multiplicamos el binomio (a+b) entre si, tomando 1, 2, 3,…………., n factores, se obtiene lo
siguiente
n = 1 ⇒ ( a + b) 1 = a + b
n = 2 ⇒ ( a + b ) 2 = a 2 + 2ab + b 2
n = 3 ⇒ ( a + b ) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
n = 4 ⇒ ( a + b ) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4
n = 5 ⇒ ( a + b ) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
Los coeficientes se pueden obtener formando el triangulo de Pascal o de Tartaglia.
1
( a + b) 0 ⇒
( a + b)1 ⇒ 1 1
( a + b) 2 ⇒ 1 2 1
( a + b) 3 ⇒ 1 3 3 1
( a + b) 4 ⇒
( a + b) 5 ⇒

100. 1 4 6 4 1
1 5 10 10 5 1
Termino general de lugar (k+1)
( )
T (k +1) = n an −k .bk
k
 n
Siendo  k  el coeficiente binomial
 
 n  = n(n − 1)(n − 2)..........(n − k + 1)
 k 
  k!
Ejemplos
5×4×3 5×4×3
i)  5  =
3
 
= = 10
3! 1× 2 × 3
8×7×6×5
ii)  8  =
5
  1× 2 × 3 × 4 × 5
= 14
Representación del desarrollo del Binomio de Newton mediante coeficientes binomiales
n n n n
(a + b) n =  a n +  a n −1 .b +  a n − 2 .b + ...... +  b n
0 1  2 n
       
Siendo el término de lugar “k+1”
n 
Tk +1 =  a n −k .b k
 
k 
n
Donde   = Cn
k k Combinaciones de “n” en “k”
 
n!
Cn =
k
(n − k )!.k!
En el cual n! es el factorial de n
n! = n(n-1) (n-2) (n-3)…………….1 .
n
Propiedades de  
k
 
Para n ∈Ν , Κ∈Ν
n 8
1)   = 1
0 ⇒ Ejemplo   = 1
0
   
n 7
2)   = 1
n ⇒ Ejemplo   = 1
7
   
n  y  7 7
3)   = 
k  n − k 
 ⇒ Ejemplo   =  
 1  6 
       
También
Si la base del binomio es una diferencia, los términos del desarrollo serán alternados (positivos
los de lugar impar y negativos los de lugar par)

101. Sistema de Inecuaciones Cuarto Año
(a-b)n = + , - , + , - , + , - , + , ……………………..
problemaS para la claSe
16
 1 
1. En:  3 − x 2  ; Hallar el 7mo Término 14
x   1
10. Hallar el tercer término de  c 2 − 
 c
2. Hallar el 5to Término de: (1 + a ) 35
11. Hallar el término de lugar 4 de:
( x-y ) 10
3. Hallar el término central del desarrollo
de: (a 3 − b 3 )16 12. Hallar el término de lugar 15 en:
( m-n ) 18
4. Hallar el grado relativo a “x” del término
de lugar 28 en el desarrollo de: 13. Hallar el 5to término en el desarrollo de:
(2 x + 3 x ) 35 ( 3x2+2y3 ) 6
14. Hallar el 8vo término del desarrollo de:
5. Hallar el grado relativo a “x” del término
( 5x3+3y2 ) 10
central en el desarrollo de:
40
 7 1  15. Hallar el 9no término del desarrollo de
x +
 
 ( 2x4+3y3 ) 11

4
x9 
16. Hallar el 3er término de: ( 2x4+3y2 ) 5
12!+13!+14!
6. Simplificar: S= 17. Hallar el término central de: ( 2x2+3y ) 4
12!+13!
18. Hallar el término central de:( 2n2+m3 ) 10
7. Hallar el grado relativo a “x” del décimo
12
término del desarrollo de: 2 3
(a-b )15 19. Hallar el término central de:  + 
a b
8. Hallar el coeficiente del séptimo término
de: (2+x) 9 20. El 5to término del desarrollo de:
7
 1 1 
9. Hallar el grado absoluto del término  2 + 2
x
 y 
central de: ( x
3
+ y 7 )8
problemaS para la caSa
1. Hallar el 4to término de: ( x 4 + 3y 5 )10
( 2 x + 3y )
2 4 5
A) 405x y
2 32
B) 405x 16 y 32
4 4 4 10
A) 1080 x y B) 1080x y 32 2 16 16
C) 405x y D) 405x y
4 12 4 12
C) 1080x y D) x y 4 4
E) 405x y
E) 1080 x y
4. Hallar el término central de: (x 2 − y 3 )8
2. Hallar el 6to término de: (3x + 2 y )
2 3 7
A) 70 x 4 y 8 8 8
B) 70 x y
Ver cual es el grado absoluto. 8 12 12 8
A) 20 B) 21 C) 70 x y D) 70 x y
C) 23 D) 22 3 4
E) 70 x y
E) 10
5. Hallar el término central de: (a − b )
3 3 4
3. Hallar el tercer término del desarrollo de:

102. A) 6a 6 b 6 B) 6a 4 b 4 C) 720 x 3 D) 720 x 9 E) 720 x
C) 6a 3 b 3 D) 6a 4 b 5
11. Calcular el término central del desarrollo
E) 6a 5 b 4 10
 1 
de: x + 2 
 x 
6. Hallar el término central de: (3a − b ) 6 252
A) 252 x 5 B)
A) − 540a 3 b 3 B) − 540a 4 b 4 x5
C) − 540b 2 D) − 540a 2 252
C) D) 252 x 8 E) 252 x
E) − 540b 6 x3
7. Hallar el término de lugar 5 en: 12. Hallar el término que contiene a x8 en el
desarrollo de: ( x+y ) 13
(x 2 + y 3 ) 6 8 3 8 8
2 3 4 12 A) 1287 x y B) 1287 x y
A) 15x y B) 15x y 8 5 8 6
12 3 12 12 C) 1287 x y D) 1287 x y
C) 15x y D) x y E) 15x y 8 10
E) 1287 x y
8. Hallar el término de lugar 10 en:
13. Hallar el valor de x de tal manera que la
( x 2 − y 3 )10
suma del 3ro y 5to término en el
10 4 10 6
A) x y B) 85x y desarrollo de ( x+1 ) 4 sea igual a 25
10 16 12 A) ±1 B) ±2
C) 48x y D) 56 x y E) N.A.
C) ±3 D) ±4 E) 5
9. Calcular el término central del desarrollo 14. El último término en el desarrollo de:
de: (a + 2 b ) 8 ( x - 3y ) 5
A) − 15 y B) − 15 y
5 5
A) 1120a 2 b 2 B) 1120a 4 b 4
C) 1120a 3 b 3 D) 1120a 8 b 8 E) N.A. C) − 15 y
5
D) − 15 y
5
E) − 15 y
5
10. Calcular el tercer término del desarrollo 15. Cual es el coeficiente de x14 en el
de: (2 x + 3) 5 desarrollo de: ( x2+x3 ) 6
A) 720 x 2 B) 720 x 31 A) 12 B) 18
C) 15 D) 21 E) 24