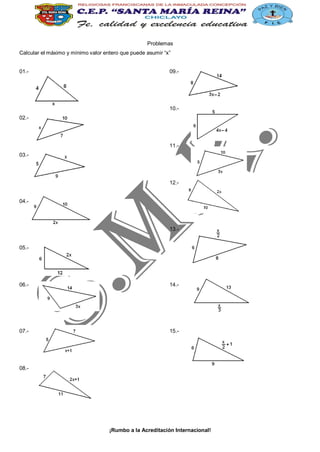
Este documento presenta una serie de problemas de geometría sobre triángulos y sus elementos (lados, ángulos, alturas, bisectrices) para ser resueltos. Los problemas cubren temas como cálculo de ángulos, lados y perímetros de triángulos dados ciertas condiciones sobre sus elementos. El documento contiene 24 problemas de este tipo agrupados en secciones como "Desafío", "Teoremas Fundamentales Básicos", y "Propiedades Adicionales".

1. ¡Rumbo a la Acreditación Internacional!
Problemas
Calcular el máximo y mínimo valor entero que puede asumir “x”
01.-
02.-
03.-
04.-
05.-
06.-
07.-
08.-
09.-
10.-
11.-
12.-
13.-
14.-
15.-

2. Elisban Jeffersson Vivanco Gonzales Página 2
Geometria
DESAFIO
01.- En el triángulo ABC, “” es obtuso, ¿Cuáles son
valores enteros de “x”?
a) 5,7,8
b) 6,7,8
c) 7,8,9
d) 9,10,11
e) NA
02.- En el gráfico, ¿Cuántos valores enteros admite
“x”?
a) 6
b) 7
c) 8
d) 9
e) 10
03.- En el triángulo ABC un lado es la mitad de otro.
Calcular el perímetro del triángulo.
a) 21 ó 28
b) 18 ó 24
c) 16
d) 20
e) 23
04.- Los lados de un triángulo son enteros, dos de
ellos son 7 y 9, calcular el mínimo valor entero del
tercer lado.
a) 2 b) 3 c) 5 d) 4 e) 6
05.- Los lados de un triángulo miden 14; x-4 y x+6.
Calcular el menor valor entero que puede tomar “x”.
a) 5 b) 6 c) 7 d) 8 e) 9
TEOREMAS FUNDAMENTALES BÁSICOS
PROBLEMAS

3. Elisban Jeffersson Vivanco Gonzales Página 3
Geometria
09.- En el gráfico, calcule x – y
a) 15º
b) 20º
c) 25º
d) 30º
e) 35º
10.- Hallar “x”
a) 10º
b) 20º
c) 25º
d) 30º
e) 15º
11.- Hallar “x”
a) 10º
b) 20º
c) 25º
d) 30º
e) 15º
12.- Hallar “x”
a) 10º
b) 20º
c) 25º
d) 30º
e) 15º
13.- Hallar “x”.
a) 16°
b) 12°
c) 15°
d) 10°
e) 24°
14.- Hallar “x”
a) 100°
b) 110°
c) 95°
d) 107°
e) 105°
15.- En un triangulo ABC, mA=82º24’54’’ ;
mB=34º56’18’’. Hallar mC
a) 60º30’30’’ b) 64º34’46’’ c) 62º38’48’’
d) 62º e) 62º30’
16.- ¿Cuánto mide uno de los ángulo agudos de u
triangulo rectángulo isósceles?
a) 15° b) 30° c) 37° d) 45° e) 60°
17.- Encontrar el valor de “x”.
a) 60°
b) 55°
c) 45°
d) 65°
e) 50°
18.- En el gráfico calcular “x”
a) 25º
b) 30º
c) 35º
d) 40º
e) NA
19.- Hallar “x”
a) 9°
b) 10°
c) 12°
d) 15°
e) 18°
20.- Hallar “x”
a) 15°
b) 10°
c) 25°
d) 40°
e) 45°
21.- Hallar “x”
a) 10º
b) 11º
c) 12º
d) 15º
e) 18º
22.- Calcular “x”
a) 15° b) 30° c) 24° d) 18° e) 20°
23.- Calcular “++”
a) 360° b) 720° c) 540° d) 900° e) 1080°

4. Elisban Jeffersson Vivanco Gonzales Página 4
Geometria
24.- Hallar “x”
a) 100° b) 110° c) 120° d) 130° e) 140°
PROPIEDADES ADICIONALES
EJERCICIOS
01.- Hallar “x”
02.- Hallar “x”
03.- Hallar “x”
04.- Hallar “x”
05.- Hallar “x”
06.- Hallar “x”
07.- Hallar “x”
08.- Hallar “x”
09.-
10.- En un triángulo isóseles ABC (AB=BC) se traza la
altura AH. Calcular la mHAC, si mB=80°.
a) 35 b) 40º c) 45º d) 50º e) NA
11.- En un triángulo ABC: mA = 20° y mC = 40°.
Calcular la medida del menor ángulo formado por las
alturas que parten de A y C.
a) 55º b) 45º c) 35º d) 60º e) NA
12.- En un triángulo rectángulo ABC, recto en B, se
trazan la altura BH y la bisectriz interior AD, las cuales
se intersectan en P. Si BP=6 y DC=13, Calcular BC.
a) 15 b) 16 c) 19 d) 20 e) NA
13.- En un triángulo rectángulo ABC, recto en B se
traza la altura BH. La bisectriz del HBC intersecta en
P a HC. Si AB=5, calcular el máximo valor entero de
BP.
a) 12 b) 9 c) 15 d) 16 e) NA
14.- El ángulo A de un triángulo ABC mide 20º. Se
traza la ceviana CT y en el triángulo ATC se traza la
cevianaTQ. Si mATQ = 40° y TQ = QC = BC.
Calcular la mB
a) 80º b) 70º c) 10º d) 65º e) NA