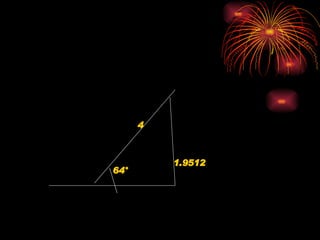
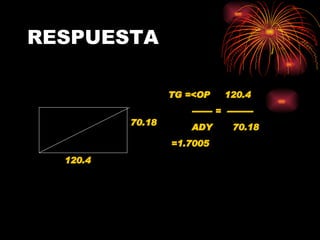
El documento presenta información sobre trigonometría y el Teorema de Pitágoras. Explica conceptos como ángulos, funciones trigonométricas, el problema básico de la trigonometría y cómo resolverlo mediante el uso de un teodolito. También incluye ejemplos de cálculos trigonométricos, tablas de funciones trigonométricas y ejercicios resueltos sobre el Teorema de Pitágoras.

1. PRESENTACION JOHANA ABIGAIL MEDELLIN GUILLEN N.L.37 YESSICA JAZMIN IBARRA DE LEON N.L:20

2. INTRODUCCION EN ESTE TRABAJO TE PRESENTAMOS TODO SOBRE EL TEMA DEPITAGORAS Y TRGONOMETRIA DE QUE COMO SE REALIZAN LOS PROBLEMAS ,DE CÓMO ENCONTRAR LOS ANGULOS , SACAR LA HIPOTENUSA ,SAR LOS LADOS DE CATETO AYDESENTE TAMBIEN BIENE UNOS EJERCICIOS DE TODOS LOS TEMAS UNA AUTOEVALUACION ASI COMO TAMBIEN BIENE LO QUE SIGNIFICA PITAGORAS COMO SE REALIZA, EL TEOREMA Y COMO PODER USAR EL TEOREMA TAMBIEN BIENE LA PRSESNTACION QUE CONTIENE EL NOMBRE DE QIEN REALIZO EL TRABAJO ASI TABIEN BIENE DE CÓMO REALIZAR LOS ANGULOS ,BIENE TAMIEN LOS EJERCICIOS . ASI TAMBIEN LO QUE SIGNI FICA TRIGONOMETRIA COMO SE REALIZA COMO TMBIEN DICE LOS PASOS DE REALIZAR LOS EJERCICIOS .

3. TRIGONOMETRIA El problema básico de la trigonometría es algo parecido a esto: Está cerca de un ancho río y necesita conocer la distancia hasta la otra orilla, digamos hasta el árbol marcado en el dibujo por la letra C (para simplificar, ignoremos la 3ª dimensión). ¿Cómo hacerlo sin cruzar el río? La forma habitual es como sigue. Clave dos postes en el suelo en los puntos A y B y mida con una cinta la distancia c entre ellos (la "base").

4. TRIGONOMETRIA Luego extraiga el poste del punto A y sustitúyalo por un telescopio de topógrafo como el que se muestra aquí ("teodolito"), contando con una placa dividida en 360 grados, marque la dirección ("azimut") a la que apunta el telescopio. Dirigiendo el telescopio primero hacia el árbol y luego hacia el poste B, mide el ángulo A del triángulo ABC, igual a la diferencia entre los números que ha leído de la placa de azimut. Sustituya el poste, lleve el teodolito al punto B y mida de la misma forma el ángulo B .

5. TRIGONOMETRIA Signos de las funciones trigonométricas De acuerdo con el cuadrante en que se halle el lado terminal del ángulo y teniendo en cuenta que la distancia de un punto cualquiera al origen de coordenadas es siempre positiva, y aplicando la "ley de los signos", las funciones trigonométricas pueden ser positivas o negativas. En la tabla de la parte inferior se resumen los signos de las funciones trigonométricas en cada uno de los cuadrantes.

6. TRIGONOMETRIA Sabiendo que sen A = 4/5, calcula las demás razones trigonométricas de A sabiendo que es un ángulo del segundo cuadrante. 2º Sabiendo que cos A = -raiz(3)/2, sin utilizar la calculadora, obtener las demás razones trigonométricas de A, y el ángulo A, sabiendo que está en el segundo cuadrante. 3º Sabiendo que cos A = -1/2, sin utilizar la calculadora, obtener las demás razones trigonométricas de A, y A, sabiendo que es un ángulo del segundo cuadrante. 4º Sin utilizar la calculadora, obtener las razones trigonométricas de 315º. 5º Sin utilizar la calculadora, obtener las razones trigonométricas de 240º. 6º Sin utilizar la calculadora, obtener las razones trigonométricas de 300º

7. ENCUENTRA EL SIGUIENTE ANGULO: 45 28 53

9. RESPUESTA: SENO DEL ANGULO A:C.OP.= HIPO. 28 — =0.5283 =50 ° 53 HIPO.

10. COS. DEL ANGULO A: ADY. HIPO. 45 —— =0.8490 =50 ° 53

11. TG. DEL ANGULO A:C.OP. ADY. 28 — =0.6222 53

12. EJEM´PLOS DE PITAGORAS: TG. DE 20 °24´= 0.3706 +0.0013 ——―—— 0.3719 0.0436 COS. DE 87°39`=–0.0026 ——––— 0.0410

13. COS. DE 45 °18`= 0.7050 -0.0017 ———— 0.7033 CONTG. DE 37°22` = 1.311 -0.002 ———— 1.309

14. H SEN. DE 75°17` = 0.9689 +0.0005 ――――― 0.9694 TG. DE 19°29` = 0.3508 +0.0029 ———— 0.3479

15. TG. DE 10 °51` = 0.1914 +0.0003 ———— 0.1917 COS. DE 1°45` = 0.9996 -0.0000 ———— 0.9996

16. CONTG. DE 38 °38 = 1.257 -0.006 ———— 1.251 SEN. DE 59°57 = 0.8646 +0.0010 ———— 0.8656

17. LOCALIZA LOS SIGUIENTES ANGULOS: SEN DEL ANGULO B =OP H 5 — = 0.5681 8.8 TG DEL ANGULO A= OP 9.4 — = — =0.5222 ADY 18

18. COS DEL ANGULO B= ADY 6 —— = — H 6.8 = 0.8823 TG. DEL ANG. C= OP 2 —— =― = 1.11 ADY1.8 SEN DEL ANG. A= OP 17.3 H = —— = 0.7723 22.4

19. COS DEL ANG.B=ADY= 34 H —=1.8888 18 TG DEL ANG.C=OP= 56.9 ADY ——=1.156 49.2 TG DEL ANG.A=OP =1.8 ADY ——=0.4 4.5 SEN DEL ANG.B= OP=2.5 H ——=0.5 5 88

20. COS DEL ANG.C=ADY= 4 H —=0.49 8.1 COS DEL ANG.A=ADY= 5 H —=2.7777 1.8 TG DEL ANG.C= OP = 34 ADY — = 1.8994 17.9

21. SEN DEL ANG . A= OP= 10.5 H —=1.4383 7.3 COS DEL ANG. C= ADY= 6.7 H —= 0.7613 8.8 SEN DEL ANG.C OP= 13.7 H ——=1.5054 9.1

22. LOCALIZA 5 ANGULOS EN LA TABLA TRIGONOMETRICA CONTG. DEL ANG.25 °27`=2.101 SENO DEL ANG.64°52`=0.9054 TAN. DEL ANG.49°=1.150 COS DEL ANG.44°21`=0.7151 COS DEL ANG.17°59`= 0.9152

23. LOCALIZA 5 EJEMPLOS DEL TEMA DE PITAGORAS 10 5 H2= C2+C2 H=(5)2+(10)2 H=25+100 H=125 H= 11.1

24. 9.8 10.5 C2=H2-C2 C=(10.5)-(9.8)2 C=110.25-96.04 C=14.21 C=3.76

25. H2=C2+C2 H=(25.6)2+(39.8)2 H=655.36+1584..04 H=2239.4 H=47.3

26. C2=H2-C2 4 8.5 C=(8.5)2-(4)2 C=72.25-16 C=56.25 C=7.5

27. 4.9 21 H2=C2+C2 H=(4.9)2+(2.1)2 H=24.01+4.41 H=28.42 H=5.3

28. RESUELVE LOS SIGUIENTES ANGULOS Y RESUELVELOS. 8.9 8 SEN=OP 8 -------=-----=0.8988=64 ° H 8.9 ADYASENTE TG=64 °=OP ----- ADY (TG 64)(ADY)=8 LOCALIZA LO SIGUIENTES ANGULOS Y RESUELVELOS

29. ADY = 8 ---- TG 64 ADY = 8 ------ 2.3478 ADY=3.40

30. 4 17 76 °40` TG= OP 17 ------=------- ADY 4 HIPOTENUSA COS =76 °40`= 4 ---------- ---- 1 H

31. COS =76 °40=4 H= 4 ------ 0.2306 H=17.4

32. RESUELVE LOS SIGUIENTES PROBLEMAS RAZONADOS: CALCULAR EL LADO DE UN ROMBO CUYAS DIAGONALES MIDEN 6 Y8 CENTIMETROS. 4 3

33. RESPUESTA DEL PROBLEMA: H2= C2+C2 H=(4)2+(3)2 16+9 25 5

34. RESUELVE: RESOLBER UN TRIANGULO ISOCELES EN EL CUAL LA BASE MIDE 19.8 METROS Y LA ALTURA MIDE 12.5METROS 19.8 3 12.5

35. RESPUESTA DEL TRIANGULO ISOCELES : H2=C2+C2 H=(9.9)2+(12.5)2 98.01+156.25 H=254.26 H=15.94

36. RESUELVE: CALCULAR LA LOGITUD DE LA CUERDA QUE CORRESPONDEA UN ANGULO CENTRAL DE 64 ° EN UNA CIRCUNFERENCIA DE 4 CETIMETROS DE RADIO

37. 64 ° 4 1.9512

38. RESPUESTA DEL EJERCICIO: TG=64 °=OP ------- ADYD TG.=64°= 4 ------ ADY

39. (TG 64 °)(X)=4 X= 4 ----- 64 X=4 ------ 2.050 X=1.9512

40. RESUEVE: LA BASE DE UN TRIANGULO ISOCELES ES DE 64.5 CENTIMETROS Y EL ANGULO OPUESTO ES DE 72 °.8`. CALCULAR EL RESTO DE LOS ELEMENTOS.

41. RESPUESTA: 72.8 36.4 32.25 64.5

42. ANGULO. TG =36.4 =32.5 -------- ------- 1 x TG =36.4x =32.25 X=32.25 = 43.74 -------------- TG =36.4

43. HIPOTENUSA. H2= C2+C2 H= (32.25)2+(43.74)2 H=1040.0625+1913.1876 H=2953.2501 H=54.3438

44. RESUELVE: UNRECTANGULOPOSEE UNAS DIMENSIONES DE 120.x 70.18 METROS. DETERMINAR LOS ANGULOS QUE UNA DE SUS DIAGONALES FORMA CON LOS LADOS.

45. RESPUESTA 120.4 70.18 TG =<OP 120.4 ------- = --------- ADY 70.18 =1.7005