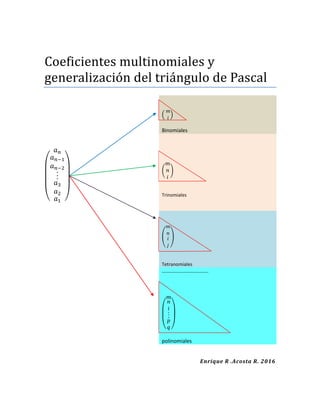
El documento explica cómo generalizar el triángulo de Pascal mediante el uso de coeficientes multinomiales. Define multinomiales como el producto de coeficientes binomiales sucesivos y muestra cómo esto permite construir triángulos de coeficientes para trinomiales, tetranomiales y polinomiales más altos como análogos del triángulo de Pascal. También resume brevemente la historia y propiedades básicas del triángulo de Pascal.

1. Coeficientes multinomiales y
generalización del triángulo de Pascal
(
𝑚
𝑖
)
Binomiales
(
𝑚
𝑛
𝑖
)
Trinomiales
(
𝑎 𝑛
𝑎 𝑛−1
𝑎 𝑛−2
...
𝑎3
𝑎2
𝑎1 )
(
𝑚
𝑛
𝑖
𝑗
)
Tetranomiales
……………………………..
(
𝑚
𝑛
𝑖...
𝑝
𝑞 )
polinomiales
Enrique R .Acosta R. 2016

2. Coeficientes multinomiales y la generalización del Triángulo de Pascal
Intentaremos en este trabajo explicar cómo se pueden construir análogos del triángulo de Pascal
( ∆ 𝟎), como una expansión de las interrelaciones entre las sucesiones paralelas constituyentes del
triángulo y al uso del concepto de multinomiales.
Definición:
Dados un sucesión de números enteros (que puede incluir al cero),{𝑎𝑖} = {𝑎1, 𝑎2, … , 𝑎 𝑛−1 𝑎 𝑛} ,
donde 𝑎1 ≤ 𝑎2 ≤ ⋯ ≤ 𝑎 𝑛−1 ≤ 𝑎 𝑛 , podemos definir un número combinatorio denominado
multinomial de dicho conjunto, como:
(
𝑎 𝑛
𝑎 𝑛−1
𝑎 𝑛−2
...
𝑎3
𝑎2
𝑎1 )
=
𝑎 𝑛!
(𝑎 𝑛 − 𝑎 𝑛−1)! (𝑎 𝑛−1 − 𝑎 𝑛−2)!… (𝑎3 − 𝑎2)! (𝑎2 − 𝑎1)! 𝑎1!
Un multinomial de n elementos, se obtiene como el producto de (𝑛 − 1 ) coeficientes Binomiales
sucesivos, así:
(
𝑎 𝑛
𝑎 𝑛−1
𝑎 𝑛−2
...
𝑎3
𝑎2
𝑎1 )
= (
𝑎 𝑛
𝑎 𝑛−1
) (
𝑎 𝑛−1
𝑎 𝑛−2
) … (
𝑎3
𝑎2
) (
𝑎2
𝑎1
) =
𝑎 𝑛!
(𝑎 𝑛 − 𝑎 𝑛−1)! 𝑎 𝑛−1!
𝑎 𝑛−1!
(𝑎 𝑛−1 − 𝑎 𝑛−2)! 𝑎 𝑛−2!
…
𝑎3!
(𝑎3 − 𝑎2)! 𝑎2!
𝑎2!
(𝑎2 − 𝑎1)! 𝑎1!
Este concepto nos ayuda a construir “triángulos de coeficientes” trinomiales, Tetranomiales,
pentanomiales, etc., y en general, para cualquier polinomio elevado a la potencia m, como
análogos, o generalizaciones del “triángulo de Pascal”
Así, un trinomial, será el producto de dos Binomiales, por ej. :
(
3
2
1
) = (
3
2
) (
2
1
) = 3𝑥2 = 6
Un tetranomial, será el producto de tres Binomiales, por ej. :
(
5
3
2
1
) = (
5
3
) (
3
2
) (
2
1
) = 10𝑥3𝑥2 = 60
Pero también un tetranomial, puede ser visto como el producto de un binomial por un trinomial,
así con los valores del ejemplo anterior, tendremos:
(
5
3
2
1
) = (
5
3
) (
3
2
) (
2
1
) = (
5
3
2
) (
2
1
) = (
5
3
) (
3
2
1
) = 60

3. Análogamente, el producto de cuatro Binomiales, puede considerarse como un pentanomial, pero
también como el producto de un binomial por un tetranomial, o como el producto de dos
trinomiales, pej. :
(
5
4
3
1
0)
= (
5
4
) (
4
3
) (
3
1
) (
1
0
) = (
5
4
) (
4
3
1
0
) = (
5
4
3
) (
3
1
0
)= 60
Estas interpretaciones pueden extenderse a cualquier orden, siempre que los elementos del
producto, estén organizados de manera que cumplan las condiciones establecidas al inicio.
TRIANGULO DE PASCA L y COEFICIENTES BINOMIALES
El triángulo que a continuación se muestra ( ∆ 𝟎) , se denomina en Occidente como triángulo de
Tartaglia (1500-1557) o más comúnmente triángulo de Pascal (1632-1662), porque su
descubrimiento es atribuido a dichos matemáticos europeos, pero ya dicha distribución de números,
aparece en la portada del Rechnung, un libro de aritmética del matemático y astrónomo alemán
Peter Apian (1499-1552), y el matemático chino Chu Shih Chien, lo mencionó en 1303 (3 siglos
antes) en su libro “El espejo maravilloso de los 4 elementos”, refiriéndose a él como el antiguo
método (usado desde 2 siglos atrás). Probablemente dicho triángulo se remonta al año 1100 d.C.,
cuando el poeta y matemático persa Omar Khayyam, parece referirse a él en su famosa álgebra.
TRIANGULO DE PASCAL ( ∆ 𝟎 ), (filas desde n=0, hasta n=8)
𝑺 𝟏 Filas
1 𝑺 𝟐 0
1 1 𝑺 𝟑 1
1 2 1 𝑺 𝟒 2
1 3 3 1 𝑺 𝟓 3
1 4 6 4 1 𝑺 𝟔 4
1 5 10 10 5 1 𝑺 𝟕 5
1 6 15 20 15 6 1 𝑺 𝟖 6
1 7 21 35 35 21 7 1 𝑺 𝟗 7
1 8 28 56 70 56 28 8 1 8
El triángulo de Pascal, se construye a partir de las sucesiones de números, constituyentes de las
series , obtenidas a partir de la relación de recurrencia:
𝑥(𝑥+1)(𝑥+2)…(𝑥+𝑚−1)(𝑥+𝑚)
1.2.3…𝑚(𝑚+1)
−
(𝑥−1)𝑥(𝑥+1)…(𝑥+𝑚−1)
1.2.3…𝑚(𝑚+1)
=
𝑥(𝑥+1)(𝑥+2)…(𝑥+𝑚−1)
1.2.3…𝑚
,

4. Nosotros hemos denotado a dichas sucesiones como : 𝑺 𝟏, 𝑺 𝟐, 𝑺 𝟑, … , 𝑺 𝒎 , donde consideramos los
primeros n términos de la sucesión, y el sub índice m, es un contador para indicar su ubicación
como serie paralela, que hacemos coincidir con el segundo término de la serie respectiva.
Cada una de estas series paralelas de n términos se caracteriza porque su término n-ésimo, es
igual a la suma de los n términos de la sucesión precedente.
La manera más usual de representar estas sucesiones, es agrupándolas en forma de un triángulo
equilátero numérico (con igual número de elementos en cada lado), y simétrico respecto a su
“altura”, en el cual estas sucesiones de números figurados, o combinatorios 𝑺 𝒎 , aparecen
repetidas en ambas direcciones oblicuas del triángulo.
El triángulo resulta ilimitado por su base y la lectura de sus filas horizontales tiene el mismo tenor,
si su lectura se hace en un sentido o en el contrario. Así mismo, cada fila inicia y termina en un
valor unitario y los restantes términos de cada fila se puede obtener de la anterior, sumando cada
dos números consecutivos de la fila anterior, siendo esto una consecuencia inmediata de que cada
serie paralela, viene a ser la serie de las diferencias primeras de la serie anterior. (Ver a modo de
ejemplo el trazado de color rojo entre fila 5 y fila 6 en el gráfico numérico del triángulo)
El triángulo de Pascal, se puede considerar horizontalmente, como la distribución de números o
coeficientes que resultan de la expansión de las potencias sucesivas de un binomio elevado a una
potencia k, como (𝑥1 + 𝑥2) 𝑘
, cuando k varia de cero a n. Las filas del triángulo se numeran de
arriba abajo, tal como sea el valor de k, y los términos de la fila n, son los coeficientes que
corresponden al desarrollo del binomio (𝑥1 + 𝑥2) 𝑛
o binomio de Newton:
(𝑥1 + 𝑥2) 𝑛
= ∑ (
𝑛
𝑖
)
𝑛
𝑖=𝑜
𝑥1
𝑛−𝑖
𝑥2
𝑖
Estos coeficientes distribuidos en filas (líneas), se denominan coeficientes binomiales y se denotan
usualmente como:
(
𝑛
𝑚
) =
𝑛!
(𝑛 − 𝑚)! 𝑚!
=
𝑛(𝑛 − 1)(𝑛 − 2) … (𝑛 − 𝑚 + 1)
1.2.3 … 𝑚
Como es conocido, la expresión (
𝑛
𝑚
), se denomina número combinatorio, y representa el n⁰ de
combinaciones que se pueden formar con los n elementos de un conjunto, tomados de m en m, de
tal manera que todos los grupos resultantes se diferencien entre sí, al menos en un elemento
(combinaciones simples, sin repetición, y por ende , el orden de los elementos en el grupo no hace
diferenciación alguna).Por conveniencia ,en lo que respecta a la nomenclatura a utilizar, para
nuestros fines, hemos incluido el valor 1 en el vértice superior del triángulo, de manera de incluir el
caso trivial (𝑥1 + 𝑥2)0
=1, correspondiente a k=0, y al combinatorio (
0
0
) = 1. Así aparece en la fila
cero (0), el coeficiente 1, como único elemento. Una identidad fundamental e inmediata de estos
números es (
𝑛
𝑚
)=(
𝑛
𝑛 − 𝑚
), implícita en su propia definición.

5. TRIANGULO DE COEFICIENTES COMBINATORIOS ( ∆ 𝟎 ) , (filas desde n=0, hasta n=8)
𝑺 𝟏
fila
(
𝟎
𝟎
) 𝑺 𝟐
0
(
𝟏
𝟎
) (
𝟏
𝟏
) 𝑺 𝟑
1
(
𝟐
𝟎
) (
𝟐
𝟏
) (
𝟐
𝟐
) 𝑺 𝟒
2
(
𝟑
𝟎
) (
𝟑
𝟏
) (
𝟑
𝟐
) (
𝟑
𝟑
) 𝑺 𝟓
3
(
𝟒
𝟎
) (
𝟒
𝟏
) (
𝟒
𝟐
) (
𝟒
𝟑
) (
𝟒
𝟒
) 𝑺 𝟔
4
(
𝟓
𝟎
) (
𝟓
𝟏
) (
𝟓
𝟐
) (
𝟓
𝟑
) (
𝟓
𝟒
) (
𝟓
𝟓
) 𝑺 𝟕
5
(
𝟔
𝟎
) (
𝟔
𝟏
) (
𝟔
𝟐
) (
𝟔
𝟑
) (
𝟔
𝟒
) (
𝟔
𝟓
) (
𝟔
𝟔
) 𝑺 𝟖
6
(
𝟕
𝟎
) (
𝟕
𝟏
) (
𝟕
𝟐
) (
𝟕
𝟑
) (
𝟕
𝟒
) (
𝟕
𝟓
) (
𝟕
𝟔
) (
𝟕
𝟕
) 𝑺 𝟗 7
(
𝟖
𝟎
) (
𝟖
𝟏
) (
𝟖
𝟐
) (
𝟖
𝟑
) (
𝟖
𝟒
) (
𝟖
𝟓
) (
𝟖
𝟔
) (
𝟖
𝟕
) (
𝟖
𝟖
) 8
Las sucesiones paralelas, se pueden expresar en términos combinatorios como:
𝑺 𝒎={(
𝒊
𝒎 − 𝟏
)} con i = (m-1),m,…,(m+n-2), para cada m=1,2,…,n ,
y su valor suma, 𝑺 𝒎
+
, corresponde a las combinaciones con repetición de n números naturales,
tomados m a m, 𝑪𝒓 𝒏,𝒎 .
Luego para m=1 , con i= 0,1,…,(n-1) resulta:
𝑆1 = {(
𝑖
0
)} = {(
0
0
) , (
1
0
) , (
2
0
) , … , (
𝑛 − 1
0
)} = {1,1,1,1,1, … ,1} , y: 𝑆1
+
= 𝐶𝑟𝑛,1 = ∑ (
𝑖
0
) = (
𝑛
1
)𝑛−1
𝑖=0
Si m=2 , con i=1,2,…,n
𝑆2 = {(
𝑖
1
)} = {(
1
1
) , (
2
1
) , (
3
1
) , … , (
𝑛
1
)} = {1,2,3,4,5,6, … , 𝑛}, y: 𝑆2
+
= 𝐶𝑟𝑛,2 = ∑ (
𝑖
1
)𝑛
𝑖=1 = (
𝑛 + 1
2
)
Si m=3, con i=2,3,…,(n+1)
𝑆3 = {(
𝑖
2
)} = {(
2
2
) , (
3
2
) , (
4
2
) , … , (
𝑛 + 1
2
)} = {1,3,6,10,15,21, … ,
(𝑛+1)𝑛
2!
},y: 𝑆3
+
= 𝐶𝑟𝑛,3 = ∑ (
𝑖
2
)𝑛+1
𝑖=2 = (
𝑛 + 2
3
)
Para m=4, con i=3,4,…,(n+2)
𝑆4 = {(
𝑖
3
)} = {(
3
3
) , (
4
3
) , (
5
3
) , … , (
𝑛 + 2
3
)} = {1,4,10,20,35,56, … ,
(𝑛+2)(𝑛+1)𝑛
3!
}, y: 𝑆4
+
= 𝐶𝑟𝑛,4 = ∑ (
𝑖
3
)𝑛+2
𝑖=3 = (
𝑛 + 3
4
)
…………………………………………………………………………………..
La expresión general será:
𝑺 𝒎 = {(
𝒊
𝒎 − 𝟏
)} = {(
𝒎 − 𝟏
𝒎 − 𝟏
) , (
𝒎
𝒎 − 𝟏
) , (
𝒎 + 𝟏
𝒎 − 𝟏
) , … , (
𝒎 + 𝒏 − 𝟐
𝒎 − 𝟏
)}={𝟏,
𝒎
𝟏!
,
(𝒎+𝟏)𝒎
𝟐!
,
(𝒎+𝟐)(𝒎+𝟏)𝒎
𝟑!
, … ,
[𝒏+(𝒎−𝟐)][𝒏+(𝒎−𝟑)]…𝒏
(𝒎−𝟏)!
},

6. y: 𝑆 𝑚
+
= 𝐶𝑟𝑛,𝑚 = ∑ (
𝑖
𝑚 − 1
)𝑛+𝑚−2
𝑖=𝑚−1 = (
𝑛 + 𝑚 − 1
𝑚
)
El triángulo de Pascal también se puede representar convenientemente, como un triángulo isósceles
rectángulo, donde las series paralelas se ubican en las columnas paralelas al cateto vertical, y en las
direcciones paralelas a la hipotenusa del triángulo, tal como se muestra a continuación:
TRIANGULO DE PASCAL (∆ 𝟎) (Valores numéricos)
𝑺 𝟏 𝑺 𝟐 𝑺 𝟑 𝑺 𝟒 𝑺 𝟓 𝑺 𝟔 𝑺 𝟕 𝑺 𝟖 𝑺 𝟗
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Notamos que en la fila 0 solo hay un elemento, en la fila 1 aparecen 2 elementos, en la dos aparecen
3 elementos, y así sucesivamente, es decir el número de elementos de cada fila, corresponde a la
sucesión 𝑆2 = {(
𝑖
1
)} = 1,2,3, … , 𝑛, con i=1,2,…,n
Análogamente, podemos representar en un triángulo isósceles rectángulo, los coeficientes
Binomiales, tal como se muestra en la figura:
TRIÁNGULO DE COEFICIENTES COMBINATORIO BINOMIALES ( ∆ 𝟎)
(
0
0
)
(
1
0
) (
1
1
)
(
2
0
) (
2
1
) (
2
2
)
(
3
0
) (
3
1
) (
3
2
) (
3
3
)
(
4
0
) (
4
1
) (
4
2
) (
4
3
) (
4
4
)
(
5
0
) (
5
1
) (
5
2
) (
5
3
) (
5
4
) (
5
5
)
(
6
0
) (
6
1
) (
6
2
) (
6
3
) (
6
4
) (
6
5
) (
6
6
)
(
7
0
) (
7
1
) (
7
2
) (
7
3
) (
7
4
) (
7
5
) (
7
6
) (
7
7
)
(
8
0
) (
8
1
) (
8
2
) (
8
3
) (
8
4
) (
8
5
) (
8
6
) (
8
7
) (
8
8
)
Donde ya se evidencia de manera inmediata, la secuencia de ordenación para los coeficientes binomiales .

7. COEFICIENTES TRINOMIALES:
En trabajos anteriores (Prisma Combinatorio), hemos establecido que dichos coeficientes se
agrupan en este caso, en lugar de en líneas, en áreas triangulares equiláteras, que hemos
denominado Triángulos de coeficientes trinomiales ∆ 𝑇, que se obtienen al multiplicar todos los
valores contenidos en cada fila de ∆ 𝟎 , hasta la potencia considerada del binomio, o fila n del
triángulo de Pascal ( ∆ 𝟎), por el valor ,de igual ubicación relativa, en la propia fila n. Veamos a
continuación algunos ejemplos:
Tabla de transformación de ∆ 𝟎, en ∆ 𝑻 (ver notas finales)
m Filas de
∆ 𝟎 / ∆ 𝑇
Elementos de cada
Fila de ∆ 𝟎
Factores de
La fila n
Resultado o triángulo de
Coeficientes trinomiales ∆ 𝑇
0 0 1 1 1
1 0 1
1 1
1
1
1
1 11
2 0 1
1 1
1 2 1
1
2
1
1
2 2
1 2 1
1
2
3 0 1
1 1
1 2 1
1 3 3 1
1
3
3
1
1
3 3
3 6 3
1 3 3 1
1
2
3
4 0 1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1
4
6
4
1
1
4 4
6 12 6
4 12 12 4
1 4 6 4 1
1
2
3
4
5 0 1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1
5
10
10
5
1
1
5 5
10 20 10
10 30 30 10
5 20 30 20 5
1 5 10 10 5 1
1
2
3
4
5
Notamos que en la primera fila, o fila 0 de cualquier caso de ∆0 , solo hay el único elemento del
conjunto {1} ,y para obtener el término correspondiente de igual número de fila en ∆ 𝑇, hay que
multiplicar dicha fila, por la unidad, que representa en cada caso el elemento de igual posición
relativa en la sucesión paralela 𝑆1 = {(
𝑖
0
)} = 1,1,1, … , 1
En la segunda fila o fila 1 de cualquier caso de ∆0, siempre tendremos los elementos del conjunto
{1,1}, y para obtener los términos correspondientes de igual número de fila en ∆ 𝑇, hay que
multiplicar dicha fila, por m, que representa en cada caso, el elemento de igual posición relativa en
la sucesión paralela 𝑆2 = {(
𝑖
1
)} = 1,2,3,4,5, … , 𝑛

8. En la tercera fila, o fila 2 de cualquier caso de ∆0, siempre tendremos los elementos del conjunto
{1,2,1}, y para obtener los términos correspondientes de igual número de fila en ∆ 𝑇 , hay que
multiplicar dicha fila, por el elemento de igual posición relativa en la sucesión paralela
𝑆3 = {(
𝑖
2
)} = 1,3,6,10, … ,
(𝑛 + 1)𝑛
2!
En la cuarta fila , o fila 3 de cualquier caso de ∆0, siempre tendremos los elementos del conjunto
{1,3,3,1}, , y para obtener los términos correspondientes de igual número de fila en ∆ 𝑇 , hay que
multiplicar dicha fila, por el elemento de igual posición relativa en la sucesión paralela
𝑆4 = {(
𝑖
3
)} = {1,4,10,20,35,56, … ,
(𝑛 + 2)(𝑛 + 1)𝑛
3!
}
Y así sucesivamente, para cada caso de m
Analíticamente, si a una fila genérica de ∆ 𝟎 , la denotamos como :
𝑭 𝒏
𝟎
= {(
𝒏
𝒊
)} = {(
𝒏
𝟎
) , (
𝒏
𝟏
) , (
𝒏
𝟐
) , … , (
𝒏
𝒏 − 𝟏
) , (
𝒏
𝒏
)}, la distribución de coeficientes trinomiales en la
fila n correspondiente de ∆ 𝑻 , vendrá dada por:
𝑭 𝒏
𝒎−𝒏
= (
𝒎
𝒏
) {(
𝒏
𝒊
)}, que podemos expresar trinomialmente como 𝑭 𝒏
𝒎−𝒏
= {(
𝒎
𝒏
𝒊
)} con 𝒊 =
𝟎, 𝟏, 𝟐, … , 𝒏, donde m, representa la potencia del trinomio, y n la fila considerada.
Podemos expresar cada una de estas multiplicaciones, indicadas en la obtención de los
coeficientes trinomiales, como los productos de los sucesivos coeficientes combinatorios
binomiales involucrados, y aplicar entonces la expresión definida para los coeficientes
multinomiales, al caso particular de los coeficientes trinomiales.
Así por ej. para el caso de m=0, y n=0, solo tendremos un valor:
𝐹0
0
= (
0
0
) {(
0
0
)} = (
0
0
) (
0
0
) = (
0
0
0
) = 1
Para m=1, y n= 0 y 1, tendremos 3 valores, uno en la fila 0, y dos en la fila 1
𝐹0
1
= (
1
0
) {(
0
0
)} = (
1
0
) (
0
0
) = (
1
0
0
) = 1
𝐹1
0
= (
1
1
) {(
1
0
) , (
1
1
)} = {(
1
1
) (
1
0
) , (
1
1
) (
1
1
)} {(
1
1
0
) , (
1
1
1
)} = 1,1
Para m=2, y n=0,1 y 2, tendremos 6 valores, uno en la fila 0, dos en la fila 1, y tres en la fila 3
𝐹0
2
= (
2
0
) {(
0
0
)} = (
2
0
) (
0
0
) = (
2
0
0
) = 1

9. 𝐹1
1
= (
2
1
) {(
1
0
) , (
1
1
)} = {(
2
1
) (
1
0
) , (
2
1
) (
1
1
)} = {(
2
1
0
) , (
2
1
1
)} = 2,2
𝐹2
0
= (
2
2
) {(
2
0
) , (
2
1
) , (
2
2
)} = {(
2
2
) (
2
0
) , (
2
2
) (
2
1
) , (
2
2
) (
2
2
)} = {(
2
2
0
) , (
2
2
1
) , (
2
2
2
)} = 1,2,1
Para m=3, y n= 0,1,2 y 3, tendremos 10 valores, 1 en la fila 0, dos en la fila 1, tres en la fila 2, y 4 en
la fila 3
𝐹0
3
= (
3
0
) {(
0
0
)} = (
3
0
) (
0
0
) = (
3
0
0
) = 1
𝐹1
2
= (
3
1
) {(
1
0
) , (
1
1
)} = {(
3
1
) (
1
0
) , (
3
1
) (
1
1
)} = {(
3
1
0
) , (
3
1
1
)}=3,3
𝐹2
1
= (
3
2
) {(
2
0
) , (
2
1
) , (
2
2
)} = {(
3
2
) (
2
0
) , (
3
2
) (
2
1
) , (
3
2
) (
2
2
)} = {(
3
2
0
) , (
3
2
1
) , (
3
2
2
)} = 3,6,3
𝐹3
0
= (
3
3
) {(
3
0
) , (
3
1
) , (
3
2
) , (
3
3
)} = {(
3
3
) (
3
0
) , (
3
3
)(
3
1
) , (
3
3
)(
3
2
) , (
3
3
)(
3
3
)} = {(
3
3
0
) , (
3
3
1
) , (
3
3
2
) , (
3
3
3
)} = 1,3,3,1
Y así sucesivamente, hasta el valor de m que consideremos necesario.
Notamos que en el caso de los coeficientes trinomiales, es la sucesión 𝑆3 = {(
𝑖
2
)} = 1,3,6,10, … ,
(𝑛+1)𝑛
2!
,
con i=3,4,…,(n+2) la que determina el número de elementos de cada fila.
Estos pocos valores obtenidos, ponen en evidencia la secuencia necesaria para su organización
en triángulos de coeficientes, como una analogía del triángulo de Pascal.
Para el caso de valores numéricos, podemos construir el cuadro siguiente:
TRIANGULO DE COEFICIENTES TRINOMIALES (NUMÉRICOS), desde m=0, hasta m=6
m Columnas ,como Filas de ∆ 𝑇 𝑆3
0 1 2 3 4 5 6
0 1 1
1 1 1 1 3
2 1 2 2 1 2 1 6
3 1 3 3 3 6 3 1 3 3 1 10
4 1 4 4 6 12 6 4 12 12 4 1 4 6 4 1 15
5 1 5 5 10 20 10 10 30 30 10 5 20 30 20 5 1 5 10 10 5 1 21
6 1 6 6 15 30 15 20 60 60 20 15 60 90 60 15 6 30 60 60 30 6 1 6 15 20 15 6 1 28

10. Notamos fácilmente que se pueden establecer unas reglas sencillas, para la obtención de los
elementos de cada columna del cuadro, en base a los valores recogidos en ∆ 𝟎:
Los elementos de la primera columna del cuadro anterior, (correspondiente a las filas 0 de ∆ 𝑇 ,
para cada caso de m), son todos iguales a la unidad. Se obtendrían multiplicando el único
elemento de la fila 0, de ∆ 𝟎 , es decir el conjunto {1} , sucesivamente por los elementos de la
sucesión paralela 𝑆1 = {(
𝑖
0
)} = 1,1,1, … , 1, productos que evidentemente siempre serán igual a 1.
Para obtener los elementos de la segunda columna (correspondientes a las filas 1 de ∆ 𝑇, para cada
caso de m), bastará multiplicar los dos elementos de la fila 1 de ∆ 𝟎 , es decir del conjunto {1,1} ,
sucesivamente, por los elementos de la sucesión paralela 𝑆2 = {(
𝑖
1
)} = 1,2,3, … , 𝑛,
Para obtener los elementos de la tercera columna (correspondientes a las filas 2 de ∆ 𝑇, para cada
caso de m ) bastará multiplicar los tres elementos de la fila 2 de ∆ 𝟎 , es decir del conjunto {1,2,1} ,
sucesivamente, por los elementos de la sucesión paralela 𝑆3 = {(
𝑖
2
)} = 1,3,6,10, … ,
(𝑛+1)𝑛
2!
Para obtener los elementos de la cuarta columna (correspondientes a las filas 3 de ∆ 𝑇, para cada
caso de m), bastará multiplicar los cuatro elementos de la fila 3 de ∆ 𝟎, es decir del conjunto
{1,3,3,1} , sucesivamente por los elementos de la sucesión paralela
𝑆4 = {(
𝑖
3
)} = {1,4,10,20,35,56, … ,
(𝑛 + 2)(𝑛 + 1)𝑛
3!
}
Y así sucesivamente.
La expresión 𝑭 𝒏
𝒎−𝒏
= (
𝒎
𝒏
) {(
𝒏
𝒊
)} = {(
𝒎
𝒏
𝒊
)}, con 𝒊 = 𝟎, 𝟏, … , 𝒏. para cada 𝒏 = 𝟎, 𝟏, … , 𝒎. sigue
siendo válida para calcular , u obtener los coeficientes trinomiales de cada fila de este triángulo
generalizado, pero tomando en cuenta que debemos aplicarla separadamente para cada n, como
valor de columna, considerada como fila de ∆ 𝑇,así p.ej.: para la fila 3 (m=3), tendríamos:
(
3
0
) {(
0
0
)}
= {(
3
0
0
)}
n=0. i=0
(
3
1
) {(
1
0
) , (
1
1
)}
= {(
3
1
0
) , (
3
1
1
)}
n=1. i=0,1
(
3
2
) {(
2
0
) , (
2
1
) , (
2
2
)}
= {(
3
2
0
) , (
3
2
1
) , (
3
2
2
)}
n=2 i=0,1,2
(
3
3
) {(
3
0
) , (
3
1
) , (
3
2
) , (
3
3
)}
= {(
3
3
0
) , (
3
3
1
) , (
3
3
2
) , (
3
3
3
)}
n=3 i=0,1,2,3
1 3 3 3 6 3 1 3 3 1
En general, para obtener los elementos de la columna 𝒏 de este triángulo de coeficientes
trinomiales, bastará multiplicar todos los elementos de la fila 𝒏 del triángulo de Pascal
(∆ 𝟎), sucesivamente, por los elementos de la sucesión paralela 𝑺 𝒏+𝟏 , con n=0,1,2,3,...

11. Del triángulo de valores combinatorios, hemos obtenido los siguientes coeficientes trinomiales:
para m=0, con una sola fila (fila0) : (
0
0
0
)
Para m=1, con dos filas (filas 0 y 1) : (
1
0
0
) , (
1
1
0
) , (
1
1
1
)
Para m=2, con tres filas ( filas 0,1,y 2 ) : (
2
0
0
) , (
2
1
0
) , (
2
1
1
) , (
2
2
0
) , (
2
2
1
) , (
2
2
2
)
Para m=3, con cuatro filas (filas 0,1,2,y 3) : (
3
0
0
) , (
3
1
0
) , (
3
1
1
) , (
3
2
0
) , (
3
2
1
) , (
3
2
2
) , (
3
3
0
) , (
3
3
1
) , (
3
3
2
) , (
3
3
3
)
Es inmediata la secuencia, que nos permite obtener los trinomiales de las filas sucesivas
TRIANGULO DE COEFICIENTES COMBINATORIOS TRINOMIALES (desde m=0, hasta m=4)
m Columnas, como Filas de ∆ 𝑇
0 1 2 3 4
0
(
0
0
0
)
1
(
1
0
0
) (
1
1
0
) (
1
1
1
)
2
(
2
0
0
) (
2
1
0
) (
2
1
1
) (
2
2
0
) (
2
2
1
) (
2
2
2
)
3
(
3
0
0
) (
3
1
0
) (
3
1
1
) (
3
2
0
) (
3
2
1
) (
3
2
2
) (
3
3
0
) (
3
3
1
) (
3
3
2
) (
3
3
3
)
4
(
4
0
0
) (
4
1
0
) (
4
1
1
) (
4
2
0
) (
4
2
1
) (
4
2
2
) (
4
3
0
) (
4
3
1
) (
4
3
2
) (
4
3
3
) (
4
4
0
) (
4
4
1
) (
4
4
2
) (
4
4
3
) (
4
4
4
)

12. COEFICIENTES TETRANOMIALES
De manera análoga a como cada una de las columnas del triangulo de coeficientes trinomiales se
genera a partir de los valores de cada una de las filas de ∆ 𝟎, el triángulo de coeficientes
Tetranomiales, se puede construir a partir del conjunto de los coeficientes de cada uno de los ∆ 𝑻,
correspondientes a cada caso de m, utilizando el mismo mecanismo de generación, por
intermedio de las sucesiones paralelas
Para obtener los coeficientes de la columna 0, del triangulo de coeficientes Tetranomiales,
bastará multiplicar el único elemento del triángulo de coeficientes trinomiales ∆ 𝑻, para m=0, es
decir del conjunto {1} , sucesivamente por los elementos de la sucesión 𝑆1 = {(
𝑖
0
)} = 1,1,1, … , 1
,
con i= 0,1,…,(n-1) , productos que evidentemente siempre serán igual a 1.
Para obtener los coeficientes de la columna 1, del triángulo de coeficientes Tetranomiales ,
bastará multiplicar todos los elementos del triángulo de coeficientes trinomiales ∆ 𝑻, para m=1,
es decir del conjunto {1,1,1} , sucesivamente, por los elementos de la sucesión: 𝑆2
= {(
𝑖
1
)} =
1,2,3, … , 𝑛,
con i=1,2,…,n
Para obtener los coeficientes de la columna 2, del triángulo de coeficientes Tetranomiales, bastará
multiplicar todos los elementos del triángulo de coeficientes trinomiales ∆ 𝑻,para m=2, es decir
del conjunto {1,2,2,1,2,1} , por los elementos de la sucesión 𝑆3 = {(
𝑖
2
)} = 1,3,6,10, … ,
(𝑛+1)𝑛
2!
,
con i=3,4,…,(n+2)
Para obtener los coeficientes de la columna 3, del triángulo de coeficientes Tetranomiales, bastará
multiplicar todos los elementos del triángulo de coeficientes trinomiales ∆ 𝑻, para m=3, es decir
del conjunto {1,3,3,3,6,3,1,3,3,1} , por los elementos de la sucesión :
𝑆4 = {(
𝑖
3
)} = {1,4,10,20,35,56, … ,
(𝑛+2)(𝑛+1)𝑛
3!
} , con i=3,4,…,(n+2)
Y así sucesivamente. Podemos concluir que para la obtención de los coeficientes de la columna 𝑛 ,
de este triángulo de coeficientes Tetranomiales, bastará multiplicar todos los elementos del
triángulo de coeficientes trinomiales ∆ 𝑻, para m=n , sucesivamente por los elementos de la
sucesión paralela 𝑆 𝑛+1, con 𝑛 = 0,1,2,3, …
Además , notamos que en el caso de los coeficientes Tetranomiales, es la sucesión
𝑆4 = {(
𝑖
3
)} = {1,4,10,20,35,56,… ,
(𝑛+2)(𝑛+1)𝑛
3!
}, la que determina el número total de elementos de cada
fila del triángulo
En base a estas reglas, hemos elaborado a continuación, el triángulo de coeficientes
Tetranomiales, correspondientes a los valores numéricos, desde m=0, hasta m=5.

13. TRIANGULO NUMERICO DE COEFICIENTES TETRANOMIALES (desde m=0, hasta m=5)
5 𝑆4
1 5 5 10 20 10 10 30 30 10 5 20 30 20 5 1 5 10 10 5 1 56
6 30 30 60 120 60 60 180 180 60 30 120 180 120 30 6 30 60 60 30 6
Como puede observarse, la primera fila de cada una de las columnas de la tabla corresponde al conjunto de los coeficientes trinomiales ∆ 𝑻,para
cada caso de m.
Para generar los coeficientes de las demás filas de cada columna, deberemos multiplicar los coeficientes de esa fila inicial sucesivamente, por los
elementos de la sucesión paralela correspondiente.
En general, para obtener los elementos de la columna 𝒏 de este triángulo de coeficientes tetranomiales, bastará multiplicar todos los
elementos del triángulo de coeficientes trinomiales ∆ 𝑻 , para m=n, sucesivamente, por los elementos de la sucesión paralela 𝑺 𝒏+𝟏 ,con
n=0,1,2,3,...
m
Columnas, como casos de ∆ 𝑻
𝑆4
0 1 2 3 4
0 1 1
1 1 1 1 1 4
2 1 2 2 2 1 2 2 1 2 1 10
3 1 3 3 3 3 6 6 3 6 3 1 3 3 3 6 3 1 3 3 1 20
4 1 4 4 4 6 12 12 6 12 6 4 12 12 12 24 12 4 12 12 4 1 4 4 6 12 6 4 12 12 4 1 4 6 4 1 35
5 1 5 5 5 10 20 20 10 20 10 10 30 30 30 60 30 10 30 30 10 5 20 20 30 60 30 20 60 60 20 5 20 30 20 5

14. Como en el caso del triángulo de coeficientes trinomiales, la construcción del triángulo de
coeficientes Tetranomiales no nos informa directamente sobre la distribución espacial de dichos
coeficientes. En el caso de los primeros, hemos determinado en el trabajo denominado “Prisma
Combinatorio” que los coeficientes trinomiales se agrupan en triángulos que hemos denominado
∆ 𝑻, y cuyo número de elementos siguen la secuencia correspondiente a la sucesión 𝑆3 . En el caso
de los coeficientes Tetranomiales, el número de sus coeficientes sigue la secuencia de la sucesión
𝑆4 , y en otro trabajo anterior, denominado “Distribución Tetraedrica de coeficientes
Tetranomiales” , hemos propuesto una distribución espacial en tetraedros regulares principales
(TP) , y tetraedros regulares secundarios (TS) , acompañados de tetraedros –punto o
singularidades , cuando m es múltiplo de 4. El desarrollo de este nuevo trabajo, ha permitido
confirmar tal distribución, y dar luces sobre la necesaria ubicación de estos TS, y singularidades, al
interior de los TP, ubicando siempre su vértice en el nivel 3 de los TP (utilizando la misma
contabilidad por nivel, que para las filas de ∆ 𝑻 ), y desarrollando sus niveles inferiores, hasta
colocar siempre su base a la altura del nivel 𝑛 − 1, del tetraedro principal del caso, para así
construir el que hemos denominado tetraedro suma, contenedor del total de los coeficientes del
caso de m considerado.
Analíticamente, hemos desarrollado una fórmula , que hemos ya utilizado para la determinación
de los coeficientes trinomiales: 𝑭 𝒏
𝒎−𝒏
= (
𝒎
𝒏
) {(
𝒏
𝒊
)} = {(
𝒎
𝒏
𝒊
)}, con i=0,1,...,n
Donde m representa la potencia del trinomio, y n representa la fila considerada de ∆ 𝑻,
correspondientes a las columnas del triángulo de coeficientes trinomiales.
Para la determinación de los coeficientes Tetranomiales, hemos también desarrollado una
expresión, que viene siendo una expansión al siguiente nivel, de la formula precedente:
𝑻 𝒏
𝒎
= (
𝒎
𝒏
) {(
𝒏
𝒊
𝒋
)} = {(
𝒎
𝒏
𝒊
𝒋
)}, con 𝒊 = 𝟎, 𝟏, 𝟐, … , 𝒏 y para cada 𝒊 , será 𝒋 = 𝟎, 𝟏, … , 𝒊
Donde m representa la potencia del tetranomio, y n representa el nivel correspondiente del
tetraedro suma que agrupa los coeficientes, desde n= cero en el vértice, hasta n=m en la base,
igual a ∆ 𝐓 para dicho caso de m, y que se corresponden con los valores de las columnas como
casos de ∆ 𝑻, en el triángulo de coeficientes Tetranomiales. Así, para obtener los coeficientes
Tetranomiales de la fila m=3, del triángulo correspondiente, deberemos aplicar la expresión
anterior, por cada nivel del tetraedro que los contiene, que equivalen a las columnas del mismo,
como casos de ∆ 𝑇
Nivel o columna: 0 , un único elemento
𝑻 𝟎
𝟑
= (
3
0
) {(
0
0
0
)} = {(
3
0
0
0
)} = {1}
i=0
j=0

15. Nivel o columna: 1, 3 elementos
𝑻 𝟏
𝟑
= (
3
1
) {(
1
0
0
) , (
1
1
0
) , (
1
1
1
)} = {(
3
1
0
0
) , (
3
1
1
0
) , (
3
1
1
1
)} = {3,3,3}
i=0 i=1
j=0 j=0 , 1
Nivel o columna : 2, 6 elementos
𝑻 𝟐
𝟑
= (
3
2
) {(
2
0
0
) , (
2
1
0
) , (
2
1
1
) , (
2
2
0
) , (
2
2
1
) , (
2
2
2
)} = {(
3
2
0
0
) , (
3
2
1
0
) , (
3
2
1
1
) , (
3
2
2
0
) , (
3
2
2
1
) , (
3
2
2
2
)} = {3,6,6,3,6,3}
I=0 i= 1 i=2
J=0 j= 0, 1 j=0 , 1 , 2
Nivel o columna: 3, 10 elementos
𝑻 𝟑
𝟑
= (
3
3
) {(
3
0
0
) , (
3
1
0
) , (
3
1
1
) , (
3
2
0
) , (
3
2
1
) , (
3
2
2
) , (
3
3
0
) , (
3
3
1
) , (
3
3
2
) , (
3
3
3
)} =
{(
3
3
0
0
) , (
3
3
1
0
) , (
3
3
1
1
) , (
3
3
2
0
) , (
3
3
2
1
) , (
3
3
2
2
) , (
3
3
3
0
) , (
3
3
3
1
) , (
3
3
3
2
) , (
3
3
3
3
)} = {1,3,3,3,6,3,1,3,3,1}
i=0 i=1 i=2 i=3
j=0 j=0, 1 j=0, 1, 2 j=0, 1, 2, 3
Utilizando esta misma expresión, podemos transformar cada uno de los valores ya recogidos en el
triángulo de coeficientes numéricos tetranomiales a su forma combinatoria, siendo la secuencia
resultante muy similar a la obtenida y utilizada para confeccionar la tabla de coeficientes
combinatorios trinomiales.
A continuación, con ciertas limitaciones por motivos de espacio en Word, hemos confeccionado la
tabla de coeficientes Tetranomiales combinatorios, desde m=0, hasta m=5.

16. TRIANGULO DE COEFICIENTES COMBINATORIOS TETRANOMIALES (desde m =0, hasta m= 5)
Notas:
Por razones de espacio, se han obviado los valores de m, que coinciden siempre con el primer valor constante en cada línea. Así mismo, no se
han colocado los valores dentro de los paréntesis ( ) del símbolo usual para coeficientes combinatorios.
Niveles del tetraedro o Columnas como casos de ∆ 𝑇
0 1 2 3 4 5
0
0
0
0
1
0
0
0
1
1
0
0
1
1
1
0
1
1
1
1
2
0
0
0
2
1
0
0
2
1
1
0
2
1
1
1
2
2
0
0
2
2
1
0
2
2
1
1
2
2
2
0
2
2
2
1
2
2
2
2
3
0
0
0
3
1
0
0
3
1
1
0
3
1
1
1
3
2
0
0
3
2
1
0
3
2
1
1
3
2
2
0
3
2
2
1
3
2
2
2
3
3
0
0
3
3
1
0
3
3
1
1
3
3
2
0
3
3
2
1
3
3
2
2
3
3
3
0
3
3
3
1
3
3
3
2
3
3
3
3
4
0
0
0
4
1
0
0
4
1
1
0
4
1
1
1
4
2
0
0
4
2
1
0
4
2
1
1
4
2
2
0
4
2
2
1
4
2
2
2
4
3
0
0
4
3
1
0
4
3
1
1
4
3
2
0
4
3
2
1
4
3
2
2
4
3
3
0
4
3
3
1
4
3
3
2
4
3
3
3
4
4
0
0
4
4
1
0
4
4
1
1
4
4
2
0
4
4
2
1
4
4
2
2
4
4
3
0
4
4
3
1
4
4
3
2
4
4
3
3
4
4
4
0
4
4
4
1
4
4
4
2
4
4
4
3
4
4
4
4
5
0
0
0
5
1
0
0
5
1
1
0
5
1
1
1
5
2
0
0
5
2
1
0
5
2
1
1
5
2
2
0
5
2
2
1
5
2
2
2
5
3
0
0
5
3
1
0
5
3
1
1
5
3
2
0
5
3
2
1
5
3
2
2
5
3
3
0
5
3
3
1
5
3
3
2
5
3
3
3
5
4
0
0
5
4
1
0
5
4
1
1
5
4
2
0
5
4
2
1
5
4
2
2
5
4
3
0
5
4
3
1
5
4
3
2
5
4
3
3
5
4
4
0
5
4
4
1
5
4
4
2
5
4
4
3
5
4
4
4
5
5
0
0
5
5
1
0
5
5
1
1
5
5
2
0
5
5
2
1
5
5
2
2
5
5
3
0
5
5
3
1
5
5
3
2
5
5
3
3
5
5
4
0
5
5
4
1
5
5
4
2
5
5
4
3
5
5
4
4
5
5
5
0
5
5
5
1
5
5
5
2
5
5
5
3
5
5
5
4
5
5
5
5

17. Es “evidente” que los resultados obtenidos hasta ahora en este trabajo, pueden ser extendidos
para cualquier potencia entera, y para cualquier polinomio de r términos. Las fórmulas y
secuencias a utilizar deberían resultar muy semejantes. El único inconveniente parece ser, el
determinar cómo se agrupan espacialmente dichos coeficientes, ya que para combinatorios
pentanomiales en adelante, estaríamos hablando de cuerpos de 4 o más dimensiones, de los
cuales, solo en algunos casos, podemos conocer sus proyecciones tridimensionales. Pero ello no
nos impide construir el triángulo correspondiente al caso general de coeficientes polinomiales, y
en este caso, resulta más práctico el triángulo de coeficientes combinatorios, ya que es inmediato
desarrollar las secuencias involucradas, en base a los casos anteriores que hemos determinado,
que luego se podrían fácilmente llevar a valores numéricos.
Para construir el triángulo de coeficientes numéricos pentanomiales por columnas, deberemos
partir en cada una de ellas del total de coeficientes del tetraedro que los contiene
correspondientes al mismo caso de m. Para ello bastará determinar dichos coeficientes en cada
nivel del tetraedro suma. Así por ejemplo el total de coeficientes de la fila 3 del triangulo de
coeficientes Tetranomiales, constituyen los coeficientes de partida de la columna 3, del triangulo
de coeficientes pentanomiales.
COEFICIENTES PENTANOMIALES
También hemos expandido y comprobado la expresión utilizada para el cálculo, al caso de los
coeficientes pentanomiales:
𝑸 𝒏
𝒎
= (
𝒎
𝒏
) {(
𝒏
𝒊
𝒋
𝒌
)} =
{(
𝒎
𝒏
𝒊
𝒋
𝒌 )}
, donde m representa la potencia del pentanomio o fila del
triángulo de coeficientes, y n representa el nivel correspondiente del cuerpo 4D que los
contiene, desde n=0 en el “vértice”, hasta n=m en la base o tetraedro suma de coeficientes
Tetranomiales para dicho caso de m, y donde n se corresponde con los valores de columna como
casos de tetraedro suma, en el triángulo de coeficientes. La secuencia de los elementos de los
tetranomios , y de los pentanomios involucrados, vendrá dada por:
𝑖 = 0,1,2, … , 𝑛
Para i=0
j=0 una sola vez, y k=0 una sola vez
Para i=1
j= 1vez 0 y k=0
j= 2 veces 1 k=0,1
Para i=2
j= 1vez 0 k=0
j= 2veces 1 k=0,1
j= 3veces 2 k=0,1,2

18. Para i= 3
j= 1vez 0 k=0
j= 2veces 1 k=0,1
j= 3veces 2 k=0,1,2
j= 4veces 3 k=0,1,2,3
Así sucesivamente.
Comprobemos entonces lo afirmado anteriormente, calculando los coeficientes correspondientes
a la fila 𝑚 = 3 , del triángulo de coeficientes pentanomiales, mediante la expresión ya obtenida.
Columna 0 1elemento
𝑸 𝟎
𝟑
= (
3
0
) {(
0
0
0
0
)} =
{(
3
0
0
0
0)}
= {1}
Columna 1 4 elementos
𝑸 𝟏
𝟑
= (
3
1
) {(
1
0
0
0
) , (
1
1
0
0
) , (
1
1
1
0
) , (
1
1
1
1
)} =
{(
3
1
0
0
0)
,
(
3
1
1
0
0)
,
(
3
1
1
1
0)
,
(
3
1
1
1
1)}
={3,3,3,3}
Columna 2 10 elementos
𝑸 𝟐
𝟑
= (
3
2
) {(
2
0
0
0
) , (
2
1
0
0
) , (
2
1
1
0
) , (
2
1
1
1
) , (
2
2
0
0
) , (
2
2
1
0
) , (
2
2
1
1
) , (
2
2
2
0
) , (
2
2
2
1
) , (
2
2
2
2
)} =
{(
3
2
0
0
0)
,
(
3
2
1
0
0)
,
(
3
2
1
1
0)
,
(
3
2
1
1
1)
,
(
3
2
2
0
0)
,
(
3
2
2
1
0)
,
(
3
2
2
1
1)
,
(
3
2
2
2
0)
,
(
3
2
2
2
1)
,
(
3
2
2
2
2)}
= {3,6,6,6,3,6,6,3,6,3}
Columna 3 20 elementos
𝑸 𝟑
𝟑
=
(
3
3
) {(
3
0
0
0
) , (
3
1
0
0
) , (
3
1
1
0
) , (
3
1
1
1
) , (
3
2
0
0
) , (
3
2
1
0
) , (
3
2
1
1
) , (
3
2
2
0
) , (
3
2
2
1
) , (
3
2
2
2
) , (
3
3
0
0
) , (
3
3
1
0
) , (
3
3
1
1
) , (
3
3
2
0
) , (
3
3
2
1
) , (
3
3
2
2
) , (
3
3
3
0
) , (
3
3
3
1
) , (
3
3
3
2
) , (
3
3
3
3
)} =
{(
3
3
0
0
0)
,
(
3
3
1
0
0)
,
(
3
3
1
1
0)
,
(
3
3
1
1
1)
,
(
3
3
2
0
0)
,
(
3
3
2
1
0)
,
(
3
3
2
1
1)
,
(
3
3
2
2
0)
,
(
3
3
2
2
1)
,
(
3
3
2
2
2)
,
(
3
3
3
0
0)
,
(
3
3
3
1
0)
,
(
3
3
3
1
1)
,
(
3
3
3
2
0)
,
(
3
3
3
2
1)
,
(
3
3
3
2
2)
,
(
3
3
3
3
0)
,
(
3
3
3
3
1)
,
(
3
3
3
3
2)
,
(
3
3
3
3
3)}
=
{1,3,3,3,3,6,6,3,6,3,1,3,3,3,6,3,1,3,3,1}
Estos últimos 20 valores, como ya hemos señalado, corresponden al total de coeficientes de la fila
3 del triángulo de coeficientes Tetranomiales y a su vez son los valores iniciales de la columna 3,
del triángulo de coeficientes pentanomiales .

19. TRIÁNGULO DE COEFICIENTES PENTANOMIALES (NUMÉRICOS), desde m=0, hasta m=6
m
Columnas como casos de T.Suma 𝑁°𝐸𝑙𝑒𝑚
𝑝/𝑓. 𝑆 50 1 2 3
0 1 1
1 1 1 1 1 1 5
2 1 2 2 2 2 1 2 2 2 1 2 2 1 2 1 15
3 1 3 3 3 3 3 6 6 6 3 6 6 3 6 3 1 3 3 3 3 6 6 3 6 3 1 3 3 3 6 3 1 3 3 1 35
4 1 4 4 4 4 6 12 12 12 6 12 12 6 12 6 4 12 12 12 12 24 24 12 24 12 4 12 12 12 24 12 4 12 12 4
5 1 5 5 5 5 10 20 20 20 10 20 20 10 20 10 10 30 30 30 30 60 60 30 60 30 10 30 30 30 60 30 10 30 30 10
6 1 6 6 6 6 15 30 30 30 15 30 30 15 30 15 20 60 60 60 60 120 120 60 120 60 20 60 60 60 120 60 20 60 60 20
4 𝑆5
70
1 4 4 4 6 12 12 6 12 6 4 12 12 12 24 12 4 12 12 4 1 4 4 6 12 6 4 12 12 4 1 4 6 4 1
5 20 20 20 30 60 60 30 60 30 20 60 60 60 120 60 20 60 60 20 5 20 20 30 60 30 20 60 60 20 5 20 30 20 5
15 60 60 60 90 180 180 90 180 90 60 180 180 180 360 180 60 180 180 60 15 60 60 90 180 90 60 180 180 60 15 60 90 60 15
5
1 5 5 5 10 20 20 10 20 10 10 30 30 30 60 30 10 30 30 10 5 20 20 30 60 30 20 60 60 20 5 20 30 20 5
6 30 30 30 60 120 120 60 120 60 60 180 180 180 360 180 60 180 180 60 30 120 120 180 360 180 120 360 360 120 30 120 180 120 30
5 𝑆5
1261 5 5 10 20 10 10 30 30 10 5 20 30 20 5 1 5 10 10 5 1
6 30 30 60 120 60 60 180 180 60 30 120 180 120 30 6 30 60 60 30 6
6
1 6 6 6 15 30 30 15 30 15 20 60 60 60 120 60 20 60 60 20 15 60 60 90 180 90 60 180 180 60 15 60 90 60 15

20. 6
6 30 30 60 120 60 60 180 180 60 30 120 180 120 30 6 30 60 60 30 6 1 6 6 15 30 15 20 60 60 20 15 60 90 60
6 𝑆5
15 6 30 60 60 30 6 1 6 15 20 15 6 1 2 210
 Esta cuarta tabla o triángulo, contiene todos los coeficientes del desarrollo de (𝑥1 + 𝑥2 + 𝑥3 + 𝑥4 + 𝑥5) 𝑚
, los cuales se distribuyen como
un todo en el volumen de un cuerpo de 4 dimensiones para cada potencia m del pentanomio, y aunque no podemos visualizar dichos
cuerpos o representarlos fácilmente en 3D, queda claro que cada una de sus secciones, trazadas por cada uno de sus niveles ( de m=0
,hasta n=m), corresponde a un tetraedro suma , con características análogas a las ya determinadas para tales cuerpos geométricos.
 Los coeficientes de este caso, que se distribuyen en dicho cuerpo 4D, responden a la expresión:
𝑸 𝒏
𝒎
=
{(
𝒎
𝒏
𝒊
𝒋
𝒌 )}
, donde m representa la potencia del pentanomio o fila del triángulo de coeficientes, y n representa el nivel
correspondiente del cuerpo 4D que los contiene o H.T.S. , desde n=0 en el “vértice”, hasta n=m en la base o tetraedro suma de
coeficientes Tetranomiales para dicho caso de m.
La secuencia a seguir para la obtención de los coeficiente pentanomiales , responde a:
𝒎 = 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕𝒆
𝒏 = 𝟎, 𝟏, … , 𝒎
𝒊 = 𝟎, 𝟏, … , 𝒏
𝒋 = 𝟎, 𝟏, … , 𝒊
𝒌 = 𝟎, 𝟏, … , 𝒌
 Los coeficientes de una fila son todos los contenidos en el cuerpo 4D para el caso de m.
 Los coeficientes iniciales de cada columna de la tabla o triángulo,se corresponden con el total de los coeficientes del T.Suma para m=n.
 Para obtener los valores de cada columna en la tabla, deberemos multiplicar cada uno de los valores iniciales de la columna n
(correspondientes al T.Suma para m=n), sucesivamente por los elementos de la sucesión paralela 𝑆 𝑛+1

21. Podemos inferir que la expresión, ya utilizada para el cálculo de los coeficientes trinomiales,
Tetranomiales y pentanomiales, puede expandirse y generalizarse para coeficientes polinomiales
de r elementos, aplicable a un polinomio elevado a cualquier potencia m entera positiva,
mediante:
𝑷 𝒏
𝒎
= (
𝒎
𝒏
)
{(
𝒏
𝒊
𝒋
𝒌
⋮
𝒑
𝒒)}
=
{(
𝒎
𝒏
𝒊
𝒋
𝒌
⋮
𝒑
𝒒 )}
, siendo m la potencia del polinomio y n el nivel considerado.
Con una secuencia para cada uno de los r términos involucrados m, n,i, j,k...p,q muy similar a la
ya utilizada en el caso de los coeficientes pentanomiales, que podemos sintetizar simbólicamente
como: 𝒎 = 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕𝒆
𝒏 = 𝟎, 𝟏, … , 𝒎
𝒊 = 𝟎, 𝟏, … , 𝒏
𝒋 = 𝟎, 𝟏, … , 𝒊
𝒌 = 𝟎, 𝟏, … , 𝒋
⋮
𝒑 = 𝟎, 𝟏, … , 𝒐
𝒒 = 𝟎. 𝟏, … , 𝒑
El desarrollo de estas secuencias para el caso general, son relativamente fáciles de deducir del
triángulo de coeficientes combinatorios polinomiales que presentamos a continuación
Este triángulo general de combinatorios polinomiales, será aplicable para un polinomio tal como:
(𝒙 𝟏 + 𝒙 𝟐 + 𝒙 𝟑 + ⋯ + 𝒙 𝒓) 𝒎
Y el número total de términos en cada fila, responderá sucesivamente, a los elementos de la sucesión
paralela: 𝑺 𝒓 = {𝟏,
𝒓
𝟏!
,
(𝒓+𝟏)𝒓
𝟐!
,
(𝒓+𝟐)(𝒓+𝟏)𝒓
𝟑!
, … ,
[𝒏+(𝒓−𝟐)][𝒏+(𝒓−𝟑)]…𝒏
(𝒓−𝟏)!
}
m=0 , un único elemento
(
0
0
0
0
0..
.
0
0)
m=1,
𝑟
1!
elementos
(
1
0
0
0
0
0
0
0
0
0) (
1
1
0
0
0
0
0
0
0
0)
…
(
1
1
1
1
1
..
.
1
0) (
1
1
1
1
1
1
1
1
1
1)

22. m=2,
(𝑟+1)
2!
elementos
(
2
0
0
0
0...
0
0
) (
2
1
0
0
0...
0
0
)
…
(
2
1
1
1
1...
1
0
) (
2
1
1
1
1...
1
1
) (
2
2
0
0
0...
0
0
) (
2
2
1
0
0...
0
0
)
…
(
2
2
1
1
1...
1
1
) (
2
2
2
0
0...
0
0
) (
2
2
2
1
0...
0
0
)
…
(
2
2
2
1
1...
1
1
)(
2
2
2
2
0...
0
0
)
…
(
2
2
2
2
2...
2
2
)
m=3,
(𝑟+2)(𝑟+1)𝑟
3!
elementos
(
3
0
0
0
0...
0
0
) (
3
1
0
0
0...
0
0
)
…
(
3
1
1
1
1...
1
1
) (
3
2
0
0
0...
0
0
) (
3
2
1
0
0...
0
0
)
…
(
3
2
1
1
1...
1
1
)(
3
2
2
0
0...
0
0
)
…
(
3
2
2
2
2...
2
2
) (
3
3
0
0
0...
0
0
) (
3
3
1
0
0...
0
0
)
…
(
3
3
1
1
1...
1
1
) (
3
3
2
0
0...
0
0
) (
3
3
2
1
0...
0
0
) (
3
3
2
1
1...
0
0
)
…
(
3
3
2
1
1...
1
1
) (
3
3
2
2
0...
0
0
)
…
(
3
3
2
2
2...
2
2
) (
3
3
3
0
0...
0
0
)
…
(
3
3
3
3
3...
3
3
)
.....................................................................................................................................................................................
m=n,
[𝑛−(𝑟−2)][𝑛−(𝑟−3)]…𝑛
(𝑟−1)!
elementos
(
𝑛
0
0
0
0...
0
0
) (
𝑛
1
0
0
0...
0
0
)
…
(
𝑛
1
1
1
1...
1
1
) (
𝑛
2
0
0
0...
0
0
) (
𝑛
2
1
0
0...
0
0
)
…
(
𝑛
2
1
1
1...
1
1
) (
𝑛
2
2
0
0...
0
0
)
…
(
𝑛
2
2
2
2...
2
2
) (
𝑛
3
0
0
0...
0
0
) (
𝑛
3
1
0
0...
0
0
)
…
(
𝑛
𝑛 − 1
0
0
0...
0
0
) (
3
𝑛 − 1
1
0
0...
0
0
)
…
(
𝑛
𝑛 − 1
1
1
1...
1
1
)
…
(
𝑛
𝑛 − 1
𝑛 − 1
𝑛 − 1
𝑛 − 1...
𝑛 − 1
𝑛 − 1
) (
𝑛
𝑛
0
0
0...
0
0
) (
𝑛
𝑛
1
0
0...
0
0
)
…
(
𝑛
𝑛
𝑛 − 1
𝑛 − 1
𝑛 − 1...
𝑛 − 1
𝑛 − 1
) (
𝑛
𝑛
𝑛
0
0...
0
0
)
…
(
𝑛
𝑛
𝑛
𝑛
𝑛...
𝑛
𝑛
)

23. Notas finales:
Así como el número total de elementos en una fila para cualquier caso de m, responde
sucesivamente a los términos de la sucesión paralela 𝑺 𝒓 , el número de elementos por columna
responde a la secuencia de la sucesión paralela 𝑺 𝒓−𝟏
Si se multiplican los coeficientes de las filas 0,1,...,m, de uno cualquiera de estos triángulos de
coeficientes para un determinado valor de r, por los coeficientes respectivos (de igual posición
relativa) , de la fila m de ∆ 𝟎, se obtienen los coeficientes de la fila m, del triángulo de
coeficientes correspondientes al caso siguiente ( r+1).
Con este caso general, creemos que por ahora, hemos agotado el tema de los coeficientes
multinomiales y su aplicación a la generalización del triángulo de Pascal.
Enrique R. Acosta R. 2016