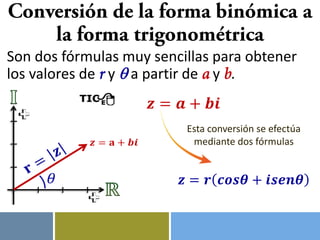
El documento explica cómo convertir números complejos de la forma binómica (a + bi) a la forma trigonométrica (r(cosθ + isenθ)) usando dos fórmulas. También describe cómo aplicar el Teorema de De Moivre para elevar números complejos a potencias o extraer raíces usando la forma trigonométrica.

1. G. Edgar Mata Ortiz

2. Los números complejos generalmente se
representan en forma binómica:

3. La forma binómica del número complejo
es útil para efectuar las operaciones
aritméticas básicas; suma, resta
multiplicación y división.

4. Para elevar un número complejo a una
potencia, o extraer raíces cuadradas, se
emplea el Teorema de Möivre, el cuál requiere
que el número esté expresado en forma
trigonométrica.

5. Para comprender mejor
el proceso que nos
permite convertir la
expresión de un número
complejo de la forma
binómica a la forma
trigonométrica debemos
recordar el plano
complejo.

6. Son dos fórmulas muy sencillas para obtener
los valores de r y q a partir de a y b.
𝒛 = 𝒂 + 𝒃𝒊
Originalmente el
número está
expresado en forma
binómica.

7. Son dos fórmulas muy sencillas para obtener
los valores de r y q a partir de a y b.
𝒛 = 𝒂 + 𝒃𝒊
Originalmente el número
está expresado en forma
binómica.
Debe convertirse a la
forma trigonométrica

8. Son dos fórmulas muy sencillas para obtener
los valores de r y q a partir de a y b.
𝒛 = 𝒂 + 𝒃𝒊
Originalmente el número está
expresado en forma binómica.
Debe convertirse a la
forma trigonométrica
𝒛 = 𝒓 𝒄𝒐𝒔𝜽 + 𝒊𝒔𝒆𝒏𝜽

9. Son dos fórmulas muy sencillas para obtener
los valores de r y q a partir de a y b.
𝒛 = 𝒂 + 𝒃𝒊
𝒛 = 𝒓 𝒄𝒐𝒔𝜽 + 𝒊𝒔𝒆𝒏𝜽
Esta conversión se efectúa
mediante dos fórmulas

10. Son dos fórmulas muy sencillas para obtener
los valores de r y q a partir de a y b.
𝒓 = 𝒂2 + 𝒃2
𝒛 = 𝒂 + 𝒃𝒊 𝒛 = 𝒓 𝒄𝒐𝒔𝜽 + 𝒊𝒔𝒆𝒏𝜽
𝜽 = 𝒂𝒓𝒄𝒕𝒂𝒏
𝒃
𝒂

11. Expresar el número:
En forma trigonométrica
𝒓 = 𝒂2 + 𝒃2
𝜽 = 𝒂𝒓𝒄𝒕𝒂𝒏
𝟒𝟓
𝟐𝟖
𝒛 = 𝟐𝟖 + 𝟒𝟓𝒊
𝒓 = 𝟐𝟖2 + 𝟒𝟓2

12. Expresar el número:
En forma trigonométrica
𝜽 = 𝒂𝒓𝒄𝒕𝒂𝒏
𝟒𝟓
𝟐𝟖
𝒛 = 𝟐𝟖 + 𝟒𝟓𝒊
𝒓 = 𝟐𝟖2 + 𝟒𝟓2
𝒓 = 𝟕𝟖𝟒 + 𝟐𝟎𝟐𝟓
𝒓 = 𝟕𝟖𝟒 + 𝟐𝟎𝟐𝟓
𝒓 = 𝟐𝟖𝟎𝟗
𝒓 = 53
𝜽 = 𝒂𝒓𝒄𝒕𝒂𝒏𝟏. 𝟔𝟎𝟕
𝜽 = 𝟏. 𝟎𝟏𝟒

13. 𝒛 = 𝟐𝟖 + 𝟒𝟓𝒊
𝒓 = 53 𝜽 = 𝟏. 𝟎𝟏𝟒
𝒛 = 𝟓𝟑 𝒄𝒐𝒔(𝟏. 𝟎𝟏𝟒) + 𝒊𝒔𝒆𝒏(𝟏. 𝟎𝟏𝟒)

14. 𝒛 = 𝟐𝟖 + 𝟒𝟓𝒊
𝒓 = 53 𝜽 = 𝟏. 𝟎𝟏𝟒
𝒛 = 𝟓𝟑 𝒄𝒐𝒔(𝟏. 𝟎𝟏𝟒) + 𝒊𝒔𝒆𝒏(𝟏. 𝟎𝟏𝟒)
Forma binómica
Forma trigonométrica

16. Para elevar un
número complejo a
una potencia
entera se aplica el
Teorema de:
De Möivre

17. Una vez convertido el número a+bi a la forma
trigonométrica, podemos aplicar el Teorema:

18. Ejemplo: Elevar el número z =28+45i al cuadrado:

19. Ejemplo: Elevar el número z =28+45i al cuadrado:

20. Ejemplo: Elevar el número z =28+45i, al cuadrado:

21. Puede parecer muy complicado convertir primero
a la forma polar y luego aplicar el teorema de De
Möivre, sin embargo, este método es muestra su
utilidad cuando se eleva a potencias muy grandes.
Por ejemplo:
Eleva z =1–i, a la décima potencia.

23. Para obtener la raíz
cuadrada, cúbica o
enésima, también
se aplica el
Teorema de:
De Möivre

24. Una vez convertido el número a+bi a la forma
trigonométrica, podemos aplicar el teorema,
escribiendo la raíz como una potencia
fraccionaria.

25. Una vez convertido el número a+bi a la forma
trigonométrica, podemos aplicar el teorema,
escribiendo la raíz como una potencia fraccionaria y,
tomando en cuenta que las funciones
trigonométricas son periódicas, realizar un ajuste en
a fórmula.

26. El ajuste en la fórmula consiste en agregar la
periodicidad como se muestra:

27. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 1. Convertir a la forma trigonométrica.

28. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 1. Convertir a la forma trigonométrica.

29. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 1. Convertir a la forma trigonométrica.

30. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 1. Convertir a la forma trigonométrica.

31. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 2. Sustituir en la fórmula de De Möivre.

32. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 2. Sustituir en la fórmula de De Möivre.

33. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 2. Sustituir en la fórmula de De Möivre.

34. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 2. Sustituir en la fórmula de De Möivre.
La primera de las tres soluciones es:
𝐤 = 𝟎

35. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 2. Sustituir en la fórmula de De Möivre.

36. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 2. Sustituir en la fórmula de De Möivre.
La segunda de las tres soluciones es:
𝐤 = 𝟏

37. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 2. Sustituir en la fórmula de De Möivre.

38. Ejemplo: Obtener la raíz cúbica de: 2 + i
Paso 2. Sustituir en la fórmula de De Möivre.
La tercera de las tres soluciones es:
𝐤 = 𝟐

39. Ejemplo: Obtener la raíz cúbica de: 2 + i
Las tres soluciones en forma trigonométrica son:

40. Ejemplo: Obtener la raíz cúbica de: 2 + i
Las tres soluciones en forma binómica son:

41. Fuentes de información en línea:
http://licmata-math.blogspot.mx/
http://www.scoop.it/t/mathematics-learning
https://www.facebook.com/licemata
https://www.linkedin.com/in/licmata
Twitter @licemata