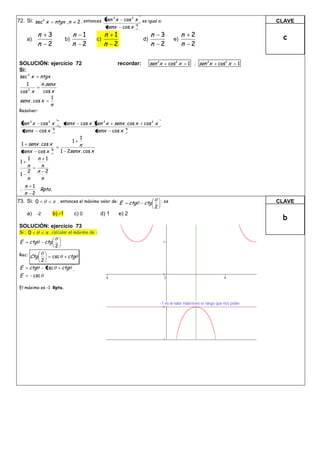
El documento contiene la solución de varios ejercicios de trigonometría. El ejercicio 69 involucra ángulos coterminales y hallar el menor de ellos. El ejercicio 71 calcula K sabiendo valores de tangentes. El ejercicio 72 relaciona funciones seno, coseno y tangente.

1. Segundo Examen Sumativo Cepuns 2012 II – Trigonometría
69. Los ángulos y son coterminales y se encuentran en relación de 5 es a 4 respectivamente. CLAVE
Hallar el menor de ellos sabiendo que el mayor es menos que 3700º pero mayor que 2360º.
a) 1800º b) 2560º c) 2880º d) 3300º e) 3600º
SOLUCIÓN: ejercicio 69
c
360º.k
;K=2
5a 4a 360k
a 360º.k
Por el dato del ángulo mayor
2360º 5a 3700º
472º a 740º
a 720º
Calculando el menor ángulo 4a 4(720º )
4a 2880º
70. Sabiendo que: Csc a 2
1 2(ctg 2b Csc 2b ) , calcular Y tgb CLAVE
tga
a) 2 b) 1 c) 3 d) -2 e) -1
a
SOLUCIÓN: ejercicio 69
Csc a 2
1 2(2ctg b 2
1)
Csc a 2
1 4ctg b2
Ctg a 2
4Ctg 2b
tg 2b
4
tg 2a
tgb
2
tga
71. Si: tg( - ) = 2 y tg( ) = 3, calcular: K 7sen 2 cos 2 CLAVE
a) 1 b) 0 c) -1 d) 2 e) -2
SOLUCIÓN: ejercicio 71 b
Reemplazar:
A
B
Tenemos:
tgA tgB
tg 2
1 tgA.tgB
3 2 1
tg 2
1 2.3 7
Ósea queda el triangulo siguiente:
Calcular:
K 7sen 2 cos 2
1 7
K 7 0
5 2 5 2
Rpta. 0

2. 2 , entonces sen x cos 3 x es igual a:
3
72. Si: sec2 x ntgx , n CLAVE
senx cos x 3
n 3 n 1 n 1 n 3 n 2 c
a) b) c) d) e)
n 2 n 2 n 2 n 2 n 2
SOLUCIÓN: ejercicio 72 recordar: sen 2x cos2 x 1 ; sen 2x cos2 x 1
Si:
sec 2 x ntgx
1 n .senx
cos x2
cos x
1
senx . cos x
n
Resolver:
sen 3 x cos 3 x senx cos x sen 2 x senx . cos x cos 2 x
senx cos x 3 senx cos x 3
1
1
1 senx . cos x n
senx cos x 2 1 2senx . cos x
1 n 1
1
n n
2 n 2
1
n n
n 1
Rpta .
n 2
73. Si: 0 , entonces el máximo valor de: E ctg ctg ; es CLAVE
2
a) -2 b) -1 c) 0 d) 1 e) 2
b
SOLUCIÓN: ejercicio 73
Si : 0 , calcular el máximo de :
E ctg ctg
2
Rec: Ctg csc ctg
2
E ctg csc ctg
E csc
El máximo es -1 Rpta.

3. +cos x = a ; entonces P = cos 3x – sen 3x , es iguial a:
74. si: senx CLAVE
a) 2a 3a b) a 3a c) 3a 5 2a d) 3a 2a a2 2a
2 2 3
e)
d
SOLUCIÓN: ejercicio 74
senx cos x 2
a2
Si: senx +cos x = a
1 2senx . cos x a2
a2 1
senx . cos x
2
Calcular : cos 3x – sen 3x
Sabemos que:
sen 3x 3senx 4sen 3 x
cos 3x 4 cos 3 x 3 cos x
x 3 y 3 x y x 2 x .y y2
Reemplazando:
4Cos 3 x 3 cos x 3senx 4sen 3 x
4 cos 3 x sen 3 x 3 senx cos x
4 senx cos x sen x 2
cos x
2
senx . cos x 3 senx cos x
reemplazan do :
a2 1 2 a2 1
4a 1 3a 4a 3a
2 2
6a 2a 3 3a 3a 2a 3
Rpta 3a 2a 3