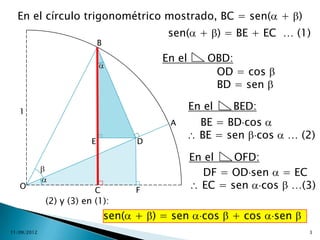
Este documento describe funciones trigonométricas para ángulos compuestos, ángulos dobles y ángulos mitad. Explica cómo calcular sen, cos y tan para la suma y diferencia de ángulos, y cómo estas funciones se pueden expresar en términos de los ángulos originales. También muestra fórmulas para sen, cos y tan de ángulos dobles y cómo calcular estas funciones para ángulos mitad. Incluye ejemplos resueltos.

1. Funciones Trigonométricas de ángulos compuestos,
ángulo doble y ángulo mitad.
11/09/2012 1

2. Funciones Trigonométricas de Ángulos Compuestos
Un ángulo compuesto es aquel formado por la suma o
diferencia de dos o mas ángulos simples ( , , ..)
Determinaremos las F.T. de ángulos de la forma:
+ y
-
En términos de las F.T. de y .
Para ello usaremos el círculo trigonométrico y la
resolución de triángulos rectángulos vista
anteriormente.
11/09/2012 2

3. En el círculo trigonométrico mostrado, BC = sen( + )
sen( + ) = BE + EC … (1)
B
En el OBD:
OD = cos
BD = sen
1
En el BED:
A BE = BD cos
BE = sen cos … (2)
E D
En el OFD:
DF = OD sen = EC
O
C F
EC = sen cos …(3)
(2) y (3) en (1):
sen( + ) = sen cos + cos sen
11/09/2012 3

4. Ejercicio Resuelto 1:
Calcular Cos 75º
Cos75º Cos(30º 45º )
Cos75º Cos30º.Cos 45º Sen30º.Sen45º
3 2 1 2
Cos75º . .
2 2 2 2
6 2
Cos75º
4 4
6 2
Cos75º
4
11/09/2012 4

5. Tarea:
Determine el valor exacto de las expresiones:
a) sen 75º
b) sen (7π/12)
11/09/2012 5

6. Análogamente se obtiene:
cos( + ) = cos cos - sen sen
Se puede demostrar:
tan α tanβ
tan(α β)
1 tanα tanβ
Para la diferencia se tiene:
sen( - ) = sen cos - cos sen
cos( - ) = cos cos + sen sen
y:
tan α tanβ
tan(α β)
1 tanα tanβ
11/09/2012 6

7. Ejercicio Resuelto 2:
Simplificar: Sen(60º x) Sen(60º x)
L
Cosx
Sen(60º x) Sen(60º x)
L
Cosx
Sen60º.Cosx Senx.Cos60º Sen60º.Cosx Senx.Cos60º
L
Cosx
2( Sen60º.Cosx )
L
Cosx
2 3
L
2
L 3
11/09/2012 7

8. Tarea:
Calcule el valor exacto de:
sen 20º cos 40º + cos 20º sen 40º
11/09/2012 8

9. Tarea:
Del gráfico mostrado calcular Tan(x)
Rpta: 9/23
11/09/2012 9

10. Funciones Trigonométricas del Ángulo Doble
Si en las diapositivas anteriores reemplazamos por
se obtendrá:
sen 2α 2sen α cos α ........ (1)
cos 2α cos 2α sen2α ...... (2a)
1 2sen2α ............ (2b)
2cos 2α 1............ (2c)
2tan α
tan 2α 2
.............. (3)
1 tan α
11/09/2012 10

11. Ejercicio Resuelto 3:
Si , Sen 4 calculemos Sen2 , Cos 2 , Tg 2
5
Sen2 2 Sen .Cos
4 3 24
Sen2 2. .
5 5 25
Cos 2 Cos 2 Sen 2
9 16 7
Cos 2
25 25 25
24
25 24
Tg 2
7 7
25
11/09/2012 11

12. Tarea:
Si cos x = -2/3 y x está en el cuadrante II, determine
sen 2x y cos 2x.
11/09/2012 12

13. Funciones Trigonométricas del Ángulo Mitad
Si en las expresiones (2b) y (2c) del ángulo doble,
reemplazamos 2α por x, entonces α = x , por lo que
2
obtendremos:
cos x 1 2sen2 ( x )
2
1 cos x
Despejando queda: sen( x )
2 2
1 cos x
También: cos( x )
2 2
dividiendo: 1 cos x
tan( x )
2 1 cos x
1 cos x sen x
racionalizando: tan( x )
2 sen x 1 cos x
11/09/2012 13

14. Ejercicio Resuelto 3:
Si: 5
180º 270º ; Sen ,
3 5
calcular Cos , Sec , Tg , Ctg
2 2 2 2
1 cos 1 cos sen 32
2
a2
cos( ) tan( ) 5
2 2 2 sen 1 cos 9 5 a2
sen
2 tan( ) 4 a2
1 2 1 cos
2 a
cos( ) 3
5
2 2 -
tan( ) 3
5 2 2
1
cos( ) 3 3
2 2 5
-
1 tan( ) 3
2 1
cos( ) 5 3
2 6
tan( ) 5
1 2
Sec( )
2 5 1
Ctg ( )
6 2 5
11/09/2012 14

15. Tarea:
Determine tan(u/2) si sen u = 2/5 y u está en el
cuadrante II.
RPTA : tan(u) 5 21
2 2
11/09/2012 15

16. 11/09/2012 16