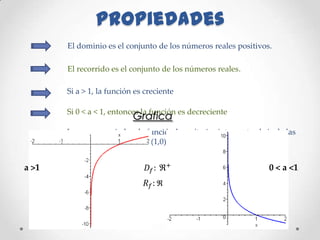
Este documento resume las propiedades y aplicaciones de las funciones logarítmicas. Explica que la logaritmación es el proceso de encontrar el exponente de una potencia y define la función logarítmica como la inversa de la función exponencial. Además, presenta ejemplos de cómo se usan los logaritmos para representar medidas que abarcan un amplio rango de valores y cómo la escala de Richter emplea logaritmos para comparar la intensidad de los terremotos.

1. Álgebra de
Funciones
Integrante:  Juan Esteban Villablanca
Profesor:  Luis Schorwer

2. Logaritmación
, el proceso de encontrar el exponente de
una potencia se llama LOGARITMACION.
¿Pero como leo y
escribo esto?

3. Propiedades
Condición de
existencia del log.
• No existe el logaritmo de un
número con base negativa.
• No existe el logaritmo de un

4. Función logarítmica
La función inversa de la función exponencial se
llama el “logaritmo en base a de x ”, y se denota por
¿Por qué es
inversa?
Ejemplos:
Importante: No existe el logaritmo en cualquier base de un número
negativo o cero.

5. Propiedades
El dominio es el conjunto de los números reales positivos.
El recorrido es el conjunto de los números reales.
Si a > 1, la función es creciente
Si 0 < a < 1, entonces la función es decreciente
Grafica
La curva asociada a la función logarítmica intercepta al eje de las
abscisas (x) en el punto (1,0) y nunca toca al eje Y.
a >1 0 < a <1

6. Ejemplo
Solución: Obtenemos la grafica de esta función marcando los
puntos cuyas coordenadas se enumeran en la tabla anexa
x y
-1
0
1 0
3 2

7. Aplicación
Terremotos, música y champú
En 1935 el sismólogo norteamericano charles Richter (1900-1985)
¿Qué tienen en común cosas tan dispares?
ideó una escala para comparar la fuerza de los diferentes terremotos.
En la Escala Richter la magnitud R de un terremoto se define por:
precisamente los logaritmos.
Cuando se pretende representar medidas que toman valores
muy dispares, desde muy pequeños a muy grandes, se emplea
la escala logarítmica.
Algunos ejemplos en que se utiliza:
• La escala Richter que mide la intensidad de los terremotos.
• La intensidad del sonido en belios, o el mismo pentagrama.
• El pH de una sustancia
• La magnitud de las estrellas.

8. Ejemplo Aplicación
La magnitud del famoso terremoto de San Francisco de 1906 se ha
calculado en 8.25 en la escala de Richter. En 1979 un terremoto de
magnitud 5.95 se dio en esta ciudad.
¿Cuántas veces más intenso fue en de 1906?
Solución:
Esto significa que:
Ahora, como 8.25= 2.3 + 5.95, se deduce de las leyes de exponentes que
Es decir, que el terremoto de 1906 fue aproximadamente 200 veces más
intenso que el de 1979.