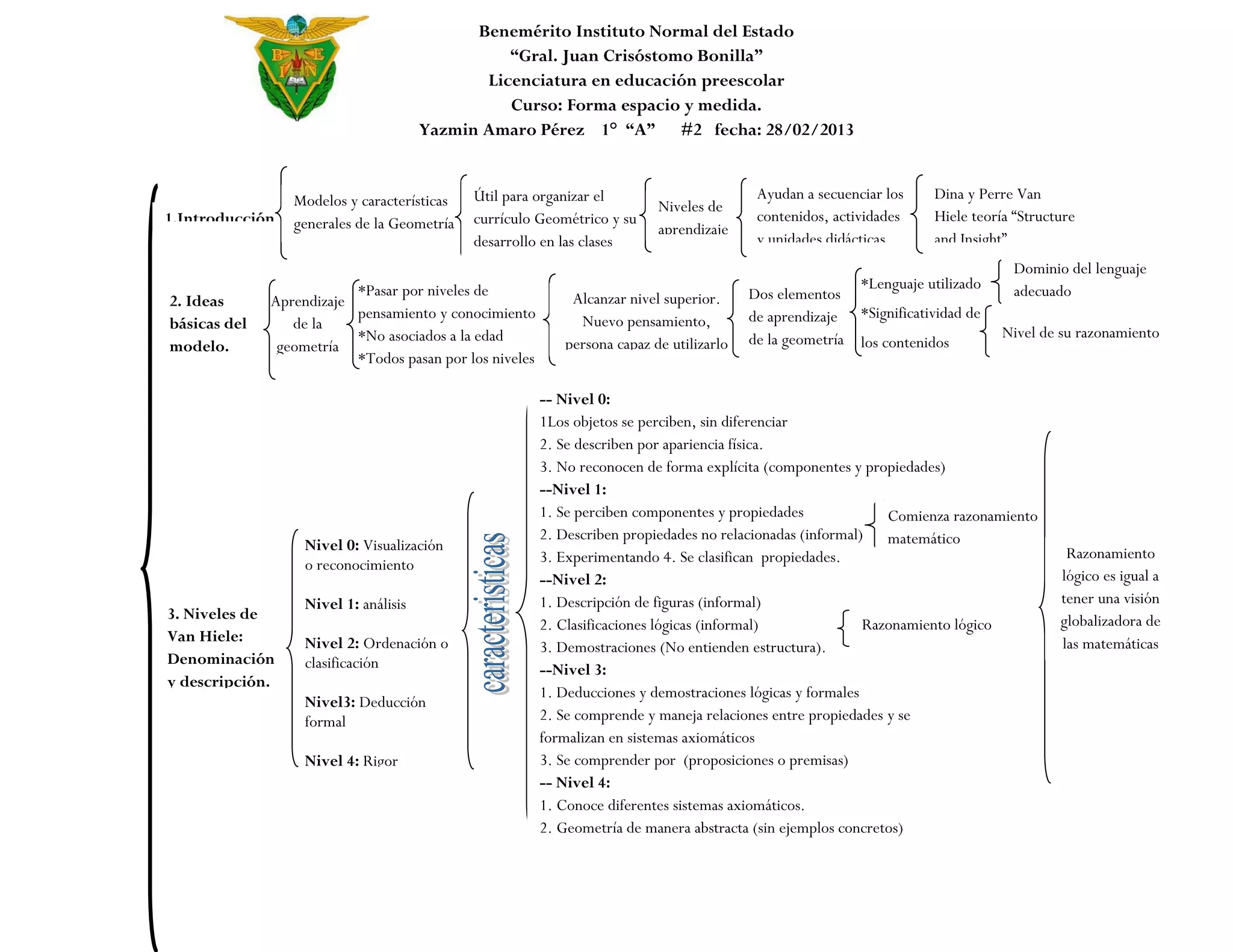
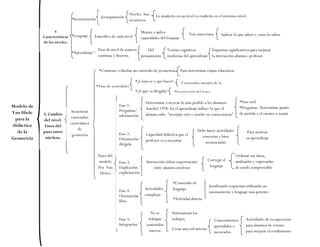
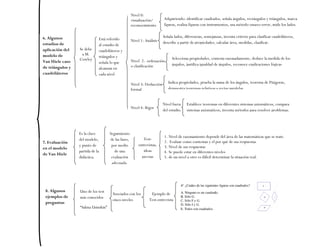
Este documento describe el modelo de Van Hiele para la enseñanza y el aprendizaje de la geometría. Explica que el modelo identifica cinco niveles de razonamiento geométrico por los que pasan los estudiantes, desde la visualización hasta la deducción formal. También cubre cómo evaluar el nivel de razonamiento de los estudiantes a través de pruebas de entrevista y diseñar currículos que se ajusten a los diferentes niveles.

1. Benemérito Instituto Normal del Estado
“Gral. Juan Crisóstomo Bonilla”
Licenciatura en educación preescolar
Curso: Forma espacio y medida.
Yazmin Amaro Pérez 1° “A” #2 fecha: 28/02/2013
1.Introducción
Modelos y características
generales de la Geometría
Útil para organizar el
currículo Geométrico y su
desarrollo en las clases
Niveles de
aprendizaje
Ayudan a secuenciar los
contenidos, actividades
y unidades didácticas.
Dina y Perre Van
Hiele teoría “Structure
and Insight”
2. Ideas
básicas del
modelo.
Aprendizaje
de la
geometría
*Pasar por niveles de
pensamiento y conocimiento
*No asociados a la edad
*Todos pasan por los niveles
Alcanzar nivel superior.
Nuevo pensamiento,
persona capaz de utilizarlo
Dos elementos
de aprendizaje
de la geometría
*Lenguaje utilizado
*Significatividad de
los contenidos
Dominio del lenguaje
adecuado
Nivel de su razonamiento
3. Niveles de
Van Hiele:
Denominación
y descripción.
Nivel 0: Visualización
o reconocimiento
Nivel 1: análisis
Nivel 2: Ordenación o
clasificación
Nivel3: Deducción
formal
Nivel 4: Rigor
-- Nivel 0:
1Los objetos se perciben, sin diferenciar
2. Se describen por apariencia física.
3. No reconocen de forma explícita (componentes y propiedades)
--Nivel 1:
1. Se perciben componentes y propiedades
2. Describen propiedades no relacionadas (informal)
3. Experimentando 4. Se clasifican propiedades.
--Nivel 2:
1. Descripción de figuras (informal)
2. Clasificaciones lógicas (informal)
3. Demostraciones (No entienden estructura).
--Nivel 3:
1. Deducciones y demostraciones lógicas y formales
2. Se comprende y maneja relaciones entre propiedades y se
formalizan en sistemas axiomáticos
3. Se comprender por (proposiciones o premisas)
-- Nivel 4:
1. Conoce diferentes sistemas axiomáticos.
2. Geometría de manera abstracta (sin ejemplos concretos)
Comienza razonamiento
matemático
Razonamiento lógico
Razonamiento
lógico es igual a
tener una visión
globalizadora de
las matemáticas

2. Modelo de
Van Hiele
para la
didáctica
de la
Geometría
4
Características
de los niveles.
*Secuenciación
*Lenguaje
*Aprendizaje
Jerarquización
Niveles. Son
recursivos
Lo implícito en un nivel es explicito en el próximo nivel.
Especifico de cada nivel
Mejora y aplica
capacidades del lenguaje
Test entrevistas Aplicar lo que saben y como lo saben
Paso de nivel de manera
continua y discreta.
Del
pensamiento
Teorías cognitivas
modernas del aprendizaje
Esquemas significativos para mejorar
la interacción alumno- profesor.
5. Cambio
del nivel.
Fases del
paso entre
núcleos.
*Construir o diseñar un currículo de geometría Para determinar etapas educativas
*Tipo de actividades
Secuenciar
contenidos
curriculares
de
geometría
*¿Cómo se y qué hacer?
*¿A qué va dirigida?
Contenidos propios de la
actividad
Presentación del tema
Fases del
modelo
Por Van
Hielen
Fase 1:
Preguntas/
información
Fase 2:
Orientación
dirigida
Fase 3:
Explicación
explicitación
Fase 4:
Orientación
libre.
Fase 5:
Integración
Determinar o acercar lo más posible a los alumnos.
Ausebel 1978: En el aprendizaje influye lo que el
alumno sabe. “averigüe esto y enseñe en consecuencia”
*Fase oral.
*Preguntas: Determinar punto
de partida y el camino a seguir
Capacidad didáctica que el
profesor va a necesitar
Debe hacer actividades
concretas y bien
secuenciadas
Para motivar
su aprendizaje
Interacción (ideas-experiencias)
entre alumno-profesor
Corregir el
lenguaje
Ordenar sus ideas,
analizarlas y expresarlas
de modo comprensible
Actividades
complejas
*Contenido de
lenguaje.
*Actividad abierta
Justificando respuestas utilizando un
razonamiento y lenguaje más potente.
No se
trabajan
contenidos
nuevos
Sistematizan los
trabajos.
Crear una red interna
Conocimientos
aprendidos o
mejorados.
Actividades de recuperación
para alumnos de retraso
para mejorar el rendimiento

3. 6. Algunos
estudios de
aplicación del
modelo de
Van Hiele caso
de triángulos y
cuadriláteros
Se debe
a M.
Cowley
Nivel 0:
visualización/
reconocimiento
Nivel 1: Análisis
Nivel 2: ordenación
o clasificación
Nivel 3: Deducción
formal
Nivel 4: Rigor
Está referido
al estudio de
cuadriláteros y
triángulos y
señala lo que
alcanzan en
cada nivel
Adquiriendo: identificar cuadrados, señala ángulos, rectángulos y triángulos, marca
figuras, realiza figuras con instrumentos, usa método ensayo-error, mide los lados.
Señala lados, diferencias, semejanzas, inventa criterio para clasificar cuadriláteros,
describe a partir de propiedades, calcular área, medidas, clasificar.
Selecciona propiedades, contesta razonadamente, deduce la medida de los
ángulos, justifica igualdad de ángulos, reconoce explicaciones lógicas
Indica propiedades, prueba la suma de los ángulos, teorema de Pitágoras,
demuestra teoremas relativos a rectas paralelas.
Nivel fuera
del estudio.
Establece teoremas en diferentes sistemas axiomáticos, compara
sistemas axiomáticos, inventa métodos para resolver problemas.
7. Evaluación
en el modelo
de Van Hiele
Es la clave
del modelo,
y punto de
partida de la
didáctica,
Seguimiento
de las fases,
por medio
de una
evaluación
adecuada.
Test-
entrevistas,
ideas
previas
1. Nivel de razonamiento depende del área de las matemáticas que se trate.
2. Evaluar como contestan y el por qué de sus respuestas
3. Nivel de sus respuestas
4. Se puede estar en diferentes niveles
5. de un nivel a otro es difícil determinar la situación real.
8. Algunos
ejemplos de
preguntas
Uno de los test
más conocidos
“Salma Usinskin”
Asociados con los
cinco niveles
Ejemplo de
Test-entrevista