Análisis Semiclásico de Operadores de Schrödinger

Análisis Semiclásico de Operadores de
Schröndinger
Juliho David Castillo Colmenares
Escuela de Ciencias, UABJO
Juliho David Castillo Colmenares Análisis Semiclásico de Operadores de Schröndinger

Planteamiento del problema
El efécto tunel
Demostración de la proposición 2.2
En la presente tesis, analizaremos el comportamiento asintótico cuando
λ → ∞ del eigenvector Ω0(x; λ), asocidado al primer eigenvalor E0(λ),
del operador ,
H (λ) = −
1
2
∆ + λ2
V (x) (1.1)
el cual actua en L2
(Rn
), y donde ∆ es el operador de Laplace y
V : Rn
→ R actua por multiplicación.

El efécto tunel
Este análisis se realizará bajo las siguientes hipotesis sobre el potencial
V : Rn
→ R:
(1) V es C∞
y no negativa;
(2) l´ım x →∞ V (x) = ∞;
(3) V se anula exactamente en dos puntos a, b y ∂2
V /∂xi ∂xj es una
matriz no singular para x = a, b.

El efécto tunel
De manera adicional, suponemos que
(4) l´ım inf
λ↑∞
( jaΩ0(λ) jbΩ0(λ) ) > 0,
donde ja, jb son funciones con soporte en vecindades muy pequeñas de a
y b.
Finalmente, pediremos que ∆V este acotado, lo que es equivalente a que
la función V : Rn
→ R sea semiconcava.

El efécto tunel
En este análisis, usaremos la métrica de Agmon, que se define de la
siguiente manera
ρ(x, y) =´ınf
1
0
2V (γ(s))| ˙γ(s)|ds γ(0) = x, γ(1) = y , (1.2)
la distancia geodésica en la métrica Riemanniana 2V (x)dx2
, conforme
con la métrica Euclidiana.

El efécto tunel
Sin embargo, usaremos una versión equivalente de la métrica de Agmon,
que es la siguiente.
Proposición
Sea ρ dada por (1.2). Entonces
ρ(x, y) = ´ınf
γ,T
1
2
T
0
|˙γ(s)|2
ds +
T
0
V (γ(s))ds γ(0) = x, γ(T) = y ,
(1.3)
donde tambien minimizamos sobre T.

El ef´ecto tunel
El resultado principal de esta tesis es el siguiente teorema
Teorema
Si se satisfacen las hiportesis (1)-(4), y si suponemos que el potencial V
es semiconcavo, entonces para cualquier x
l´ım sup
1
λ
ln |Ω0(λ; x)| = − m´ın (ρ (x, a) , ρ (x, b)) ,
siendo este l´ımite uniforme en subconjuntos compactos.

El efécto tunel
En [11] se demuestra este teorema de dos maneras diferentes: la primera,
usando el Método de Grandes Desviaciones y la segunda, con métodos de
ecuaciones diferenciales parciales. En la presente tesis, daremos una
demostración alternativa de nuestro resultado principal usando métodos
variacionales.

El efécto tunel
Este resultado tiene particular importancia en f´ısica. Nuestro estudio
considera λ → ∞, que corresponde al estudio del operador de
Schröndinger, cuando → 0, es decir, cuando consideramos como un
parametro muy pequeño, lo cual ocurre en sistemas clásicos. Por esto, se
le conoce como análisis semiclásico de operadores de Schröndinger.

El efécto tunel
Consideremos el operador de Schröndinger
H = −
2
2m
∆ + V (x), (2.1)
que actuá en L2
(Rn
), donde ∆ es el operador de Laplace y V : Rn
→ R
es una función que actua por multiplicación.

El efécto tunel
En f´ısica cuántica, se estudia la ecuación conocida como de
Schröndinger, la cuál para sistemas cuánticos estacionarios, es decir, que
no dependen del tiempo, tiene la forma
Hψ = Eψ,
donde E representa los niveles de energ´ıa de los estados cuánticos
estacionarios.

El efécto tunel
Consideremos la sustitución formal
2
m = 1
λ2 en (2.1), de lo cual se obtiene
H = −
1
2λ2
∆ + V (x), (2.2)
y a partir de (1.1), se obtiene la relación H = λ−2
H(λ). Como se puede
observar,
2
2m → 0 es equivalente a λ → ∞.

El efécto tunel
Supondremos que el potencial V cumple las hipotesis que se enunciaron
en la sección anterior. En un contexto f´ısico, se dice que un potencial que
cumple con las hipotesis (1)-(3) tiene un doble pozo en a y b, ya que a y
b son m´ınimos globales de este función. La hipotesis (4) nos dice que la
función de onda del estado base esta esencialmente concentrada en
ambos pozos (efecto tunel). La última suposición tiene sentido
f´ısicamente pues, de otra manera, las soluciones “explotar´ıan” en un
tiempo finito.

El efécto tunel
El resultado principal respecto al efecto tunel es el siguiente:
Teorema
Sea V una función en Rn
que obedece (1)-(4). Sea
H(λ) = −1
2 ∆ + λ2
V (x) y sea E1(λ), E0(λ) los dos eingenvalores más
pequeños de H(λ). Entonces
l´ım
λ→∞
−λ−1
ln [E1(λ) − E0(λ)] = ρ(a, b) (2.3)
donde ρ(a, b) es la distancia de a a b en la métrica de Agmon.

El efécto tunel
Por simplicidad, demostraremos solamente la siguiente proposición
Proposición
l´ım inf
λ→∞
−λ−1
ln [E1(λ) − E0(λ)] ≥ ρ(a, b). (2.4)
De manera informal, esta desigualdad nos dice que
E1(λ) − E0(λ) ≤ e−λρ(a,b)
,
es decir, a medida que λ → ∞, el primer estado exitado decae
exponencialmente en el estado base.

El efécto tunel
Para esta demostración, necesitaremos el teorema 1.1. De hecho,
solamente necesitaremos el siguiente hecho
Observación
Para cada > 0, existe una subsucesión {λn} , tal que
Ω(λn, x) ≤ e−λn(ρ(x)− )
(2.5)
donde ρ(x) ≡ m´ın(ρ(x, a), ρ(x, b)).

El efécto tunel
Definición
Sea
B ≡ {x|ρ(a, x) = ρ(b, x)} ,
al cual llamaremos como bisector geodésico.
Definimos
d(x) ≡
ρ(x, a) − ρ(x, b)
ρ(a, b)
, (3.1)
de manera que
d(x) =



−1 x = a
0 x ∈ B
1 x = b
(3.2)
Por la proposición 3.3 en [6], d es diferenciable cas´ı en todas parte y más
aún, podemos suponer que lo es en todas partes.

El efécto tunel
Para cualquier α > 0 fija, escogemos hα ∈ C∞
(R), con |hα| ≤ 1, y de
manera que
hα(x) =
1, x ∈ [α, ∞),
−1, x ∈ (−∞, α],
(3.3)
y hα(−x) = −hα(x). Definimos
g(x) ≡ hα(d(x)),
y notamos que g ∈ C1
(Rn
) y supp ( g) ⊂ {x| d(x) < α} , que es una
vecindad alrededor de B.

El ef´ecto tunel
Figura: Las funciones d y g, y el bisector geod˜A c sico.

El efécto tunel
Finalmente definimos, para cualquier operador A con Ω0(λ) ∈ D(A),
A λ ≡ AΩ0(λ), Ω0(λ) .
al cual llamaremos el elemento de matriz de A en el estado Ω0(λ).
Necesitamos la siguiente función,
f = g− g λ, f λ = 0, (3.4)
para la cual se tiene el siguiente
Lema
Sea E0, E1 los dos primeros eigenvalores de H(λ). Entonces
E1 − E0 ≤
1
2
| f | Ω0(λ)
2
f Ω0(λ)
−2
. (3.5)

El ef´ecto tunel
De (3.5), tenemos que
∆E ≡ l´ım inf
λ→∞
−
1
λ
ln[E1 − E0]
≥ l´ım inf
λ→∞
−
1
λ
ln | f | Ω0(λ) +
1
λ
ln f Ω0(λ) . (3.6)
N´otese que | f | = | g| , y recordemos que supp (| g|) esta localizada
en una vecindad alrededor de B. Ahora, a partir de 2.5, obtenemos
| f | Ω0(λ)
2
≤ eλn(ρ− )
Ω0(λ)
2
e−λ(˜ρ− /2)
≤ e−λ(˜ρ− /2)
, (3.7)
donde ˜ρ ≡ m´ın {ρ(x)|x ∈ supp (| g|)} .

El efécto tunel
Ahora bien, para cualquier > 0, existe una α suficientemente pequeña,
tal que
˜ρ ≥
ρ(a, b) −
2
,
ya que m´ın ρ(x)|x ∈ B = 1
2 ρ(a, b). A partir de (3.6), (2.5) y (3.7),
obtenemos que para cualquier > 0,,
∆E ≥ ρ(a, b) − + l´ım inf
λn→∞
1
λ
ln f Ω0(λ) .
Si l´ım inf(1/λ) ln f Ω0, f Ω0 < 0, entonces o bien jaΩ0 o bien jbΩ0
se hacen pequeñas, de tal manera que por la hipótesis (A4) tenemos que
l´ım inf 1
λ ln f Ω0, f Ω0 ≥ 0. Como > 0 es arbitraria, tenemos que
∆E ≥ ρ(a, b).

Introducción
Soluciones de viscosidad
Representación de las soluciones de viscosidad
Fórmula estocástica de Lax
Método de Laplace
Resultado
En nuestro problema, trabajamos con un Lagrangiano L : Rn
× Rn
→ R
de la forma
L(x, v) =
1
2
|v|2
+ V (x)
con el Hamiltoniano H : Rn
× Rn
→ R asociado
H(x, p) =
1
2
|p|2
− V (x)
donde V : Rn
→ R cumple las hipotesis (A1)-(A4). De manera adicional,
pediremos que ∆V este acotado, lo que es equivalente a que la función
V : Rn
→ R sea semiconcava.

Introducción
Método de Laplace
Resultado
Como se explicará en el la siguiente sección, para c ≥ 0, la ecuación de
Hamilton-Jacobi
1
2
|Dφ(x)|
2
− V (x) = c (4.1)
tiene soluciones φ : Rn
→ R, las cuales. para c = 0 no son soluciones
clásicas, y que en este contexto llamaremos soluciones de viscosidad.
Aunque para c = 0 existe una infinidad de soluciones que solamente
difieren por una constante, tambien existen soluciones que no solamente
difieren por esta caracteristica, si no que de hecho, depende de los valores
en a y b.

Introducción
Método de Laplace
Resultado
Consideremos ahora la ecuación de Hamilton Jacobi con viscosidad:
ε∆φ(x) +
1
2
|Dφ(x)|
2
− V (x) = c(ε), (4.2)
donde el parametro ε es el coeficiente de viscosidad. Como en el caso sin
viscosidad, existe una única constante c(ε) tal que la ecuación de
Hamilton Jacobi con viscosidad. Sin embargo, en este caso, la solución
será única, salvo una constante y la denotaremos φε.

Introducción
Método de Laplace
Resultado
De hecho, si φε es una solución de (4.2), entonces exp(φε/2ε) es una
eigenfunción del operador de Schröndinger 2ε2
∆ − V (x), con eigenvalor
c(ε).

Introducción
Método de Laplace
Resultado
Considere ahora la sustitución ε = 1/2λ. Recordemos que si λ → ∞,
entonces E0(λ)
λ →
√
ω#, esta última una constante. Entonces
c(1/2λ) → 0, cuando λ → ∞. De manera equivalente c(ε) → 0, cuando
ε → 0.

Introducción
Método de Laplace
Resultado
Observación
A partir de ahora, por los argumentos anteriores, trabajaremos con la
notación ψε(x), para referirnos al estado base Ω(λ; x). Debemos tener
presente las relaciones 2ε = 1
λ y φε = eψε/2ε
.

Introducción
Método de Laplace
Resultado
Para obtener la demostración del teorema 1.1, estudiaremos el
comportamiento de φε cuando ε → 0, de manera que podamos obtener
subsucesiones que convergen uniformemente y, aplicando el método de
Laplace, obtendremos el resultado deseado. De hecho, obtendremos la
métrica de Agmon como una expresión del l´ımite de φε, en terminos de a
y b.

Introducción
Método de Laplace
Resultado
Definición
Una función continua φ : Rn
→ R se dice solución de viscosidad hacia el
futuro de la ecuación (4.1) si satisface las siguientes propiedades:
1 Si v ∈ C1
y φ − v tiene un m´ınimo local en x entonces
1
2
|Dv(x)|
2
− V (x) ≥ 0,
2 Si v ∈ C1
y φ − v tiene un máximo local en x entonces
1
2
|Dv(x)|
2
− V (x) ≤ 0.

Introducción
Método de Laplace
Resultado
De hecho, una función es una solución de viscosidad adelantada de (4.1)
si y solo si resuelve el siguiente problema de punto fijo, para toda
x ∈ Rn
, t ≥ 0,
v(x) = sup
γ:[0,t]→Rn,γ(0)=x
{v(γ(t)) −
t
0
1
2
|˙γ(s)|
2
+ V (γ(s))ds} (5.1)
donde el supremo se toma sobre las curvas C1
a trozos. Esta fórmula es
conocida como de Lax-Oleinik o principio de programación dinámica.

Introducción
Método de Laplace
Resultado
De hecho, como lo veremos en la siguiente sección, la solución esta dada
por
φ(x) = máx{φ(a) − ρ(x, a), φ(b) − ρ(x, b)}. (5.2)

Introducción
Método de Laplace
Resultado
Definamos, para toda y ∈ Rn
,
ζ(y) =´ınf
t
0
1
2
|˙γ(s)|
2
+ V (γ(s))ds|t ≥ 1, γ(0) = γ(t) = y ,
y entonces, definimos el conjunto de Aubry A como
A = {y ∈ Rn
|ζ(y) = 0} .
Como ζ(y) ≥ V (y), y entonces, ζ(y) = 0 ⇐⇒ y = a, b, es claro que
A = a, b.

Introducción
Método de Laplace
Resultado
Definimos S como el conjunto de soluciones de viscosidad, y para
φ ∈ S , definimos E (v) como el conjunto de curvas absolutamente
continuas γ, que satisfacen para r < t,
φ(γ(t)) = φ(γ(r)) + ρ(φ(r), φ(t)).

Introducción
Método de Laplace
Resultado
Lema
Sea φ ∈ S y γ ∈ E . Existe una función Ψ ∈ S de manera que
φ(γ(t)) − ρ(·, γ(t)) → Ψ in C(Rn
),
cuando t → ∞.
Más aún, Ψ = φ en γ([0, ∞)) y Ψ ≤ φ en Rn
.

Introducción
Método de Laplace
Resultado
Denotaremos por g(φ, γ), la función Ψ ∈ S que obtuvimos en el lema
anterior. Es decir,
g(φ, γ)(x) = l´ım
t→∞
[φ(γ(t)) − ρ(x, γ(t))] para x ∈ Rn
.

Introducción
Método de Laplace
Resultado
Teorema (Fórmula de representación de soluciones de viscosidad)
Sea φ ∈ S . Entonces, para toda x ∈ Rn
,
φ(x) = sup {g(φ, γ)(x)|γ ∈ E } .

Introducción
Método de Laplace
Resultado
Observación
Para φ ∈ S , no es existe γ ∈ E , tal que l´ımt→∞ |γ(t)| = ∞.
Por tanto, la fórmula de representación se reduce a
φ(x) = máx {φ(a) − ρ(x, a), φ(b) − ρ(x, b)} .

Introducción
Método de Laplace
Resultado
La solución a la ecuación de viscosidad (4.2) puede ser caracterizada por
una fórmula variacional análoga a (5.1). En el caso viscoso, necesitamos
introducir un movimiento Browniano W (t) : Ω → Rn
. Denotaremos por
E la esperanza con respecto a la medida de probabilidad P.

Introducción
Método de Laplace
Resultado
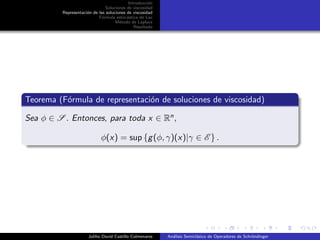
La solución a la ecuación (4.2) satisface la fórmula de Lax
φε(x) = sup
v
E φε(Xε(τ)) −
τ
0
1
2
|v(s)|
2
+ V (Xε(s))ds − c(ε)τ ,
(7.1)
donde v es un control admisible progresivamente medible, τ es un tiempo
de paro finito y Xε es la solución de la ecuación diferencial estocástica
dXε(t) = v(t)dt + (2ε)dW (t)
Xε = x,
(7.2)
que se deduce del lema 3.1 en [5].

Introducción
Método de Laplace
Resultado
El supremo en (7.1) se alcanza y el control óptimo se obtiene de la
siguiente manera. Si consideramos la solución del siguiente ecuación
diferencial estocástica
dXε(t) = Dφε(Xε(t))dt + (2ε)dW (t)
Xε = x,
(7.3)
entonces el control óptimo esta dado por la siguiente fórmula
v(t) = Dφε(Xε(t)).

Introducción
Método de Laplace
Resultado
El siguiente lema se puede probar usando la Fórmula de Lax y la última
hipotesis que introdujimos, es decir, que V es semiconcavo.
Lema
Las soluciones φε de (4.2) son Lipschitz y semiconvexa uniformemente en
ε, en compactos. Entonces, adicionando una condición de
“normalización”, como φε(x0) = 0, siempre existen subsucesiones que
convergen en la norma C0
.

Introducción
Método de Laplace
Resultado
Teorema
[9] Sea fn una suceción de funciones diferenciables convexas que
convergen puntualmente a una función diferenciable f . Entonces Dfn
convege puntualmente a Df , y en compactos, lo hace uniformemente.

Introducción
Método de Laplace
Resultado
Una aplicación inmediata de este lema (y del teorema que se enunció) es
el siguiente
Lema
Suponga que la sucesión φεn de soluciones de (4.2) converge C0
a φ0.
Supongamos que φ0 es diferenciable en un abierto V . Entonces dφεn
converge a dφ0 uniformemente en cada subconjunto compacto de V .

Introducción
Método de Laplace
Resultado
Recordemos que las solución de viscosidad de (4.1) esta dada por
φ(x) = máx{φ(a) − ρ(x, a), φ(b) − ρ(x, b)}.
En esta sección, mostraremos que φ(a) = φ(b), usando el método de
Laplace. Este se puede enunciar de la siguiente manera

Introducción
Método de Laplace
Resultado
Lema (Método de Laplace)
Suponga que l : Rn
→ R es una función continua que crece a los más
linealmente, y que k : Rn
→ R es una función continua, dos veces
diferenciable en una vecindad de y0 ∈ Rn
, de manera que
k(y0) = m´ın
y∈R
k(y).
Entonces
l´ım
ε→0
Rn l(y)e
−k(y)
ε dy
Rn e
−k(y)
ε dy
= l(y0).

Introducción
Método de Laplace
Resultado
Primero observemos que ∀γ ∈ Cac
(x, y) : A(γ) ≥ 0, por lo que
h(x, y) ≥ 0. De donde, a, b son máximos locales de φ(x). De hecho, por
la forma de la solución, por lo menos uno deber´ıa ser máximo global.

Introducción
Método de Laplace
Resultado
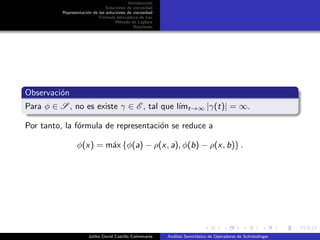
Ahora bien, supongamos que φ(a) > φ(b). Entonces a es un máximo
global. Como en una vecindad de a, φ es C3
, (por el lema 1 en [9]) y a
máximo local, por el teorema de Taylor, φ tiene decrecimiento por lo
menos cuadrático. Entonces, podemos aplicar el método de Laplace y
después de unos cálculos, obtenemos
l´ım
ε→0 Rn
l(y)ψ2
ε(y)dy = l(a).

Introducción
Método de Laplace
Resultado
En particular si B = {x : |x − b| < δ}, para δ > 0 suficientemente
pequeño, y χ una partición de la unidad, con soporte conteniendo a B,
tenemos que
0 = χB (a)
= l´ım
ε→0 Rn
χB (y)ψ2
ε(y)dy
= l´ım inf
λ→∞
jb(Ω) ,
donde ja es una función de soporte en B. esto contradice la hipotesis
(A4). Por lo cual, tenemos que φ(a) = φ(b).

Introducción
Método de Laplace
Resultado
Con esto, hemos obtenido el resultado deseado. Como φ(a) = φ(b),
podemos normalizar de manera que ambas constantes sean iguales a
cero. Ahora bien, nuestra solución
φ(x) = l´ım
εn→0
φεn
.
Pero
φεn
= 2εn ln ψεn
.

Introducción
Método de Laplace
Resultado
Recordemos que ψεn es el estado base Ω(λ; x) de 1.1, y de hecho,
haciendo 2εn = 1
λ ,
εnψεn =
1
λ
Ω(λ; x)(x).
Entonces, bajo las hipotesis (A1)-(A4), además de suponer que la función
V : Rn
→ R es semiconcava, hemos demostrado que
l´ım
λ→∞
1
λ
Ω(λ; x) = máx (−ρ(x, a), −ρ(x, b))
= − m´ın (ρ(x, a), ρ(x, b)) .

Ideas principales
Aportaciones
El efecto túnel puede ser analizado al estudiar el v´ınculo entre
mecánica clásica y mecánica cuántica, ya que el comportamiento de
un sistema clásico puede verse como el l´ımite de un sistema cuántico
cuando → 0. Esto se conoce como análisis semiclásico.
El v´ınculo entre mecánica cuántica y mecánica clásica se entiende
mejor, al usar la fórmulación por integral de caminos de Feynman. A
través de esta, podemos observar como la mecánica cuántica esta
relacionada con la teor´ıa de procesos estocásticos. En especial con
procesos de difusión, que vienen de problemas en sistemas clásicos.
La soluciones de viscosidad son una técnica relativamente reciente
para resolver ecuaciones diferenciales. A través de está técnica,
hemos podido estudiar el comportamiento de sistemás clásico y
vincularlos con un problema de mecánica cuántica.

Ideas principales
Aportaciones
Por un lado, se explicó el trabajo realizado por B. Simon en [11], de
manera que un alumno sin estudios de posgrado pueda enteder el
problema, y se han explicado las herramientas utilizadas, de manera que
pueda interesarse en el estudio de tales técnica, tanto por su útilidad en
la f´ısica matemática, como en la matemática pura, en especial, en el
estudio de las ecuaciones diferenciales. Además, se presentan los terminos
de la f´ısica, de manera que un un estudiante de matemáticas pueda darse
cuenta de las posibles aplicaciones de sus conocimientos.

Ideas principales
Aportaciones
Por otro lado, una aportación importante fue emplear métodos
variacionales, en especial, los relacionados con soluciones de viscosidad,
para resolver un problema que se hab´ıa tratado con algunas otras
técnicas. La importancia de abordar el problema desde esta perspectiva
es que este tema, que se ha empezado a investigar de manera reciente,
ha sido ya utilizado ampliamente para resolver muchos otros problemas
en ecuaciones diferenciales, pues echa mano de la teor´ıa del control
estocástico, el cual ha sido ampliamente desarrollado. Por lo cual, ofrece
una perspectiva rica y diferente de un problema importande en f´ısica.

Ideas principales
Aportaciones
Contreras, Gonzalo, Iturriaga, Renato; Global Minimizers of
Autonomous Lagrangians;
www.cimat.mx/ gonzalo/libro/lagrangians.pdf.
Evans, Lawrence; An Introduction to Stochastic Differential
Equations; http://math.berkeley.edu/ evans/SDE.course.pdf.
Evans, Lawrence; An Introduction to Mathematical Optimal Control
Theory; http://math.berkeley.edu/ evans/control.course.pdf.
Evans, Lawrence; Partial Differential Equations; American
Mathematical Society.
Fleming, W., Soner, M.; Controlled Markov Processes and Viscosity
Solution; Springer, 1993.
Hislop, Israel; Sigal, Michael; Introduction to Spectral Analysis: with
applications to Schrödinger operators; Springer Verlag Inc., 1996.

Ideas principales
Aportaciones
Ichihara, Naoyuki; Ishii, Hitoshi; Long-time Behavior of Solutions of
Hamilton-Jacobi Equations with Convex and Coercive Hamiltonians;
Arch. Rational Mech. Anal. 194 (2009) 383-419.
Rudin, Walter; Real and Complex Analysis; McGraw-Hill, 1970.
Sánchez-Morgado, Héctor, et.al.; Physical solutions of the
Hamilton-Jacobi Equation; Discrete and Continuous Dynamical
Systems- Series B, Vol. 5, No. 3; 2005, pag 513-528.
Simon, Barry; Semiclassical analysis of low lying eigenvalues, I.
Non-degenerate minima: asymptotic expansions; Annales de lâI. H.
P., sección A, tomo 38, no. 3 (1983), p. 295-308.
Simon, Barry; Semiclassical analysis of low lying eigenvalues, II.
Tunneling; Annals of Mathematics, 120(1984), pag 89-118.
Simon, Barry; Functional analysis and quantum mechanics;
Academic Press Inc, 1979.

Ideas principales
Aportaciones
Simon, B., Reed, M.; Methods of Modern Mathematical Physics,
Vol. I; Academic Press, 1979.
Strocchi, F.; An introduction to the Mathematical Structure of
Quantum Meechanics; Advanced Series in Mathematical Physics,
Vol. 27, World Scientiﬁc, 2005.

Análisis Semiclásico de Operadores de Schrödinger

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Análisis Semiclásico de Operadores de Schrödinger

Más de Juliho Castillo

Análisis Semiclásico de Operadores de Schrödinger