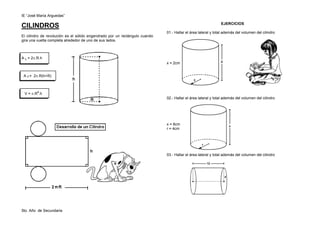
El documento presenta una serie de ejercicios relacionados con el cálculo del área lateral, área total y volumen de cilindros. Se proporcionan las fórmulas para calcular estas medidas y varios problemas con valores numéricos dados para hallar estas cantidades.

1. IE “José María Arguedas”
EJERCICIOS
CILINDROS
01.- Hallar el área lateral y total además del volumen del cilindro
El cilindro de revolución es el sólido engendrado por un rectángulo cuando
gira una vuelta completa alrededor de uno de sus lados.
A L = 2 .R.h
x = 2cm
A T = 2 .R(h+R)
2
V = .R .h
02.- Hallar el área lateral y total además del volumen del cilindro
x = 8cm
r = 4cm
03.- Hallar el área lateral y total además del volumen del cilindro
5to. Año de Secundaria

2. IE “José María Arguedas”
04.- Hallar el área lateral y total además del volumen del cilindro
07.- Hallar el volumen del sólido
05.- Hallar el área lateral y total además del volumen del cilindro
08.- Hallar el volumen del sólido
06.- Hallar el área lateral y total además del volumen del cilindro
09.- Encontrar el área de la superficie total de un cilindro de revolución, el
radio de su base mide 2cm y su altura mide 5cm
a) 28 cm
2
b) 24 cm
2
c) 32 cm
2
d) 36 cm
2
e) 20 cm
2
x = 7cm
10.- Calcular el radio de la base de un cilindro de revolución si su volumen es
3
2000 cm y su altura mide 20cm.
a) 5cm
5to. Año de Secundaria
b) 20cm
c) 10cm
d) 15cm
e) 2,5cm