Este documento resume los pasos para analizar una transformación lineal definida por una matriz dada. Se identifican el vector genérico, el núcleo, los autovalores y autovectores de la transformación. Luego, se construyen las matrices P y D para verificar si la transformación es diagonalizable. Finalmente, se grafican los resultados y se plantea la transformación inversa.

1. Gustavo Zamar
Sofía Torres
ACTIVIDAD 5 MATEMATICA I
ACTIVIDAD D
Seleccione con su grupo una matriz de la lista. A partir de esta matriz construya una transformación
matricial (transformación lineal –TL-) asociada. Luego explicite: (sea muy cuidadoso con la simbología
matemática):
a) El vector genérico TX.
b) El núcleo de esta TL.
c) Los autovalores de la TL.
d) Una base de los autovectores asociados a cada autovalor.
Además:
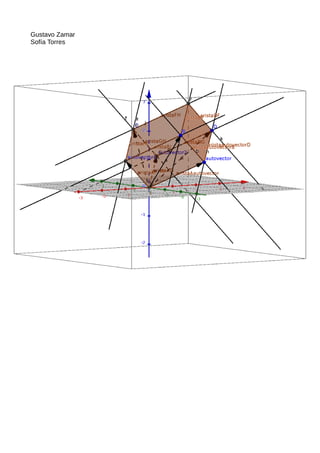
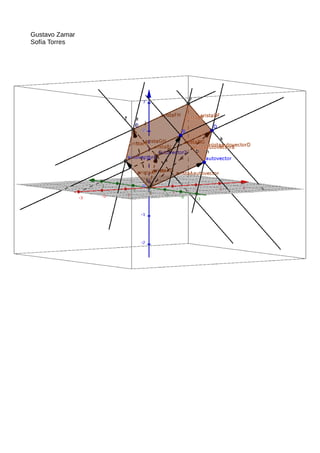
e) Grafique cada vector de cada base y también grafique cada espacio generado.
f)Analice si A es diagonalizable. En caso de serlo construya P y D que hacen verdadera la igualdad. Para
pensar: ¿Cómo y con qué información se construyen dichas matrices?
h)Plantee la transformación inversa.
1 1 0
10 1 2 1
0 1 1
A
− 
 = − − 
 − 
TRANSFORMACIÓN: TX
1 1 0
10 1 2 1
0 1 1
A
− 
 = − − 
 − 
[x
y
z] =
[ x−y
−x+2 y−z
−y+z ]
NUCLEO DE LA TRANSFORMACION
Para calcularlo planteamos el SELH:
x−y=0
−x+2 y−z=0 y tiene la matriz ampliada
[1 −1 0 0
−1 2 −1 0
0 −1 1 0]
−y+z=0
cuya resolución por el método de reducción Gauss-Jordan nos devuelve como resultado :
VECTOR
GENERICO TXMatriz de
transformación

2. Gustavo Zamar
Sofía Torres
entonces el núcleo sería :
[
0
0
0]
Lo que implica que el núcleo de la transformación sólo admite el vector nulo.
AUTOVALORES DE LA TRANSFORMACIÓN
AX=kX
[1 −1 0
−1 2 −1
0 −1 1 ] .
[x
y
z]=k
[x
y
z ] →
x−y=kx
−x+2 y−z=ky
−y+z=kz
→
x(1−k)−y=0
−x+ y(2−k)−z=0
−y+ z(1−k)=0
|1−k −1 0
1 2−k −1
0 −1 1−k
|=0 → (2−k)(1−k)+1+(1−k)+1=0 → k
2
−4k+3=0
resolviendo la ecuación cuadrática tenemos su forma factorizada con la raíces: (x−1)(x−3)
y los autovalores serán 1 y 3.

3. Gustavo Zamar
Sofía Torres
BASE DE AUTOVECTORES
Para determinar todos los autovectores de A asociados a los autovalores anteriormente
mencionamos debemos desarrollar la siguiente igualdad
AX =kX donde k es el autovalor asociado a la matriz.
Tenemos para el auto valor 1:
[
1 −1 0
−1 2 −1
0 −1 1 ] [
x
y
z] = 1
[
x
y
z] Entonces tenemos
[
x−y=x
−x+2 y−z=y
−y+z=z ] =
[ x−y−x=0
−x+2 y−z−y=0
−y+z−z=0 ]
Luego: s
[ y=0
−x+ y−z=0
−y=0 ] simplificando tenemos que [ −y=0
−x+ y−z=0]
y reemplazando −x+0−z=0→x=−z por lo tanto, un autovector asociado al autovalor 1 sería:
[−z
0
z ] o, lo que es lo mismo decir: z
[
−1
0
1 ]
Luego, para determinar el autovector asociado al autovalor 3:
[1 −1 0
−1 2 −1
0 −1 1 ] [
x
y
z] = 3
[
x
y
z] Entonces tenemos
[ x−y=3 x
−x+2 y−z=3 y
−y+z=3 z ] =
[ x−y−3 x=0
−x+2 y−z−3 y=0
−y+z−3 z=0 ]
Luego:
[−2x−y=0
−x−y−z=0
−y−2z=0 ] −y=2z→ y=−2z
−x+2 z−z=0→−x+z=0→ x=z
−2 z+2z=0
con lo cual tenemos que el
autovector quedaría
[ z
−2 z
z ] o lo que es lo mismo z
[1
−2
1 ]

4. Gustavo Zamar
Sofía Torres
Luego, para determinar el autovector asociado al autovalor 0:
[1 −1 0
−1 2 −1
0 −1 1 ] [
x
y
z] = 0
[
x
y
z] Entonces tenemos
[ x−y=0 x
−x+2 y−z=0 y
−y+z=0z ] Luego: −x+2 z−z=0→−x+z=0→x=z
− y+z=0→ y=z
con lo cual tenemos que el autovector quedaría
[
z
z
z] o lo que es lo mismo z
[
1
1
1]
DIAGONALIZACION
Construimos la matriz P con los autovectores obtenidos y verificamos si ésta admite inversa:

5. Gustavo Zamar
Sofía Torres
construimos la matriz D con los autovalores
[0 0 0
0 3 0
0 0 1] y
hacemos A=PDP
−1
y efectivamente nos devuelve la matriz A. Lo que implica que A sí es diagonalizable. Y las diferencias que
observamos se deben a las aproximaciones decimales utilizadas para poder operar con las calculadoras.
Gráfica adjunta en la pagina siguiente.
Inversa de
P
PD
P*D

6. Gustavo Zamar
Sofía Torres

7. Gustavo Zamar
Sofía Torres