1) Un ingeniero necesita conocer la posición de unas bancas ubicadas en una plaza. Ubica un teodolito en el centro y observa ángulos entre las bancas.
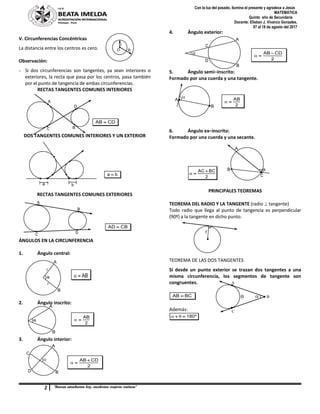
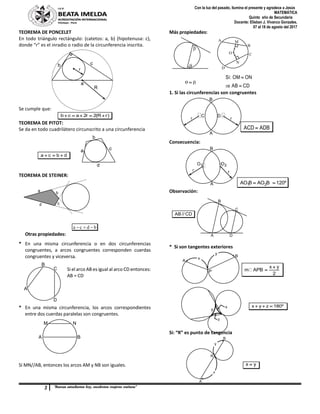
2) Se presentan definiciones y propiedades de la circunferencia como elementos, ángulos, teoremas y más.
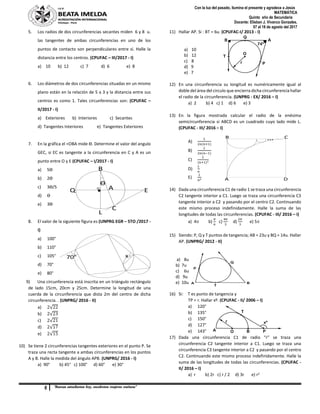
3) Se plantea una situación de aprendizaje sobre ángulos en la circunferencia y ejercicios para aplicar conceptos.