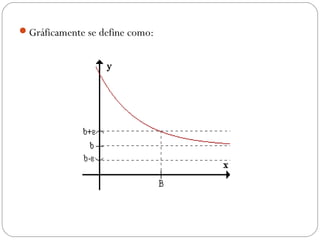
El documento presenta conceptos sobre límites al infinito y derivadas. Define límite al infinito como el valor al que se aproxima una función cuando la variable tiende a infinito. Explica que la derivada representa cómo se modifica una función cuando su variable cambia y corresponde a la pendiente de la tangente en un punto. Como ejemplo, resuelve un problema sobre la velocidad máxima de un coche entre 0 y 2 horas.

1. Presentado por : Brandon Rico Cáceres
Ingeniería de Sistemas
Calculo II
profesora : María Eugenia Montero
Trabajo de :
Limites al Infinito & Derivadas

2. Limites al Infinito
En matemática, se le llama asíntota de la gráfica de una
función, a una recta a la que se aproxima continuamente la
gráfica de tal función;1
es decir que la distancia entre las dos
tiende a ser cero (0), a medida que se extienden
indefinidamente.
O que ambas presentan un comportamiento asintótico.
Generalmente, las funciones racionales tienen
comportamiento asintótico

3. DEFINICIÓN:
Diremos que b es el límite de la función f(x) cuando x
tiende a más infinito, cuando sea cual sea el valor del
número positivo ε, es posible encontrar un número real, B,
tal que si x es mayor que B, entonces la distancia entre f(x)
y b es menor que ε.
Simbólicamente esta definición se representa así:

4. Gráficamente se define como:

5. DEFINICIÓN:
Sea f una función con dominio k tal que para cualquier
número c , existen elementos de k en el intervalo <- inf; c >.
El límite de f (x) cuando x tiende a menos infinito es L , que
se representa
si para todo ε >0 existe un número M tal que para cada y .

6. Que es un Derivada
del latín deriv tusā , derivada es un término que puede
utilizarse como sustantivo o como adjetivo. En el primer
caso, se trata de una noción de la matemática que nombra
al valor límite del vínculo entre el aumento del
valor de una función y el aumento de
la variable independiente.

7. Que Representa una Derivada
La derivada, por lo tanto, representa cómo se modifica una
función a medida que su entrada
también registra alteraciones. En los casos de las funciones
de valores reales de una única variable, la derivada
representa, en un cierto punto, el valor de la pendiente de
la recta tangente al gráfico de la función en dicho punto.

8. Ejemplos de Derivadas

9. Ejercicio aplicativo
Un coche de competición se desplaza a una velocidad que, entre las 0 y 2 horas, viene dada por la expresión v(x)= (2-x).ex
, donde x es
el tiempo en horas y v(x) es a velocidad en cientos de kilómetros. Hallar en que momento del intervalo circula a la velocidad
máxima y calcular dicha velocidad. ¿En que periodos gano velocidad y en cuales redujo? ¿Se detuvo alguna vez?
SOLUCIÓN
Nos piden q estudiemos el crecimiento y decrecimiento y el máximo de la función velocidad v.
Por eso utilizamos la derivada, ya que sabemos (por teoría) que si la derivada da positiva la función crece y si da negativa decrece.
También sabemos que, la función tiene un máximo relativo en un punto, si la derivada, en ese punto, es 0 (condición necesaria) y
además cambia el crecimiento (es decir pasa de crecer a decrecer)
La derivada es:
 v’(x)=-1.ex
+ ex
.(2-x)= -ex
+ 2 ex
- x .ex
= ex
- x. ex
, sacando factor común ex
se llega a: v’(x)=((1-x)ex
 Igualando a 0 nos da (1-x).ex
=0, de donde 1-x =0 y por tanto x =1, (ya q ex
nunca puede ser cero)
 Estudiamos v en los alrededores de 1
 v ‘ + 1 - 2
 y crece decrece
 Por lo tanto en x=1 hay máximo y la función crece de 0 a 1 (gana velocidad) y decrece de 1 a 2 (reduce velocidad), veamos los
valores en ese punto y en el extremo:
 v(x)= (2-x)ex
 v(1)=(2-1).e = e (aquí el máximo como justificamos antes)
 v(0)=(2-0).1=2
 v(2)=(2-2).1=0 como da la velocidad 0 aquí se detuvo.

10. Ejercicio aplicativo
Un coche de competición se desplaza a una velocidad que, entre las 0 y 2 horas, viene dada por la expresión v(x)= (2-x).ex
, donde x es
el tiempo en horas y v(x) es a velocidad en cientos de kilómetros. Hallar en que momento del intervalo circula a la velocidad
máxima y calcular dicha velocidad. ¿En que periodos gano velocidad y en cuales redujo? ¿Se detuvo alguna vez?
SOLUCIÓN
Nos piden q estudiemos el crecimiento y decrecimiento y el máximo de la función velocidad v.
Por eso utilizamos la derivada, ya que sabemos (por teoría) que si la derivada da positiva la función crece y si da negativa decrece.
También sabemos que, la función tiene un máximo relativo en un punto, si la derivada, en ese punto, es 0 (condición necesaria) y
además cambia el crecimiento (es decir pasa de crecer a decrecer)
La derivada es:
 v’(x)=-1.ex
+ ex
.(2-x)= -ex
+ 2 ex
- x .ex
= ex
- x. ex
, sacando factor común ex
se llega a: v’(x)=((1-x)ex
 Igualando a 0 nos da (1-x).ex
=0, de donde 1-x =0 y por tanto x =1, (ya q ex
nunca puede ser cero)
 Estudiamos v en los alrededores de 1
 v ‘ + 1 - 2
 y crece decrece
 Por lo tanto en x=1 hay máximo y la función crece de 0 a 1 (gana velocidad) y decrece de 1 a 2 (reduce velocidad), veamos los
valores en ese punto y en el extremo:
 v(x)= (2-x)ex
 v(1)=(2-1).e = e (aquí el máximo como justificamos antes)
 v(0)=(2-0).1=2
 v(2)=(2-2).1=0 como da la velocidad 0 aquí se detuvo.