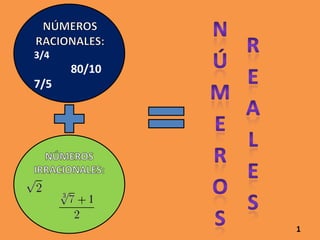
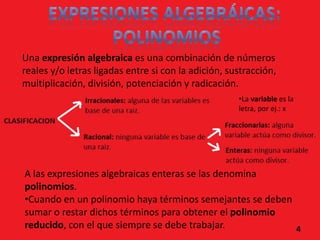
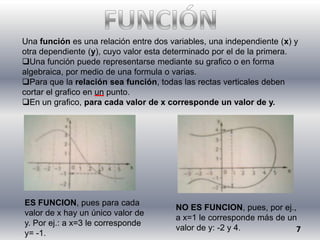
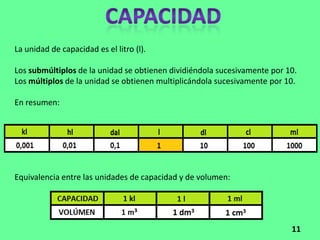
El documento presenta información sobre números reales, racionales e irracionales, expresiones algebraicas, ecuaciones, funciones y proporcionalidad. Explica que los números reales incluyen a los racionales e irracionales, y que una expresión algebraica combina números y letras con operaciones. También define conceptos como ecuación, función, proporción y sistema de ecuaciones.

1. 3/4
80/10
7/5
1

2. Un numero es irracional cuando no puede ser
expresado como el cociente entre dos números
enteros; y su expresión decimal tiene una cantidad
infinita de cifras decimales. Ej.:
• Todas las raíces no exactas:
• El número pi: 3,141592654…
Un numero racional es todo número que puede
representarse como el cociente de dos números
enteros, es decir, una fracción común.
Con los números reales podemos realizar todas
las operaciones, excepto la radicación de índice par
y radicando negativo, y la división por cero.
A todo número real le corresponde un punto de
la recta y a todo punto de la recta un número real.2

3. Es una forma de escribir
números muy grandes o
muy pequeños.
Se utiliza para poder
expresarlos de una manera
abreviada y operar con
mayor facilidad. Ej.:
•5000 = 5.1000 = 5.103
•0,02 = 2 = 2. 1 = 2.10-2
100 100
3

4. Una expresión algebraica es una combinación de números
reales y/o letras ligadas entre si con la adición, sustracción,
multiplicación, división, potenciación y radicación.
•La variable es la
letra, por ej.: x
A las expresiones algebraicas enteras se las denomina
polinomios.
•Cuando en un polinomio haya términos semejantes se deben
sumar o restar dichos términos para obtener el polinomio
reducido, con el que siempre se debe trabajar. 4

5. Ejemplo:
P(x) = 3x3 – 6x + 2x2 + 10x + 3 – 7x2 = 3x3 + 4x + 3 – 5x2
•Los números que multiplican a las indeterminadas se denominan
coeficientes: 3, 4, 3, 5.
•El grado (GR) es el mayor exponente de todas sus indeterminadas:
3.
•El coeficiente principal (CP) es el que multiplica a la indeterminada
de mayor exponente: 3.
•El termino independiente (TI) es el que no esta multiplicado por
ninguna indeterminada: 3.
5

6. Una ecuación es una igualdad entre dos miembros,
en donde aparece una incógnita: x. Ej.:
Verificamos, reemplazando x por el valor obtenido:
2x + 4 = 8 2 . 2 + 4 =8
2x = 8 – 4 4+4=8
x=4:2 8=8
x=2
Las inecuaciones son expresiones algebraicas en
donde no se plantea una igualdad. Se resuelven
como las ecuaciones, salvo que se multiplique o
divida por un numero negativo; en dicho caso,
cambia el sentido de la desigualdad. Ej.:
(1 – 2x) : 3 < 5
1 – 2x < 15
-2x < 14
6
x > -7

7. Una función es una relación entre dos variables, una independiente (x) y
otra dependiente (y), cuyo valor esta determinado por el de la primera.
Una función puede representarse mediante su grafico o en forma
algebraica, por medio de una formula o varias.
Para que la relación sea función, todas las rectas verticales deben
cortar el grafico en un punto.
En un grafico, para cada valor de x corresponde un valor de y.
ES FUNCION, pues para cada
NO ES FUNCION, pues, por ej.,
valor de x hay un único valor de
a x=1 le corresponde más de un
y. Por ej.: a x=3 le corresponde
valor de y: -2 y 4. 7
y= -1.

8. Una razón es la expresión del cociente entre dos números reales. Ej.:
Dados 4 números reales a, b, c y d en un cierto orden y distintos de 0; se
dice que forman proporción cuando la razón entre los dos primeros es
igual a la razón entre los dos segundos.
PROPIEDAD FUNDAMENTAL
En toda proporción, el producto de los medios es igual al producto de los
extremos:
Ej.:
8

9. Si tres o mas rectas paralelas
(A, B, C y D) son cortadas por
dos transversales (E y F),
quedan determinados en
ambas transversales varios
segmentos (nr, rp, gm, ms, etc.)
Los segmentos homólogos son
los que se encuentran entre
dos paralelas y uno en cada
transversal. Por ej.: nr y gm son
homólogos y también lo son ro
y ms.
“Teorema de Thales” – Les Luthiers 9

10. La unidad de volumen es 1 m3.
Los submúltiplos de la unidad se obtienen dividiéndola sucesivamente por
1000.
Los múltiplos de la unidad se obtienen multiplicándola sucesivamente por
1000.
En resumen:
10

11. La unidad de capacidad es el litro (l).
Los submúltiplos de la unidad se obtienen dividiéndola sucesivamente por 10.
Los múltiplos de la unidad se obtienen multiplicándola sucesivamente por 10.
En resumen:
Equivalencia entre las unidades de capacidad y de volumen:
11

12. •Mauro Islas Abdenur
•Carla Aramayo
•Gonzalo Suárez
•Lucía Abdenur
•Paula Albornos
3ro 1ra Economía
Bibliografía: Matemática 3/9 – Kapeluz NORMA
www.ditutor.com
12