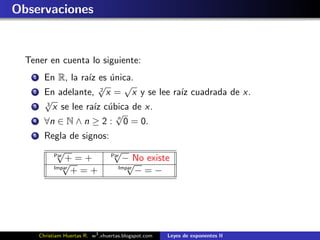
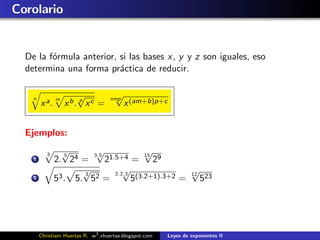
Este documento presenta las leyes de exponentes y radicación. Explica conceptos como raíces, exponentes fraccionarios y operaciones con raíces como suma, multiplicación y raíces sucesivas. Incluye definiciones, teoremas y ejemplos para ilustrar las propiedades y aplicaciones de las leyes de exponentes y radicación. Finalmente, propone algunos ejercicios para aplicar lo explicado.