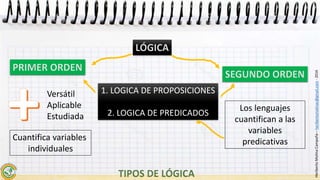
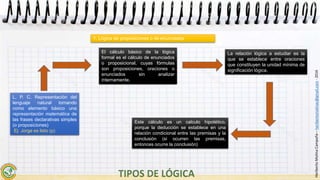
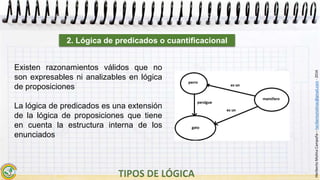
Este documento resume los conceptos fundamentales de la lógica de predicados. Explica que la lógica de predicados analiza las oraciones en sujeto y predicado y permite cuantificar sobre individuos mediante cuantificadores como "todos" y "algunos". También introduce predicados que expresan propiedades o relaciones, y extiende la lógica de proposiciones para representar razonamientos no expresables en esta. Finalmente, resume que la lógica de predicados es una lógica categorial donde se estudian las relaciones de pertenencia o poses