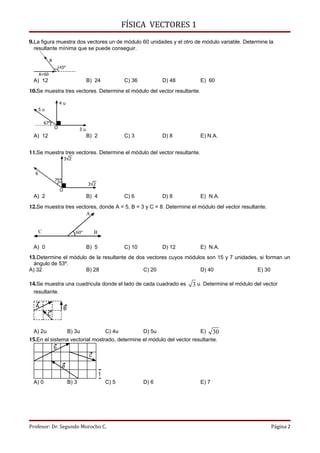
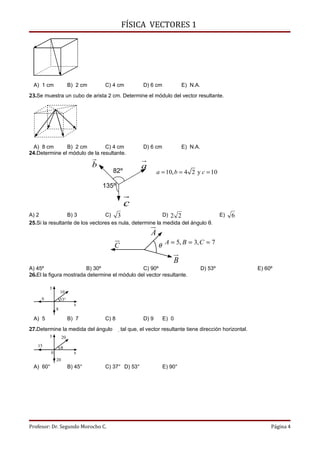
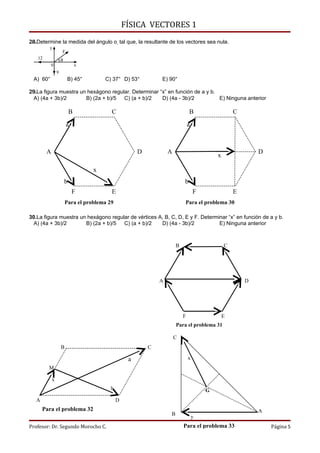
Este documento presenta 33 problemas de física sobre vectores. Los problemas involucran determinar el módulo de vectores resultantes dados los módulos y ángulos de otros vectores, calcular ángulos dados información sobre vectores resultantes, y expresar distancias en términos de lados de figuras geométricas regulares usando propiedades de vectores.

1. FÍSICA VECTORES 1
1.En la figura mostrada, determine le módulo del vector resultante.
y
40° 50u
x
170°
30u
A) 20 B) 70 C) 80 D) 100 E) N.A.
2.En la figura mostrada, determine le módulo del vector resultante.
A=5
B=3
85° 25°
O1 O2
A) 14 B) 7 C) 13 D) 12 E) 15
3.En la figura mostrada el módulo de los vectores son A = 10 y B = 12. Si la medida del ángulo es 8 = 60°,
determine le módulo del vector diferencia D.
A D
θ
B
A) 10 B) 11 C) 12 D) 13 E) 14
4.En la figura mostrada el módulo de los vectores son a = 5 y b = 6. Determine el módulo del vector: a – b
a
b
83° 30°
O1 O2
A) 5 B) 6 C) 7 D) 8 E) 4
5.En la figura mostrada el módulo de los vectores son a = 5 y b = 3. Determine el módulo del vector: a – 2b
a
b
63° 10°
A) 5 B) 6 C) 7 D) 8 E) N.A.
6.En la figura mostrada el módulo de los vectores son A = 50 y B = 14. Determine el módulo del vector: A –
B.
A
B
56° 50°
A) 24 B) 48 C) 36 D) 64 E) 42
7.El módulo de la resultante de dos vectores varía entre un valor mínimo de 4 unidades y un valor máximo de
16 unidades. Determine el módulo de la resultante cuando los vectores formen un ángulo de 60°.
A) 14 B) 7 C) 10 D) 12 E) 13
8.El módulo de la resultante de dos vectores varía entre un valor mínimo de 6 unidades y un valor máximo de
24 unidades. Determine el módulo de la resultante cuando los vectores formen un ángulo de 60°.
A) 14 B) 21 C) 20 D) 22 E) 23
Profesor: Dr. Segundo Morocho C. Página 1

2. FÍSICA VECTORES 1
9.La figura muestra dos vectores un de módulo 60 unidades y el otro de módulo variable. Determine la
resultante mínima que se puede conseguir.
B
143°
A=60
A) 12 B) 24 C) 36 D) 48 E) 60
10.Se muestra tres vectores. Determine el módulo del vector resultante.
4u
5u
67°
O 3u
A) 12 B) 2 C) 3 D) 8 E) N.A.
11.Se muestra tres vectores. Determine el módulo del vector resultante.
3 2
6
75°
3 2
O
A) 2 B) 4 C) 6 D) 8 E) N.A.
12.Se muestra tres vectores, donde A = 5, B = 3 y C = 8. Determine el módulo del vector resultante.
A
C 60° B
A) 0 B) 5 C) 10 D) 12 E) N.A.
13.Determine el módulo de la resultante de dos vectores cuyos módulos son 15 y 7 unidades, si forman un
ángulo de 53º.
A) 32 B) 28 C) 20 D) 40 E) 30
14.Se muestra una cuadricula donde el lado de cada cuadrado es 3 u. Determine el módulo del vector
resultante.
A B
C
A) 2u B) 3u C) 4u D) 5u E) 30
15.En el sistema vectorial mostrado, determine el módulo del vector resultante.
b
c
a
1
A) 0 B) 3 C) 5 D) 6 E) 7
Profesor: Dr. Segundo Morocho C. Página 2

3. FÍSICA VECTORES 1
16.En el sistema vectorial mostrado, determine el módulo del vector resultante.
1
1
A) 13 B) 14 C) 15 D) 16 E) 10
17.En el sistema vectorial mostrado, determine el módulo del vector resultante.
1
A) 1 B) 2 C) 3 D) 4 E) 10
18.En el sistema vectorial mostrado, determine el módulo del vector resultante.
b a
c d
1
A) 1 B) 2 C) 3 D) 4 E) N.A.
19.Se muestra un trapecio de vértices A, B, C y D. Si M es punto medio de AB y además BC = 5 cm y AD = 7
cm determine el módulo del vector resultante.
B C
a
M
b
A D
A) 10 cm B) 12 cm C) 14 cm D) 16 cm E) 18 cm
20.Sabiendo que AP = 12, PC = 4 y PB = 3. Determine el módulo del vector resultante.
B
A P C
A) 10 B) 12 C) 14 D) 16 E) N.A.
21.Sabiendo que AB = 12, BC = 4 y PB = 2. Determine el módulo del vector resultante.
D
A B C
A) 10 B) 12 C) 14 D) 16 E) N.A.
22.Se muestra un cubo de arista 2 cm. Determine el módulo del vector resultante.
Profesor: Dr. Segundo Morocho C. Página 3

4. FÍSICA VECTORES 1
A) 1 cm B) 2 cm C) 4 cm D) 6 cm E) N.A.
23.Se muestra un cubo de arista 2 cm. Determine el módulo del vector resultante.
A) 8 cm B) 2 cm C) 4 cm D) 6 cm E) N.A.
24.Determine el módulo de la resultante.
 
b a
82º a = 10, b = 4 2 y c = 10
135º

c
A) 2 B) 3 C) 3 D) 2 2 E) 6
25.Si la resultante de los vectores es nula, determine la medida del ángulo θ.

A

C θ A = 5, B = 3, C = 7

B
A) 45º B) 30º C) 90º D) 53º E) 60º
26.El la figura mostrada determine el módulo del vector resultante.
y
10
6 53°
x
8
A) 5 B) 7 C) 8 D) 9 E) 0
27.Determine la medida del ángulo  tal que, el vector resultante tiene dirección horizontal.
y 20
15 θ
0 x
20
A) 60° B) 45° C) 37° D) 53° E) 90°
Profesor: Dr. Segundo Morocho C. Página 4

5. FÍSICA VECTORES 1
28.Determine la medida del ángulo o  tal que, la resultante de los vectores sea nula.
y
F
12 θ
0 x
9
A) 60° B) 45° C) 37° D) 53° E) 90°
29.La figura muestra un hexágono regular. Determinar “x” en función de a y b.
A) (4a + 3b)/2 B) (2a + b)/5 C) (a + b)/2 D) (4a - 3b)/2 E) Ninguna anterior
B C B C
a a
A D A D
x
x
b b
F E F E
Para el problema 29 Para el problema 30
30.La figura muestra un hexágono regular de vértices A, B, C, D, E y F. Determinar “x” en función de a y b.
A) (4a + 3b)/2 B) (2a + b)/5 C) (a + b)/2 D) (4a - 3b)/2 E) Ninguna anterior
B C
A D
F E
Para el problema 31
C
B C
a x
M
x
b G
A D
Para el problema 32 A
B
y
Profesor: Dr. Segundo Morocho C. Para el problema 33 Página 5

6. FÍSICA VECTORES 1
31.Si ABCDEF son los vértice de un hexágono regular de lado igual a 6 cm. Determine el módulo del vector
resultante.
A) L 3 B) 2L 3 C) 3L 3 D) 5L 3 cm E) ninguna anterior
32.Si A, B, C y D es un paralelogramo y M es punto medio de AB, determinar el vector “x” en función de a y
b.
A) (a - b)/3 B) (2a + b)/5 C) (a + b)/2 D) (4a - 3b)/2 E) Ninguna anterior
33.La figura muestra un triangulo rectángulo isósceles recto en B, donde G es el baricentro, y donde los
  
vectores cumplen la siguiente relación: y + 3 x = 8 2 cm . Calcular el modulo de vector y .
A) 5 cm B) 4 cm C) 3 cm D) 2 cm E) 1 cm
Profesor: Dr. Segundo Morocho C. Página 6