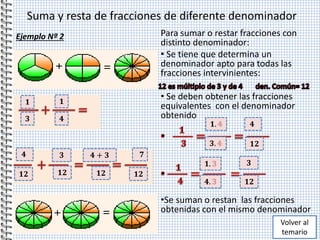
El documento aborda las fracciones y su operación, incluyendo reducción a un común denominador, suma, resta, multiplicación y división. Se describen métodos para trabajar con fracciones de igual y diferente denominador, así como problemas prácticos para aplicar los conceptos. También se trata la resolución de problemas que involucran operaciones con fracciones en contextos de la vida diaria.

1. Temario
 Reducción de fracciones a común denominador
A través de familia de fracciones equivalentes
Determinando el múltiplo común
 Suma y resta
 Suma y resta de fracciones de igual denominador
 Suma y resta de diferente denominador
 Primer Método (familia de fracciones equivalentes)
 Segundo Método ( determinando el denominador común)
 Sumar o resta una fracción con un número entero
 Resolución de problemas
 Multiplicación
 Multiplicación de un entero por una fracción
 Calcular parte de un entero
 Multiplicación de dos o más fracciones
 División
División utilizando el inverso multiplicativo
 División con producto cruzados
 Problemas resueltos 1
 2

2. Reducción de fracciones a común denominador
• Dadas dos o más fracciones. Obtenemos la familia de fracciones
equivalentes multiplicando numerador y denominador por el
mismo número
=
4
6
=
6
9
=
8
12
=
10
15
=
10
12
=
15
18
=
20
24
=
25
30
=
2
8
=
3
12
=
4
16
=
5
20
Los denominadores son múltiplos de 3
Los denominadores son múltiplos de 4
Los denominadores son múltiplos de 6
x 2
x 3
x 4
x 5
• Por lo tanto el Denominador Común resulta ser 12 que es múltiplo
menor de todo los denominadores
2
3
=
2 . 𝟒
3 . 𝟒
=
8
12
1
4
=
1 . 𝟑
4 . 𝟑
=
3
12
5
6
=
5 . 𝟐
6 , 𝟐
=
10
12
2
3
1
4
5
6
Volver al
temario

3. Reducción de fracciones a común denominador
• Dadas las fracciones
2
5
,
7
10
y
3
4
• Elegimos el denominador común entre los múltiplos del mayor
denominador
• múltiplos de 10 = 10, 20, 30, 40
• Entre estos hay que determinar cual es múltiplo de los demás
denominadores
• 10 = 10, 20, 30, 40
• Luego se obtienen las fracciones equivalentes con del den. Com.
No es múltiplo de 4
El Denominador común es = 20 por ser múltiplo de
4, 5 y 10
Volver al
temario
Resolver
ejercicios

4. Suma y resta de fracciones de igual
denominador
𝟏𝟎
𝟓 𝟕 𝟑 𝟏𝟓
𝟏𝟎
𝟓
𝟏𝟐 𝟏𝟓 𝟖 𝟏𝟗
𝟓
Volver al
temario
Cuando se suman o restan dos o más fracciones que tienen el mismo denominador , el
resultado es una fracción del mismo denominador y el numerador es igual la suma o resta
de los denominadores

5. Suma y resta de fracciones de diferente denominador
Para sumar o restar fracciones con
distinto denominador:
• Obtener la familia de fracciones
equivalentes de cada uno de los
términos
•
•Se elije las fracciones con el el mismo
denominador
•Se suman o restan las fracciones
obtenidas con el mismo denominador
𝟒
𝟏 𝟐
𝟓
𝟏𝟎
𝟐𝟎
𝟒 𝟔
𝟐𝟎
𝟓
𝟐
𝟐𝟓
𝟐𝟎
𝟖
𝟐𝟎
𝟓 + 𝟖
Ejemplo Nª 1
𝟖
𝟑
𝟏𝟐
𝟒
𝟏𝟔
𝟓
𝟐𝟎
𝟏𝟎 𝟏𝟓
𝟖
𝟐𝟎
𝟏𝟑
Volver al
temario

6. Suma y resta de fracciones de diferente denominador
Para sumar o restar fracciones con
distinto denominador:
• Se tiene que determina un
denominador apto para todas las
fracciones intervinientes:
• Se deben obtener las fracciones
equivalentes con el denominador
obtenido
•Se suman o restan las fracciones
obtenidas con el mismo denominador
𝟑
𝟏 𝟏
𝟒
𝟏𝟐𝟑.
𝟏. 𝟒
𝟏𝟐
𝟒
𝟏𝟐𝟒.
𝟏. 𝟑
𝟏𝟐
𝟑
𝟏𝟐
𝟒 + 𝟑
Ejemplo Nª 2
𝟏𝟐
𝟕
Volver al
temario

7. Sumar o resta una fracción con un número
entero
• Una pintora tiene terminados dos cuadros y la cuarta parte
de otro Cuanto pintó:
Ejemplos
3 +
2
5
=
3 .𝟓
1 .𝟓
+
2
5
=
15+2
5
=
17
5
2 −
7
10
=
2 .10
1 .10
−
7
10
=
20+7
10
=
27
10
Volver al
temario

8. RESOLUCIÓN
Juan tiene que leerse un libro en tres día. El 1er día leyó
la mitad , el 2do la tercera parte ¿cuánto tendrá que leer
el 3er día para completar el libro?
1er día 2er día
1
2
1
3
3
6
2
6
+
+
=
3 + 2
6
=
5
6
Juan leyó
5
6
Le falta = total − lo que leyó
1 −
5
6
=
Leyó
6
6
−
5
6
=
6 −1
6
=
1
6
RESPUESTA A juan le falta
1
6Volver al
temario

9. Multiplicación de un entero por una fracción
• Juan en cuatro oportunidades contestó 2 tercios de las preguntas, o
sea que en total contestó:
• 4 veces
2
3
=
2
3
+
2
3
+
2
3
+
2
3
=
2+2+2+2
3
=
4 . 2
3
=
8
3
Ejemplos:
• 5 .
3
10
=
5 . 3
10
=
15
10
=
𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑛𝑑𝑜
=
3
2
• 2 .
5
7
=
2 . 5
7
=
10
7
• 6 .
4
15
=
6 . 4
15
=
24
15
=
𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑛𝑑𝑜
=
8
5
Volver al
temario

10. Calcular la fracción de un número
En un depósito en Caja de Ahorro hay $ 5610 y le permiten extraer solo las dos
terceras partes. Calcular cuanto dinero retiraran
Una pieza de tela tiene 120m de seda y una costurera le encargó
las tres cuartas partes. ¿Cuántos metros se llevó?
𝑙𝑙𝑒𝑣ó
3
4
𝑑𝑒 120𝑚 =
3 ∙ 120𝑚
4
= 90𝑚
 Se vendieron los
2
5
de las 15 flores que tenía
Volver al
temario
6
5
15.2
5
15
veces2 
𝑡𝑜𝑡𝑎𝑙 𝑑𝑒𝑙 𝑑𝑒𝑝ó𝑠𝑖𝑡𝑜
2
3
𝑑𝑒 $ 5610 =
2 ∙$ 5610
3
= $ 3740
1
3
𝑑𝑒 $ 5610 =
$ 5610
3
= $1870

11. Multiplicación de dos fracciones
Ejemplo 1 : edificar en las
3
4
de los
2
5
que está desmalezado
de los
2
5
, se toman solo las
3
4
=
3
4
de
2
5
=
6
20
3
4
.
2
5
=
3 .2
4 ,5
=
6
20
→ 𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑛𝑑𝑜 =
3
10
El PRODUCTO DE DOS FRACCIONES es una fracción:
Cuyo numerador es igual al producto de los numeradores
Y el Denominador es igual al producto de los denominadores
𝑎
𝑏
.
𝑐
𝑑
=
𝑎.𝑐
𝑏.𝑑
Ejemplos y Ejercicios
2
5
el total
3
4
𝑝𝑎𝑟𝑡𝑒𝑠 𝑑𝑒
2
5

12. Multiplicar dos o más Fracciones
𝟏𝟐
𝟖
𝟏𝟓
𝟐𝟓
𝟏𝟐 . 𝟏𝟓
𝟐𝟓 . 𝟖
4.3
4.2
5.3
5.5
𝟗
10
𝟏𝟖
9
𝟏𝟒
𝟏𝟐
𝟐𝟔
𝟏𝟓
𝟏𝟒
𝟐𝟏
𝟑𝟐
2𝟒
𝟒𝟗
𝟕
𝟑𝟓
𝟒𝟐
𝟑𝟔
𝟗 Volver al
temario

13. Volver al
temario
División
• Recuerdas: “Todo número dividido por sí mismo de 1 ”
• 8 ∶ 8 = 1 17 ∶ 17 = 1 257 ∶ 257 = 1
• Entonces
2
3
∶
2
3
= 1 𝑦
2
3
3
2
= 1
• “Dividir por un número es equivalente a multiplicar por su
inverso multiplicativo”
•
Inversos de la
multiplicación
𝟓 𝟑
7𝟔
𝟓
𝟔
7
𝟑
𝟑𝟓
𝟏𝟖

14. Otra técnica para dividir fracciones
7
5
∶
11
2
=
7
5
∙
2
11
=
→
7
5
∶
11
2
=
7 ∗ 2
5 ∗11
14
55
El cociente de las dos fracciones se obtiene como cociente
de los productos cruzados
Volver al
temario
Para hallar el cociente de dos fracciones, vimos que: se multiplica
por la fracción inversa de la segunda.

15. Resolución de problemas
• Un artesano emplea la tercera parte de una pieza de cuero para
confeccionar un par de ojotas, ¿Cuánto emplea para una ojota?
• Si para 2 ojotas es necesario
1
3
de la pieza de cuero, para una sola
ojota hace falta la mitad
• Simbólicamente: la
1
2
𝑑𝑒
1
3
=
1
2
∙
1
3
=
1
3
𝑝𝑎𝑟𝑎 Para una ∶ la
1
2
𝑑𝑒
1
3
1
6
𝑑𝑒𝑙 𝑡𝑜𝑡𝑎𝑙
Respuesta: el artesano necesitaá
1
6
𝑑𝑒𝑙 𝑡𝑜𝑡𝑎𝑙
1
6
Volver al
temario

16. Para pensar, plantear y resolver
• Si hay que repartir3
1
2
𝑘𝑔 de helado en potes con una
capacidad de
3
8
𝑘𝑔 ¿Cuántas potes se utilizaran?
•Tengo para repartir
3
4 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎𝑑𝑜
𝑒𝑛 𝑓𝑟𝑎𝑐𝑐𝑖ó𝑛
𝑜𝑟𝑑𝑖𝑛𝑎𝑟𝑖𝑜
.4+3
4
=
15
4
• Es necesario determinar cuantas veces entra
•
3
8
𝑘𝑔 en
15
4
𝑘𝑔 →
• →
15
4
:
3
8
=
=
15
4
∙
8
3
=
Respuesta: con 3
1
2
𝑘𝑔
se llenaran potes

17. Interpretar, plantear y resolver
•Juan tiene que leerse un libro en tres día. El 1er día leyó la mitad
, el 2do la tercera parte ¿cuánto tendrá que leer el 3er día para
completar el libro?
• Un campesino quiere repartir su campo de tal forma que 3
quintas partes se siembren con trigo, la cuarta parte con maíz y
el resto para la granja. ¿Cuál es la par te del campo destinada
para la granja?
• Un panadero preparó dos pasta floras para vender en
porciones, en la mañana vendió 2 tercio y por la tarde 5 o sextos.
¿Cuánto le quedó sin vender?
•En una competencia se realiza las parte del recorrido en
bicicleta, corriendo y el resto nadando ¡Qué parte del recorrido
corresponde a la disciplina natación?

18. Tengo que poner 900 ladrillos en una pared. Hoy pondré ¼ del total. ¿Cuántos
son?.
Si mañana pongo 2/9 de los que me faltan, ¿cuántos pondré?.
¿Cuántos faltaran por poner?
Tengo un campo de 8000 m2. Si hemos sembrado 2/5 de mi campo de cereales y de
estos, ¾ son de trigo, ¿qué superficie tengo sembrada de trigo
Un padre decide repartir 2.100 euros entre sus tres hijos. Al mayor decide darle las
2/5 partes; al siguiente los 3/7, y al menor el resto. ¿Qué cantidad se llevó cada uno?
En una bolsa había 400 canicas, primero saqué 2 /5 de las canicas, es decir, saqué
________ canicas, y en la bolsa quedaron ________. Luego, de las que quedaban
saqué
• 1 /3, es decir, saqué _______ canicas. ¿Cuántas me quedan todavía? __________